3.3.1两条直线的交点坐标
图片预览





文档简介
(共15张PPT)
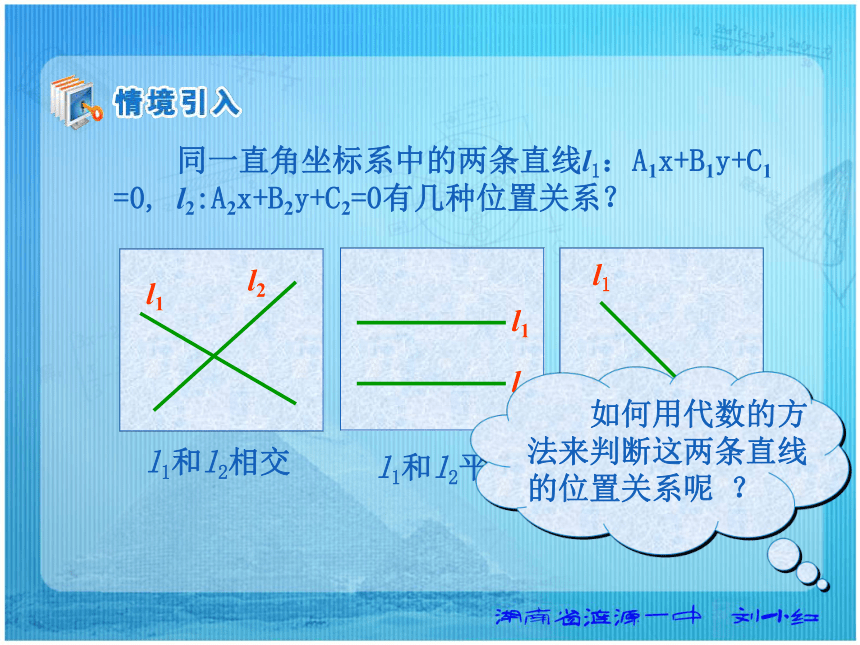
同一直角坐标系中的两条直线l1:A1x+B1y+C1
=0, l2:A2x+B2y+C2=0有几种位置关系?
l1和l2相交
l1
l2
l1
l2
l1
l2
l1和l2平行
l1和l2重合
如何用代数的方
法来判断这两条直线
的位置关系呢 ?
几何元素及关系
代数表示
点A
直线l1
点A在l1直线上
直线l1与l2的交
点是A
下面的表格中,你能用代数表示表示出左边的几何元素及关系吗?
A(a,b)
l1:A1x+B1y+C1=0
A1a+B1b+C1=0
点A的坐标是方程组
的解.
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
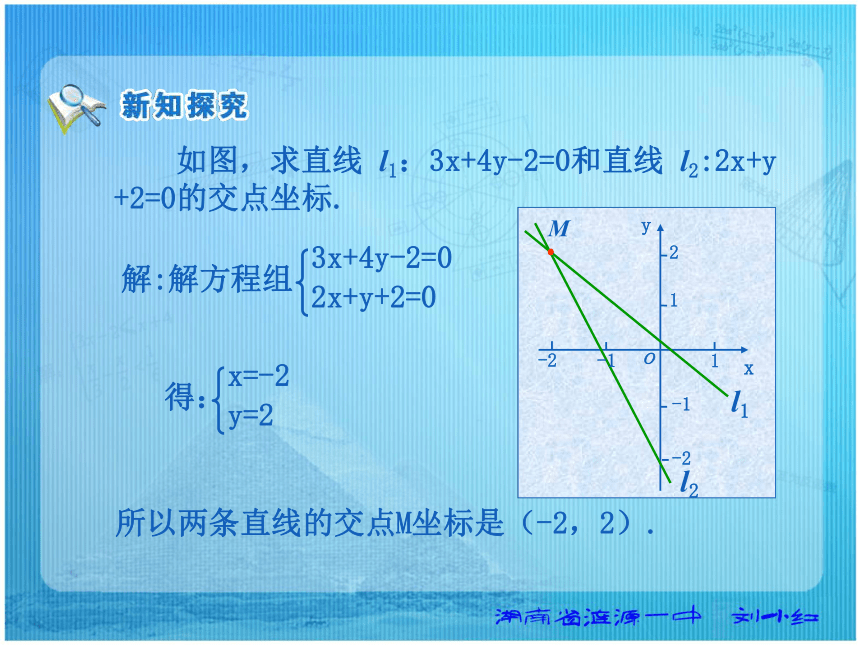
如图,求直线 l1:3x+4y-2=0和直线 l2:2x+y
+2=0的交点坐标.
3x+4y-2=0
2x+y+2=0
x=-2
y=2
解:解方程组
所以两条直线的交点M坐标是(-2,2).
得:
x
y
-2
1
2
M
o
-1
1
-2
-1
l1
l2
二元一次方程组 的解与两直线
和的位置关系有什么关系?
A1x+B1y+C1=0
A2x+B2y+C2=0
(1)若二元一次方程组有唯一解,l1与l2 ,
交点为二元一次方程的解.
(2)若二元一次方程组无解,则l1与l2 ,两
条直线没有公共点 .
(3)若二元一次方程组有无数解,则l1与l2 .
相交
重合
平行
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
x-y=0
3x+3y-10=10
解:
x=
y=
得:
5
3
5
3
所以l1与l2相交,
(1)解方程组
5
3
5
3
交点坐标为( , ).
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
3x-y+4=0
6x-2y-1=0
解:
得出方程组无解,所以两直线无公共点,
即l1与l2平行.
(2)解方程组
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
3x+4y-5=0
6x+8y-10=10
解:
两个方程可以化成同一个方程,因此两个方程表示同一条直线,即l1与l2重合.
(3)解方程组
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
两条直线的交点坐标
求下列各对直线的交点坐标,并画出图形
(1)l1:2x+3y=12, l2:x-2y=4
(2)l1:x=2, l2:3x+2y-12=0
2x+3y-12=0
x-2y-4=0
得:
x=
y=
36
7
4
7
所以直线l1与l2的交点坐标是( , ).
36
7
4
7
解:
(1)解方程组
求下列各对直线的交点坐标,并画出图形
x-2=0
3x+2y-12=0
所以直线l1与l2的交点坐标是(2,3).
得:
x=2
y=3
解:
(2)解方程组
(1)l1:2x+3y=12, l2:x-2y=4
(2)l1:x=2, l2:3x+2y-12=0
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:2x-3y=7, l2:4x+2y=1
解:
所以l1与l2相交,
得:
x=
y=
17
16
13
8
-
2x-3y-7=0
4x+2y-1=0
(3)l1( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
(1)将方程变形后,解方程组
17
16
13
8
-
交点坐标为( , ).
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
将直线l1的方程变形后可以发现, l1的方程可以化成直线l2
的方程.所以直线l1与l2表示同一条直线,即直线与重合.
2x-6y+4=0
X-3y+2=0
解:
(2)将方程变形后,解方程组
(1)l1:2x-3y=7, l2:4x+2y=1
(3)l1:( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
得出方程组无解.
所以直线l1与l2没有公共点,即直线l1与l2平行.
( -1)x+y-3=0
2
x+( +1)y-2=0
2
解:
(3)将方程变形后,解方程组
(1)l1:2x-3y=7, l2:4x+2y=1
(3)l1:( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
x
y
o
M
P
光线从M(-2,3)射到x轴上的一点P(1,0)后
被x轴反射,求反射光线所在的直线方程.
▲
▲
同一直角坐标系中的两条直线l1:A1x+B1y+C1
=0, l2:A2x+B2y+C2=0有几种位置关系?
l1和l2相交
l1
l2
l1
l2
l1
l2
l1和l2平行
l1和l2重合
如何用代数的方
法来判断这两条直线
的位置关系呢 ?
几何元素及关系
代数表示
点A
直线l1
点A在l1直线上
直线l1与l2的交
点是A
下面的表格中,你能用代数表示表示出左边的几何元素及关系吗?
A(a,b)
l1:A1x+B1y+C1=0
A1a+B1b+C1=0
点A的坐标是方程组
的解.
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
如图,求直线 l1:3x+4y-2=0和直线 l2:2x+y
+2=0的交点坐标.
3x+4y-2=0
2x+y+2=0
x=-2
y=2
解:解方程组
所以两条直线的交点M坐标是(-2,2).
得:
x
y
-2
1
2
M
o
-1
1
-2
-1
l1
l2
二元一次方程组 的解与两直线
和的位置关系有什么关系?
A1x+B1y+C1=0
A2x+B2y+C2=0
(1)若二元一次方程组有唯一解,l1与l2 ,
交点为二元一次方程的解.
(2)若二元一次方程组无解,则l1与l2 ,两
条直线没有公共点 .
(3)若二元一次方程组有无数解,则l1与l2 .
相交
重合
平行
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
x-y=0
3x+3y-10=10
解:
x=
y=
得:
5
3
5
3
所以l1与l2相交,
(1)解方程组
5
3
5
3
交点坐标为( , ).
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
3x-y+4=0
6x-2y-1=0
解:
得出方程组无解,所以两直线无公共点,
即l1与l2平行.
(2)解方程组
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
3x+4y-5=0
6x+8y-10=10
解:
两个方程可以化成同一个方程,因此两个方程表示同一条直线,即l1与l2重合.
(3)解方程组
(1)l1:x-y=0, l2:3x+3y-10=10
(2)l1:3x-y+4=0, l2:6x-2y-1=0
(3)l1:3x+4y-5=0, l2:6x+8y-10=10
两条直线的交点坐标
求下列各对直线的交点坐标,并画出图形
(1)l1:2x+3y=12, l2:x-2y=4
(2)l1:x=2, l2:3x+2y-12=0
2x+3y-12=0
x-2y-4=0
得:
x=
y=
36
7
4
7
所以直线l1与l2的交点坐标是( , ).
36
7
4
7
解:
(1)解方程组
求下列各对直线的交点坐标,并画出图形
x-2=0
3x+2y-12=0
所以直线l1与l2的交点坐标是(2,3).
得:
x=2
y=3
解:
(2)解方程组
(1)l1:2x+3y=12, l2:x-2y=4
(2)l1:x=2, l2:3x+2y-12=0
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
(1)l1:2x-3y=7, l2:4x+2y=1
解:
所以l1与l2相交,
得:
x=
y=
17
16
13
8
-
2x-3y-7=0
4x+2y-1=0
(3)l1( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
(1)将方程变形后,解方程组
17
16
13
8
-
交点坐标为( , ).
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
将直线l1的方程变形后可以发现, l1的方程可以化成直线l2
的方程.所以直线l1与l2表示同一条直线,即直线与重合.
2x-6y+4=0
X-3y+2=0
解:
(2)将方程变形后,解方程组
(1)l1:2x-3y=7, l2:4x+2y=1
(3)l1:( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
判断下列各对直线的位置关系.如果相交,求
出交点的坐标
得出方程组无解.
所以直线l1与l2没有公共点,即直线l1与l2平行.
( -1)x+y-3=0
2
x+( +1)y-2=0
2
解:
(3)将方程变形后,解方程组
(1)l1:2x-3y=7, l2:4x+2y=1
(3)l1:( -1)x+y=3, l2:x+( +1)y=2
2
2
(2)l1:2x-6y+4=0, l2:y=
x
3
+
2
3
x
y
o
M
P
光线从M(-2,3)射到x轴上的一点P(1,0)后
被x轴反射,求反射光线所在的直线方程.
▲
▲
