3.3.2两点间的距离
图片预览






文档简介
课件15张PPT。 如图,王明家和学校的位置如图所示:如何能求出王明家到学校的距离? 可否通过建立适当的直角坐标系,然后求出
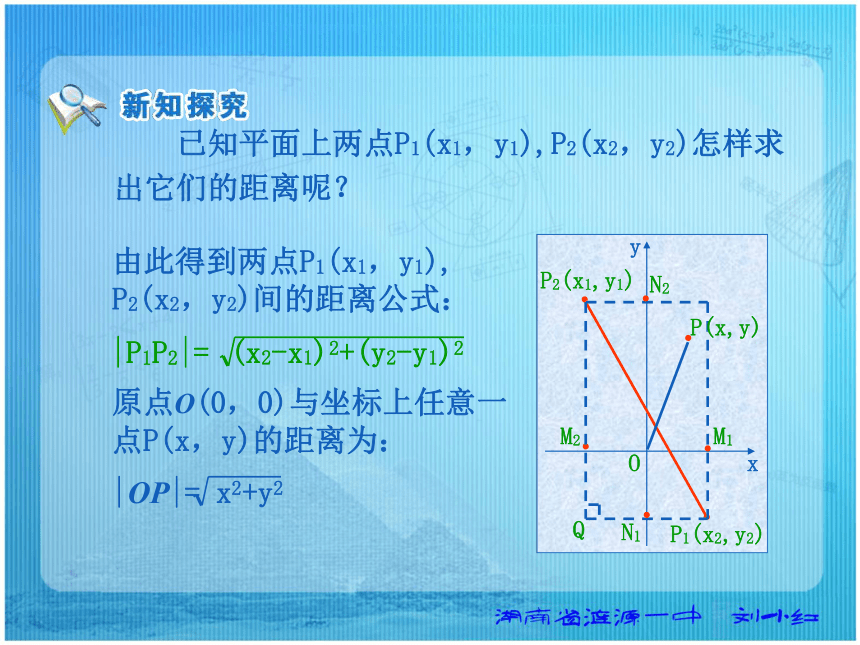
它们的距离? 已知平面上两点P1(x1,y1),P2(x2,y2)怎样求
出它们的距离呢?M2 M1 N1 N2 P1(x2,y2) P2(x1,y1) 在Rt△P1QP2中, |P1P2|2=|P1Q|2+|QP2|2|P1Q|=|M1M2|=|x2-x1| |QP2|=|N1N2|=|y2-y1| 所以|P1P2|2=|x2-x1|2+|y2-y1|2 ...... 已知平面上两点P1(x1,y1),P2(x2,y2)怎样求
出它们的距离呢?M2 M1 N1 N2 P1(x2,y2) P2(x1,y1) 由此得到两点P1(x1,y1),
P2(x2,y2)间的距离公式: ......原点O(0,0)与坐标上任意一
点P(x,y)的距离为:|P1P2|= .P(x,y)解:设所求点为P(x,0),于是有 |PA|= |PB|= 由|PA|=|PB|得 x2+2x+5= 解得x=1. 所以,所求点为P(1,0), |PA|= x2-4x+11,且 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: D(b,c)A(0,0)B(a,0)C(a+b,c)以顶点A为坐标原
点,AB边所在的
直线为x轴建立直
角坐标系,则有
A(0,0). 设B(a,0), D(b,c), 由平行四边形的性质得到C点的坐标为:(a+b,c) 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: 因为:|AB|2+|CD|2+|AD|2+|BC|2=2(a2+b2+c2); D(b,c)A(0,0)B(a,0)C(a+b,c)|AC|2+|BD|2=2(a2+b2+c2); 所以:|AB|2=a2, |CD|2=a2, |AD|2=b2+c2, |BC|2=b2+c2, |AC|2=(a+b)2+c2, |BD|2=(b-a)2+c2, 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: 所以:|AB|2+|CD|2+|AD|2+|BC|2 =|AC|2+|BD|2 因此平行四边形四条边的平方
等于两条对角线的平方和.D(b,c)A(0,0)B(a,0)C(a+b,c)解:求下列两点间的距离.83解: 已知点A(a,-5)与B(0,10)间的距离是17,
求a的值.因为A,B两点间的距离是17,所以|AB|=17,解出:a=±8.解:已知AO是△ABC中BC边的中线,证明:|AB|2+|AC|2
=2(|AO|2+|OC|2)由两点间距离公式得,以O为坐标原点,BC为x轴,
BC的中垂线为y轴,建立如
图所以的坐标系xoy,A(a,b)B(-c,0)C(c,0) 设点
A(a,b),B(-c,0),C(c,0),|OC|=c, |AO|2+|OC|2=a2+b2+c2, ABCOx 燕隼(sun)和红隼是同属于隼形目隼科的鸟类.
它们的体形大小如鸽,形略似燕,身体的形态特
征比较相似.红隼的体形比燕隼略大。通过抽样
测量已知燕隼的平均体长约为31cm,平均翅长约
为25cm.近日在某地发现了两只形似燕隼或红隼
的鸟A和B经测量,知道这两只鸟的体长和翅长分
别为A(32.65cm,25.2cm),B(33.4cm,26.9cm). 你能否设计出一种近似的方法,利用这些数
据判断这两只鸟是燕隼还是红隼?
它们的距离? 已知平面上两点P1(x1,y1),P2(x2,y2)怎样求
出它们的距离呢?M2 M1 N1 N2 P1(x2,y2) P2(x1,y1) 在Rt△P1QP2中, |P1P2|2=|P1Q|2+|QP2|2|P1Q|=|M1M2|=|x2-x1| |QP2|=|N1N2|=|y2-y1| 所以|P1P2|2=|x2-x1|2+|y2-y1|2 ...... 已知平面上两点P1(x1,y1),P2(x2,y2)怎样求
出它们的距离呢?M2 M1 N1 N2 P1(x2,y2) P2(x1,y1) 由此得到两点P1(x1,y1),
P2(x2,y2)间的距离公式: ......原点O(0,0)与坐标上任意一
点P(x,y)的距离为:|P1P2|= .P(x,y)解:设所求点为P(x,0),于是有 |PA|= |PB|= 由|PA|=|PB|得 x2+2x+5= 解得x=1. 所以,所求点为P(1,0), |PA|= x2-4x+11,且 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: D(b,c)A(0,0)B(a,0)C(a+b,c)以顶点A为坐标原
点,AB边所在的
直线为x轴建立直
角坐标系,则有
A(0,0). 设B(a,0), D(b,c), 由平行四边形的性质得到C点的坐标为:(a+b,c) 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: 因为:|AB|2+|CD|2+|AD|2+|BC|2=2(a2+b2+c2); D(b,c)A(0,0)B(a,0)C(a+b,c)|AC|2+|BD|2=2(a2+b2+c2); 所以:|AB|2=a2, |CD|2=a2, |AD|2=b2+c2, |BC|2=b2+c2, |AC|2=(a+b)2+c2, |BD|2=(b-a)2+c2, 证明平行四边形四条边的平方和等于两条对
角线的平方和.证明: 所以:|AB|2+|CD|2+|AD|2+|BC|2 =|AC|2+|BD|2 因此平行四边形四条边的平方
等于两条对角线的平方和.D(b,c)A(0,0)B(a,0)C(a+b,c)解:求下列两点间的距离.83解: 已知点A(a,-5)与B(0,10)间的距离是17,
求a的值.因为A,B两点间的距离是17,所以|AB|=17,解出:a=±8.解:已知AO是△ABC中BC边的中线,证明:|AB|2+|AC|2
=2(|AO|2+|OC|2)由两点间距离公式得,以O为坐标原点,BC为x轴,
BC的中垂线为y轴,建立如
图所以的坐标系xoy,A(a,b)B(-c,0)C(c,0) 设点
A(a,b),B(-c,0),C(c,0),|OC|=c, |AO|2+|OC|2=a2+b2+c2, ABCOx 燕隼(sun)和红隼是同属于隼形目隼科的鸟类.
它们的体形大小如鸽,形略似燕,身体的形态特
征比较相似.红隼的体形比燕隼略大。通过抽样
测量已知燕隼的平均体长约为31cm,平均翅长约
为25cm.近日在某地发现了两只形似燕隼或红隼
的鸟A和B经测量,知道这两只鸟的体长和翅长分
别为A(32.65cm,25.2cm),B(33.4cm,26.9cm). 你能否设计出一种近似的方法,利用这些数
据判断这两只鸟是燕隼还是红隼?
