3.3.3-4点到直线的距离、两条平行直线间的距离
文档属性
| 名称 | 3.3.3-4点到直线的距离、两条平行直线间的距离 |  | |
| 格式 | rar | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-09 19:49:00 | ||
图片预览

文档简介
课件18张PPT。 邮电局的旁边是一条国道,那从邮电局到国道的最短距离是多少?设邮电局在平面中的坐标为P0(x0,y0),国道所
在直线的方程为:Ax+By+C=0,如何求出点到直
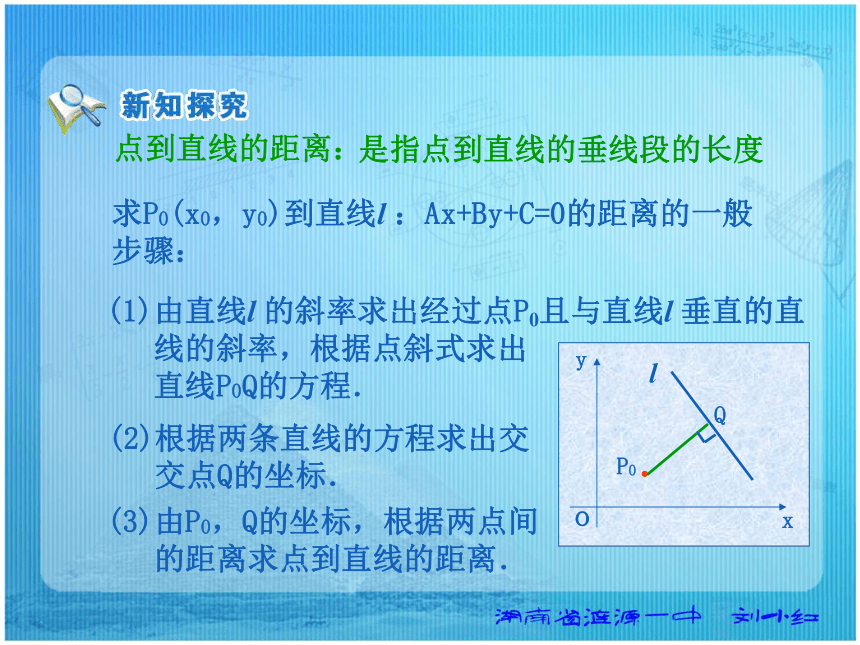
线的距离? 点到直线的距离: 是指点到直线的垂线段的长度 求P0(x0,y0)到直线l :Ax+By+C=0的距离的一般
步骤: (1)由直线l 的斜率求出经过点P0且与直线l 垂直的直
线的斜率,根据点斜式求出
直线P0Q的方程. (2)根据两条直线的方程求出交
交点Q的坐标.(3)由P0,Q的坐标,根据两点间
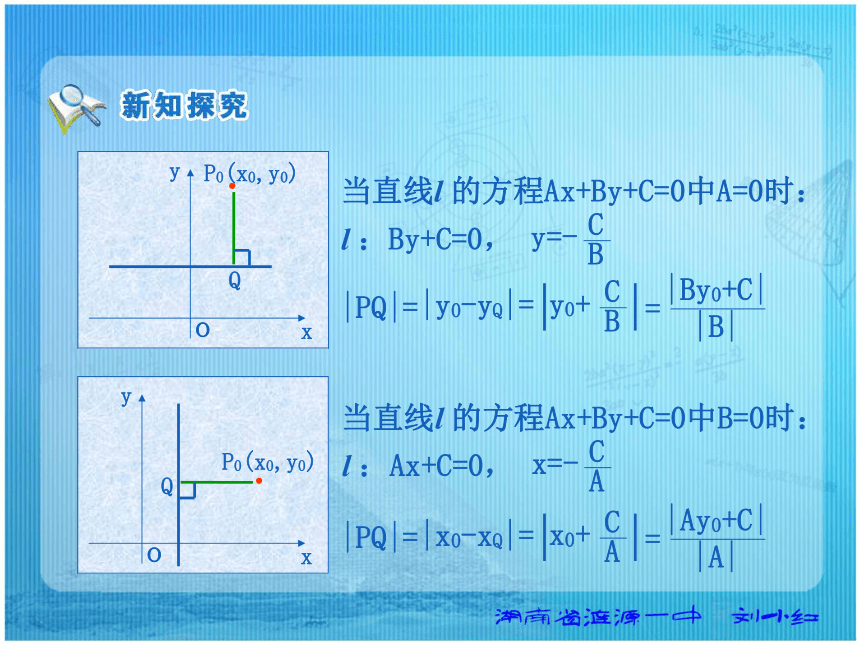
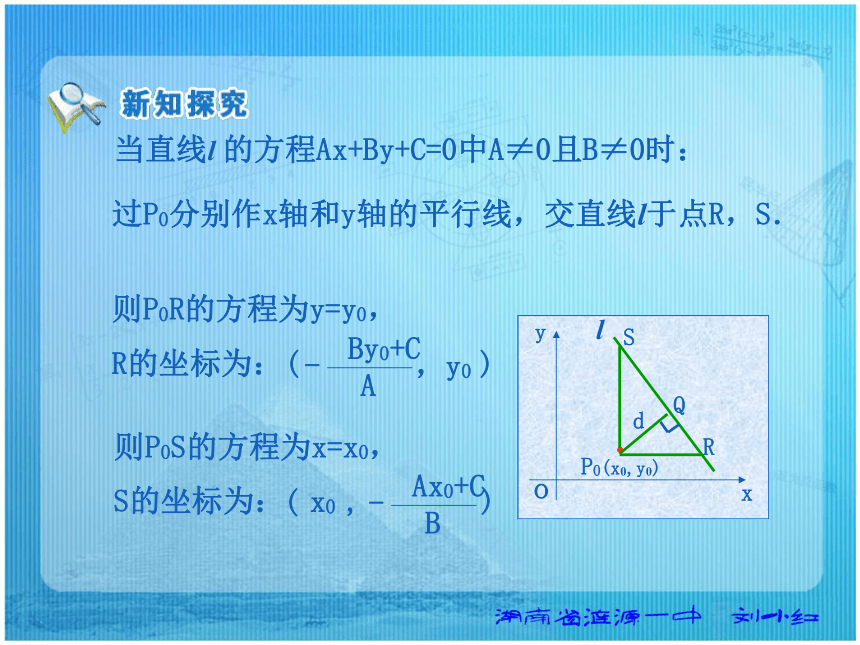
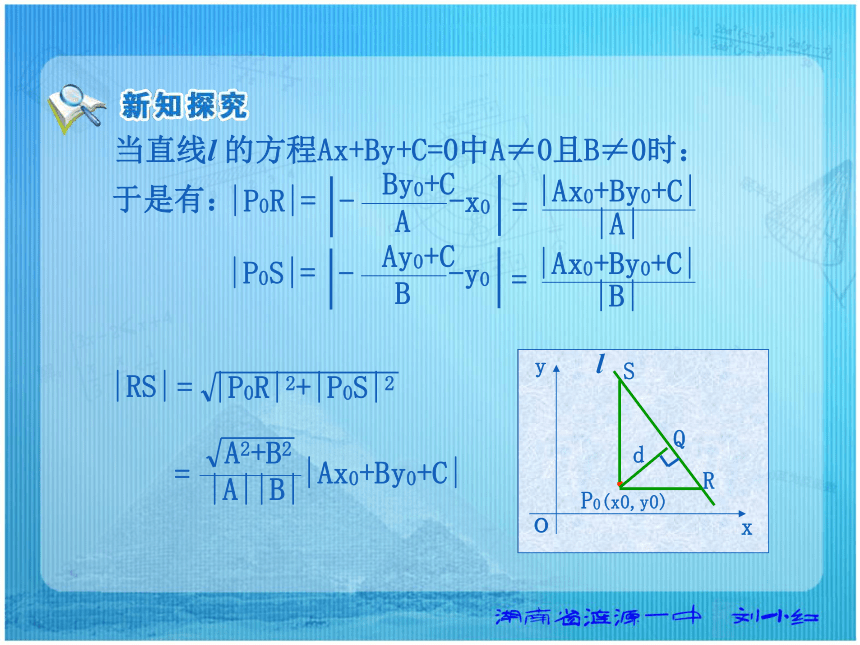
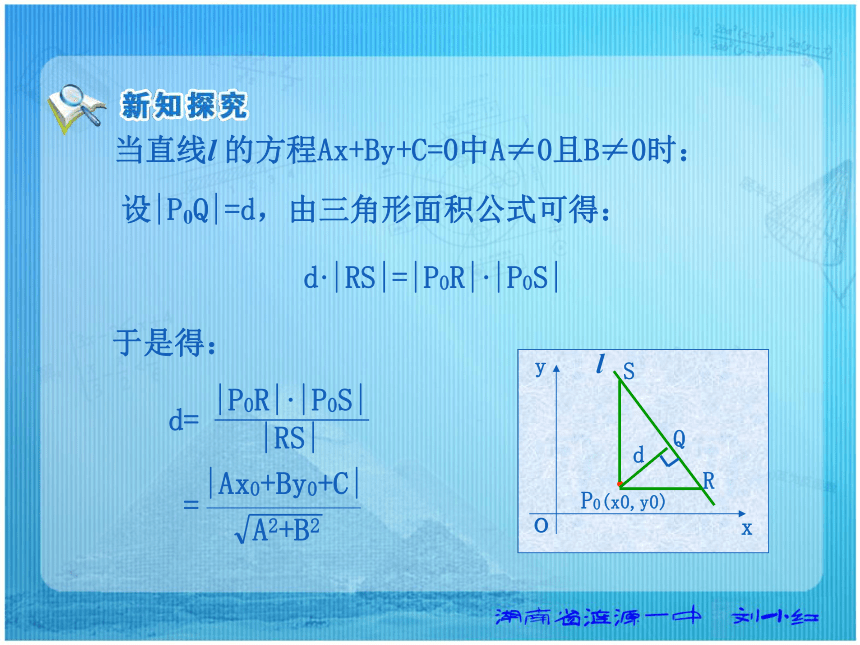
的距离求点到直线的距离.当直线l 的方程Ax+By+C=0中A=0时:l :By+C=0, |y0-yQ|= 当直线l 的方程Ax+By+C=0中B=0时:l :Ax+C=0, |PQ|= |x0-xQ|= |PQ|= 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR过P0分别作x轴和y轴的平行线,交直线l于点R,S.则P0R的方程为y=y0, R的坐标为: 则P0S的方程为x=x0, S的坐标为: 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR于是有:|P0R|= |P0S|= 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR设|P0Q|=d,由三角形面积公式可得:d·|RS|=|P0R|·|P0S|于是得:点P0(x0,y0)到直线l :Ax+By+C=0的距离公式:当直线方程中的A=0时: 当直线方程中的B=0时: 点P0(x0,y0)到直线l :Ax+By+C=0的距离公式:求点(-1,2)到直线:3x=2的距离? 解: 已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.解:设AB边上的高为h, AB边所在的直线方程: 点C到x+y-4=0的距离: h|AB|= 即x+y-4=0。=5 已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.MN解: 延长AB交x轴于点D。D过A,B两点分别作x轴的垂线,垂足为M,N。思考:如何求两条平行直线的距离?探究:能否将两条平行直线间的距离转化为点到
直线的距离?如何取点呢? 两条平行直线间的距离是指夹在两条平行直线间公垂线段的长. 已知直线l1 :2x-7y-8=0,l2 :6x-21y-1=0,求直线l1 与l2 间的距离. 解:设l1 与x轴的交点为A, A点的坐标为:(4,0) 根据点到直线的距离公式:点A到l2 的距离为d= A(4,0).求下列点到直线的距离:(1)A(-2,3),l:3x+4y+3=0 (3)C(1,-2),l: 4x+3y=0 解:d= (1)d= =0(2)d= (3)(1)已知点A(-2,3)到直线y=ax+1的距离为1,求a的值.(2)已知点A(-2,3)到直线y=-x+a的距离为1,求a的值.解: (1)直线方程y=ax+1即ax-y+1=0 d= =1(2)直线方程y=-x+a即x+y-a=0 d= 求下列两条平行线间的距离:(1)2x+3y-8=0,2x+3y+18=0 (2)3x+4y=10,3x+4y=0 (1)直线2x+3y-8=0与x轴的交点A的坐标为:
(4,0).则点A到直线2x+3y+18=0的距离解: d= 求下列两条平行线间的距离:(1)2x+3y-8=0,2x+3y+18=0 (2)3x+4y=10,3x+4y=0 (2)直线3x+4y=0与y轴的交点A的坐标为:(0,0).则点A到直线3x+4y=0的距离解: d= 某市现有自市中心O通向正西和东北方向的
两条主要公路,为了解决交通拥挤问题,市政府
决定修一条环城路,分别在通往正西和东北方向
的公路上选取A、B两点,使环城公路在A、B间为
线段,要求AB环城路段与中心O的距离为10km,
且使A、B间的距离最小,请你确定A、B两点的最
佳位置.
在直线的方程为:Ax+By+C=0,如何求出点到直
线的距离? 点到直线的距离: 是指点到直线的垂线段的长度 求P0(x0,y0)到直线l :Ax+By+C=0的距离的一般
步骤: (1)由直线l 的斜率求出经过点P0且与直线l 垂直的直
线的斜率,根据点斜式求出
直线P0Q的方程. (2)根据两条直线的方程求出交
交点Q的坐标.(3)由P0,Q的坐标,根据两点间
的距离求点到直线的距离.当直线l 的方程Ax+By+C=0中A=0时:l :By+C=0, |y0-yQ|= 当直线l 的方程Ax+By+C=0中B=0时:l :Ax+C=0, |PQ|= |x0-xQ|= |PQ|= 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR过P0分别作x轴和y轴的平行线,交直线l于点R,S.则P0R的方程为y=y0, R的坐标为: 则P0S的方程为x=x0, S的坐标为: 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR于是有:|P0R|= |P0S|= 当直线l 的方程Ax+By+C=0中A≠0且B≠0时:SR设|P0Q|=d,由三角形面积公式可得:d·|RS|=|P0R|·|P0S|于是得:点P0(x0,y0)到直线l :Ax+By+C=0的距离公式:当直线方程中的A=0时: 当直线方程中的B=0时: 点P0(x0,y0)到直线l :Ax+By+C=0的距离公式:求点(-1,2)到直线:3x=2的距离? 解: 已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.解:设AB边上的高为h, AB边所在的直线方程: 点C到x+y-4=0的距离: h|AB|= 即x+y-4=0。=5 已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.MN解: 延长AB交x轴于点D。D过A,B两点分别作x轴的垂线,垂足为M,N。思考:如何求两条平行直线的距离?探究:能否将两条平行直线间的距离转化为点到
直线的距离?如何取点呢? 两条平行直线间的距离是指夹在两条平行直线间公垂线段的长. 已知直线l1 :2x-7y-8=0,l2 :6x-21y-1=0,求直线l1 与l2 间的距离. 解:设l1 与x轴的交点为A, A点的坐标为:(4,0) 根据点到直线的距离公式:点A到l2 的距离为d= A(4,0).求下列点到直线的距离:(1)A(-2,3),l:3x+4y+3=0 (3)C(1,-2),l: 4x+3y=0 解:d= (1)d= =0(2)d= (3)(1)已知点A(-2,3)到直线y=ax+1的距离为1,求a的值.(2)已知点A(-2,3)到直线y=-x+a的距离为1,求a的值.解: (1)直线方程y=ax+1即ax-y+1=0 d= =1(2)直线方程y=-x+a即x+y-a=0 d= 求下列两条平行线间的距离:(1)2x+3y-8=0,2x+3y+18=0 (2)3x+4y=10,3x+4y=0 (1)直线2x+3y-8=0与x轴的交点A的坐标为:
(4,0).则点A到直线2x+3y+18=0的距离解: d= 求下列两条平行线间的距离:(1)2x+3y-8=0,2x+3y+18=0 (2)3x+4y=10,3x+4y=0 (2)直线3x+4y=0与y轴的交点A的坐标为:(0,0).则点A到直线3x+4y=0的距离解: d= 某市现有自市中心O通向正西和东北方向的
两条主要公路,为了解决交通拥挤问题,市政府
决定修一条环城路,分别在通往正西和东北方向
的公路上选取A、B两点,使环城公路在A、B间为
线段,要求AB环城路段与中心O的距离为10km,
且使A、B间的距离最小,请你确定A、B两点的最
佳位置.
