3.1.2两条直线平行与垂直的判定
文档属性
| 名称 | 3.1.2两条直线平行与垂直的判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-09 00:00:00 | ||
图片预览


文档简介
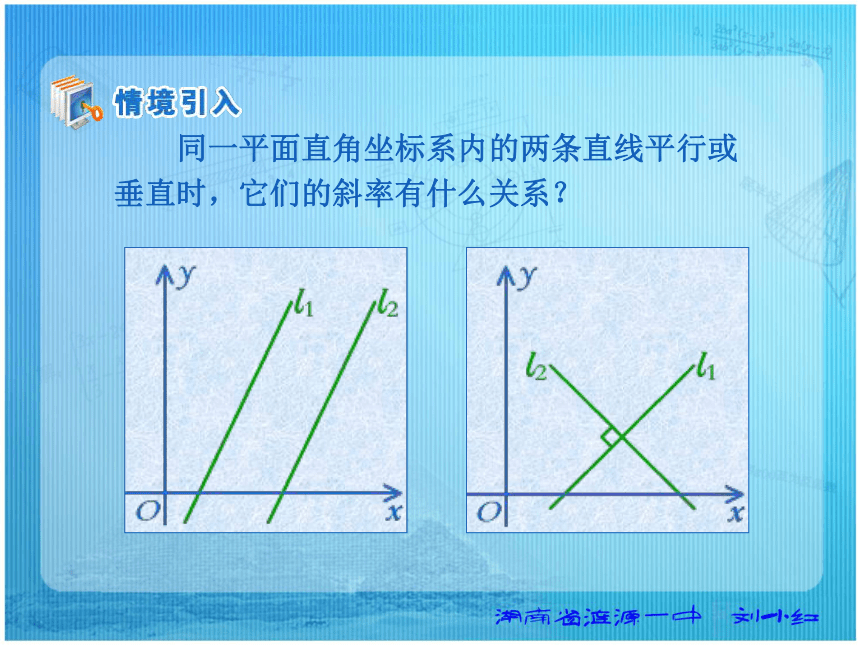
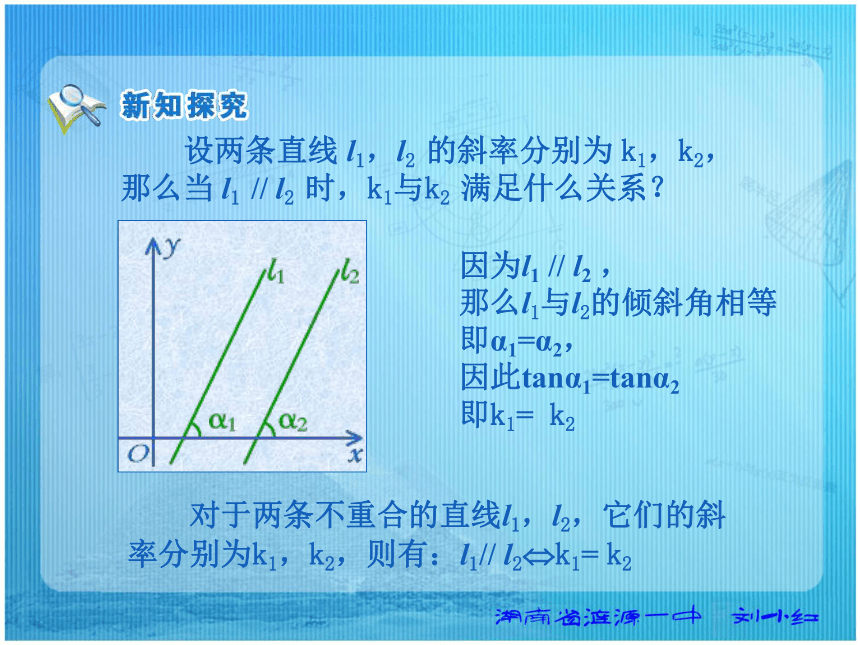
课件19张PPT。 同一平面直角坐标系内的两条直线平行或垂直时,它们的斜率有什么关系? 设两条直线 l1,l2 的斜率分别为 k1,k2,那么当 l1 // l2 时,k1与k2 满足什么关系?因为l1 // l2 ,
那么l1与l2的倾斜角相等
即α1=α2,
因此tanα1=tanα2
即k1= k2 对于两条不重合的直线l1,l2,它们的斜率分别为k1,k2,则有:l1// l2?k1= k2 对于同一平面内两条直线 l1,l2,
它们的斜率分别为 k1,k2,有
k1= k2 ? l1 // l2或 l1 与 l2 重合.
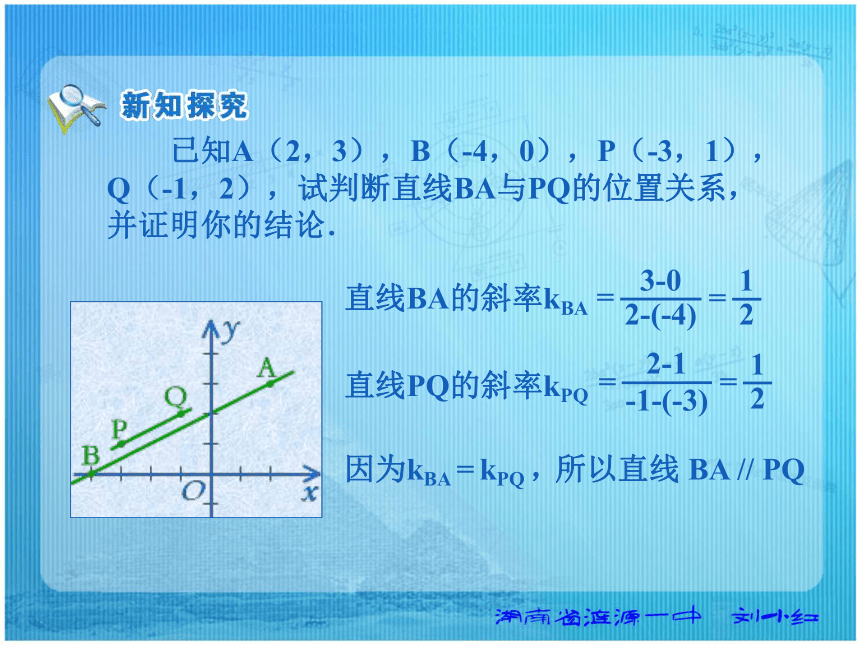
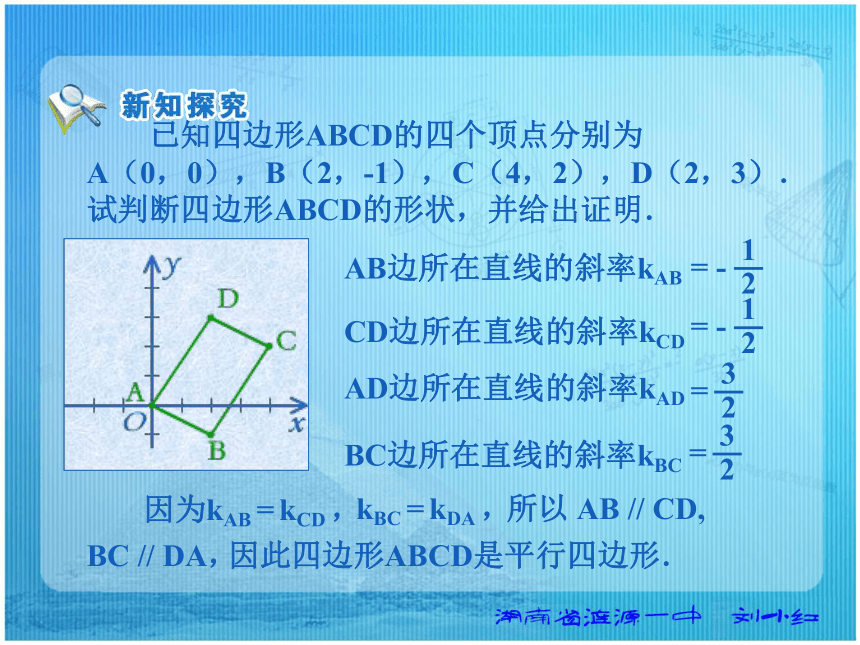
当两条直线互相平行且它们的斜率不存在时,这两条直线都垂直于x轴. 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.直线BA的斜率kBA直线PQ的斜率kPQ因为kBA = kPQ ,所以直线 BA // PQ 已知四边形ABCD的四个顶点分别为
A(0,0),B(2,-1),C(4,2),D(2,3).
试判断四边形ABCD的形状,并给出证明.AB边所在直线的斜率kAB因为kAB = kCD ,所以 AB // CD,CD边所在直线的斜率kCDAD边所在直线的斜率kADBC边所在直线的斜率kBCkBC = kDA ,BC // DA,因此四边形ABCD是平行四边形.思考:当l1⊥l2 时,k1与k2 满足什么关系?那么l1⊥ l2 ? k1k2 = -1若直线 l1⊥l 2 ,且有一条直线
的斜率不存在时,另一条直线的
斜率为0. 设直线 l1 ,l2 的斜率分别为k1 ,k2 已知A(-6,0),B(3,6),P(2,6),Q(4,3),试判断直线AB与直线PQ的位置关系.解:直线AB的斜率kAB 直线PQ的斜率kPQ 所以直线AB⊥PQ. 由于kABkPQ=-1 已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.解:AB边所在直线的斜率kAB
BC边所在直线的斜率kBC
有kAB kBC =-1,得AB⊥BC,
既∠ABC=90°.
所以△ABC是直角三角形.= 2判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2 平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5)解:(1)直线AB的斜率k2=2
因为l1 的斜率k1=2,
所以k1=k2
因此直线l1 // l2.判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2 平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5)解:(2)直线PQ的斜率k1=0
因为l2的斜率k2也为0且不经过P,Q两点,
所以直线l1//l2.判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5) 试确定m的值,使过点A(m,1),
B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行 (2)垂直 试确定m的值,使过点A(m,1),
B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行 (2)垂直
解: 已知过原点O的一条直线与函数y = log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数y = log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上;
(2)当BC平行于x轴时,求点A的坐标.
那么l1与l2的倾斜角相等
即α1=α2,
因此tanα1=tanα2
即k1= k2 对于两条不重合的直线l1,l2,它们的斜率分别为k1,k2,则有:l1// l2?k1= k2 对于同一平面内两条直线 l1,l2,
它们的斜率分别为 k1,k2,有
k1= k2 ? l1 // l2或 l1 与 l2 重合.
当两条直线互相平行且它们的斜率不存在时,这两条直线都垂直于x轴. 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.直线BA的斜率kBA直线PQ的斜率kPQ因为kBA = kPQ ,所以直线 BA // PQ 已知四边形ABCD的四个顶点分别为
A(0,0),B(2,-1),C(4,2),D(2,3).
试判断四边形ABCD的形状,并给出证明.AB边所在直线的斜率kAB因为kAB = kCD ,所以 AB // CD,CD边所在直线的斜率kCDAD边所在直线的斜率kADBC边所在直线的斜率kBCkBC = kDA ,BC // DA,因此四边形ABCD是平行四边形.思考:当l1⊥l2 时,k1与k2 满足什么关系?那么l1⊥ l2 ? k1k2 = -1若直线 l1⊥l 2 ,且有一条直线
的斜率不存在时,另一条直线的
斜率为0. 设直线 l1 ,l2 的斜率分别为k1 ,k2 已知A(-6,0),B(3,6),P(2,6),Q(4,3),试判断直线AB与直线PQ的位置关系.解:直线AB的斜率kAB 直线PQ的斜率kPQ 所以直线AB⊥PQ. 由于kABkPQ=-1 已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状.解:AB边所在直线的斜率kAB
BC边所在直线的斜率kBC
有kAB kBC =-1,得AB⊥BC,
既∠ABC=90°.
所以△ABC是直角三角形.= 2判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2 平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5)解:(1)直线AB的斜率k2=2
因为l1 的斜率k1=2,
所以k1=k2
因此直线l1 // l2.判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2 平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5)解:(2)直线PQ的斜率k1=0
因为l2的斜率k2也为0且不经过P,Q两点,
所以直线l1//l2.判断下列各小题中的不同直线l1,l2是否平行:
(1)l1的斜率为2,l2经过点A(1,2),B(4, 8)
(2) l1 经过点P(3,3),Q(-5,3), l2平行于x轴,但不经过P,Q两点
(3) l1经过点M(-1,0),N(-5,-2), l2 经过点R(-4,3),S(0,5) 试确定m的值,使过点A(m,1),
B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行 (2)垂直 试确定m的值,使过点A(m,1),
B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线
(1)平行 (2)垂直
解: 已知过原点O的一条直线与函数y = log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数y = log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上;
(2)当BC平行于x轴时,求点A的坐标.
