4.2.1直线与圆的位置关系

课件12张PPT。　　根据直线与圆的公共点的个数，平面几何中直线与圆的位置关系有几种？思考：对于直线方程Ax+By+c=0，圆的方程(x-a)2
+(y-b2)=r2，怎样利用方程来判断它们的位置关
系？ 已知直线3x+y-6=0和圆心为C的圆：x2+y2-2y-4=0，判断直线与圆的位置关系；如果相交，求出它们的交点坐标.思路一：利用圆心到直线的距
离与半径的长度进行比较.解：将圆的方程x2+y2-2y-4=0
写成标准形式： x2+(y-1)2=5圆心到直线的距离d= 所以直线与圆相交，有两个交点. 对于直线方程Ax+By+c=0，圆的方程(x-a)2+(y-b2)
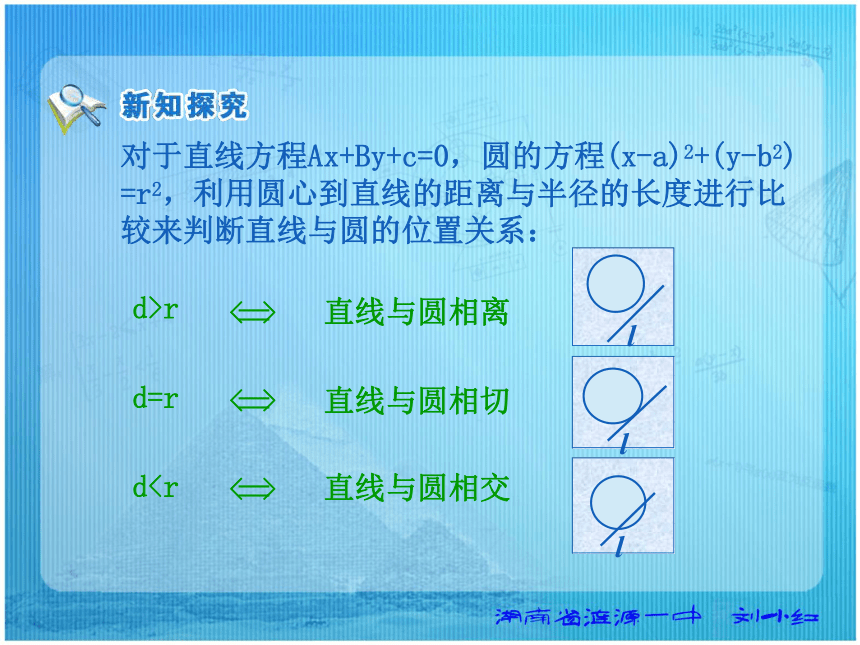
=r2，利用圆心到直线的距离与半径的长度进行比较来判断直线与圆的位置关系：d>r
d=r
d0得：x2-3x+2=0所以直线与圆相交，有两个公共点.解出：代入直线方程得y1=3，y2=0所以交点坐标为：（1，3），（2，0） x1=1，x2=2　　对于直线方程Ax+By+c=0，圆的方程(x-a)2
+(y-b2)=r2 ，利用方程组实数解的个数来判断直线与圆的位置关系：直线与圆相交直线与圆相切直线与圆相离设方程组解的个数为n△>0n=2△=0n=1△<0n=0解：将圆的方程写成标准形式得： x2+(y+2)2=25圆心坐标是(0,-2),半径r=5因为直线被圆所截得的弦长解：因为直线经过点(-3,-3)， 设直线方程为y+3=k(x+3)， 即kx-y+3k-3=0 所以所求直线方程分别为: 解出：即：x+2y+9=0或2x-y+3=0 所以直线3x+4y+2=0与圆x2+y2-2x
=0相切. 判断直线3x+4y+2=0与圆x2+y2-2x=0的位置关系.解：圆心坐标为（1，0），半径r=1.圆心到直线3x+4y+2=0的距离因为d=r， 　　已知直线：y=x+6，圆C：x2+y2-2y-4=0，试
判断直线l与圆C有无公共点，有几个公共点？解：整理得：x2+5x+10=0△=25-40 < 0 因此方程组无实数解，直线与圆相离.所以直线与圆没有公共点. 因此，圆心在原点，半径为7的圆C的方程为：　　已知直线4x+3y-35=0与圆心在原点的圆C相
切，求圆C的方程. 解： 原点O(0，0)到直线4x+3y-35=0的距离 所以圆的半径为7, x2+y2=49