4.2.2圆与圆的位置关系
图片预览





文档简介
课件13张PPT。圆与圆之间有几种位置关系? 根据圆O1:(x-a)2+(y-b)2=r12(r1>0),圆02:
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
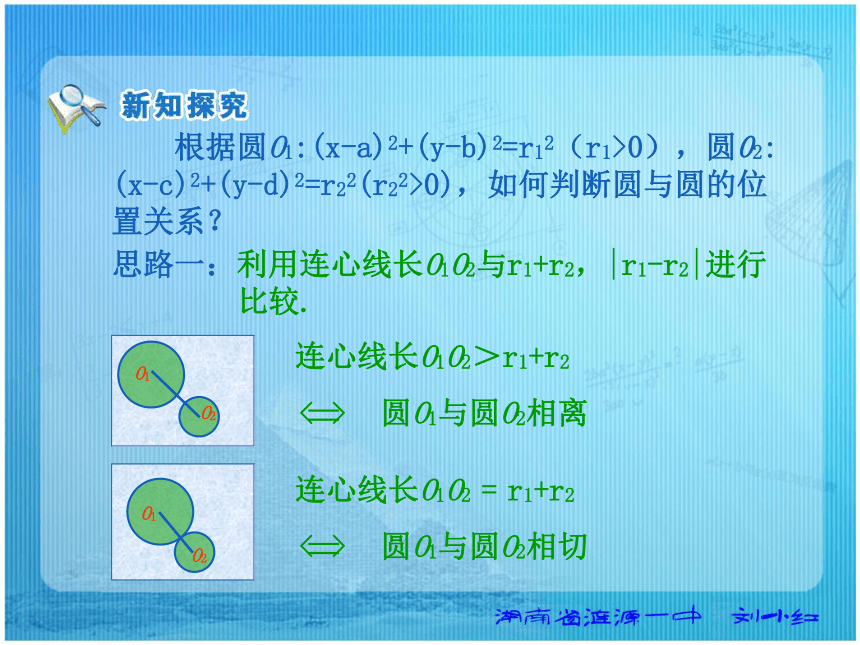
置关系? 思路一:利用连心线长O1O2与r1+r2,|r1-r2|进行
比较.连心线长O1O2>r1+r2 圆O1与圆O2相离 连心线长O1O2 = r1+r2 圆O1与圆O2相切 根据圆O1:(x-a)2+(y-b)2=r12(r1>0),圆02:
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
置关系? 连心线长O1O2=|r1-r2| 圆O1与圆O2内切 连心线长O1O2 < |r1-r2| 圆O1与圆O2内含 |r1-r2|<连心线长O1O2<r1+r2 圆O1与圆O2相交 根据圆O1:(x-a)2+(y-b)2=r12(r1>0),圆02:
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
置关系? 思路二:利用两个圆的方程组成的方程组实数解
的个数.圆O1与圆O2相交圆O1与圆O2相切圆O1与圆O2相离△>0n=2△=0n=1△<0n=0 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: 代入上式整理后得: x+2y-1=0 因为△=16 所以圆O1与圆O2相交,有两个公共点. x2-2x-3=0 >0 两个圆的相交弦所在的直线
方程. 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: x+2y-1=0 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:把圆与圆的方程写成标准方程,得:(x+1)2+(y+4)2=25. (x-2)2+(y-2)2=10. 圆C1的圆心是点(-1,-4),
半径长r1=5.圆C1:圆C2: 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.圆C1与圆C2连心线的长为:圆C1与圆C2的半径之和是:圆C1与圆C2的半径之差是:所以圆C1与圆C2相交,它们有两个交点. 已知圆C1:x2+y2+2x+3y+1=0,C2:x2+y2+4x+ 3y+2=0,判断圆C1与圆C2的位置关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: 代入圆C1整理后得: 因为△=144-16 所以圆C1与圆C2相交,有两个公共点. 4y2+12y+1=0 >0 求圆心在直线x-y-4=0,并且经过圆x2+y2+2x
+3y+1=0,C2:x2+y2+4x+3y+2=0的交点的圆的方程.解:设两个圆相交于A,B两点,得: 所以交点的坐标为: 因此直线AB的垂直平分线
的方程是:x+y+3=0 或A(-1,3),B(-6,-2) AB解方程组: 求圆心在直线x-y-4=0,并且经过圆x2+y2+2x
+3y+1=0,C2:x2+y2+4x+3y+2=0的交点的圆的方程.x+y+3=0与x-y-4=0联立,点C与点A的距离为:即x2+y2-x+7y-32=0. 所求的圆的方程为:|CA|= 已知地球和月球的半径分别为R、r,球心距
为d,求一宇宙飞船的轨道,使得在轨道上任一
点处看地球和月球的视角都相等.
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
置关系? 思路一:利用连心线长O1O2与r1+r2,|r1-r2|进行
比较.连心线长O1O2>r1+r2 圆O1与圆O2相离 连心线长O1O2 = r1+r2 圆O1与圆O2相切 根据圆O1:(x-a)2+(y-b)2=r12(r1>0),圆02:
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
置关系? 连心线长O1O2=|r1-r2| 圆O1与圆O2内切 连心线长O1O2 < |r1-r2| 圆O1与圆O2内含 |r1-r2|<连心线长O1O2<r1+r2 圆O1与圆O2相交 根据圆O1:(x-a)2+(y-b)2=r12(r1>0),圆02:
(x-c)2+(y-d)2=r22(r22>0),如何判断圆与圆的位
置关系? 思路二:利用两个圆的方程组成的方程组实数解
的个数.圆O1与圆O2相交圆O1与圆O2相切圆O1与圆O2相离△>0n=2△=0n=1△<0n=0 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: 代入上式整理后得: x+2y-1=0 因为△=16 所以圆O1与圆O2相交,有两个公共点. x2-2x-3=0 >0 两个圆的相交弦所在的直线
方程. 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: x+2y-1=0 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.解:把圆与圆的方程写成标准方程,得:(x+1)2+(y+4)2=25. (x-2)2+(y-2)2=10. 圆C1的圆心是点(-1,-4),
半径长r1=5.圆C1:圆C2: 已知圆C1:x2+y2+2x+8y-8=0,C2:x2+y2-4x- 4y-2=0,试判断圆C1与圆C2的关系.圆C1与圆C2连心线的长为:圆C1与圆C2的半径之和是:圆C1与圆C2的半径之差是:所以圆C1与圆C2相交,它们有两个交点. 已知圆C1:x2+y2+2x+3y+1=0,C2:x2+y2+4x+ 3y+2=0,判断圆C1与圆C2的位置关系.解:联立圆C1与圆C2的方程,得到方程组:①-②得: 代入圆C1整理后得: 因为△=144-16 所以圆C1与圆C2相交,有两个公共点. 4y2+12y+1=0 >0 求圆心在直线x-y-4=0,并且经过圆x2+y2+2x
+3y+1=0,C2:x2+y2+4x+3y+2=0的交点的圆的方程.解:设两个圆相交于A,B两点,得: 所以交点的坐标为: 因此直线AB的垂直平分线
的方程是:x+y+3=0 或A(-1,3),B(-6,-2) AB解方程组: 求圆心在直线x-y-4=0,并且经过圆x2+y2+2x
+3y+1=0,C2:x2+y2+4x+3y+2=0的交点的圆的方程.x+y+3=0与x-y-4=0联立,点C与点A的距离为:即x2+y2-x+7y-32=0. 所求的圆的方程为:|CA|= 已知地球和月球的半径分别为R、r,球心距
为d,求一宇宙飞船的轨道,使得在轨道上任一
点处看地球和月球的视角都相等.
