19.2.1 矩形
图片预览


文档简介
课件32张PPT。19.2 特殊的平行四边形
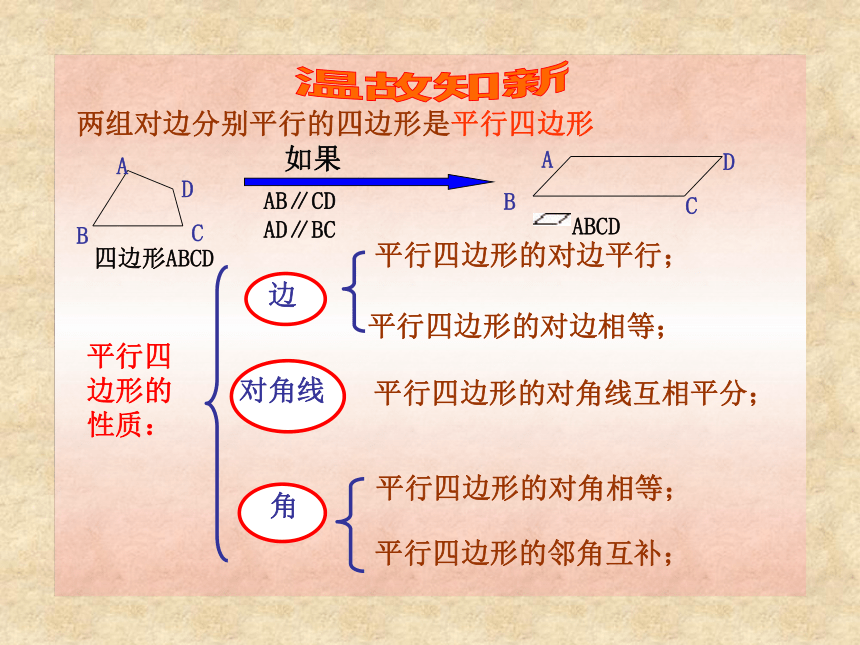
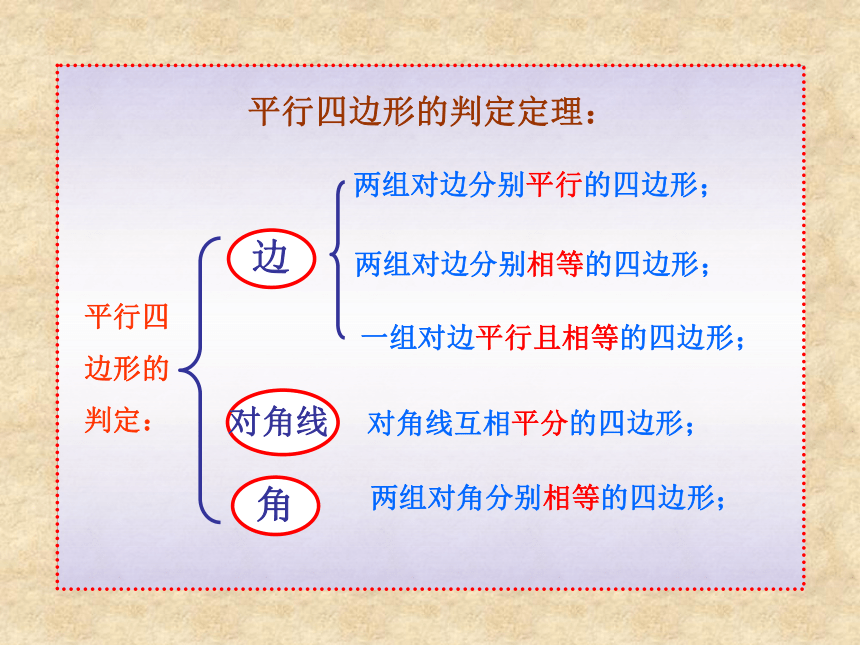
19.2.1 矩形两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理: 一个角是
直角两组对边
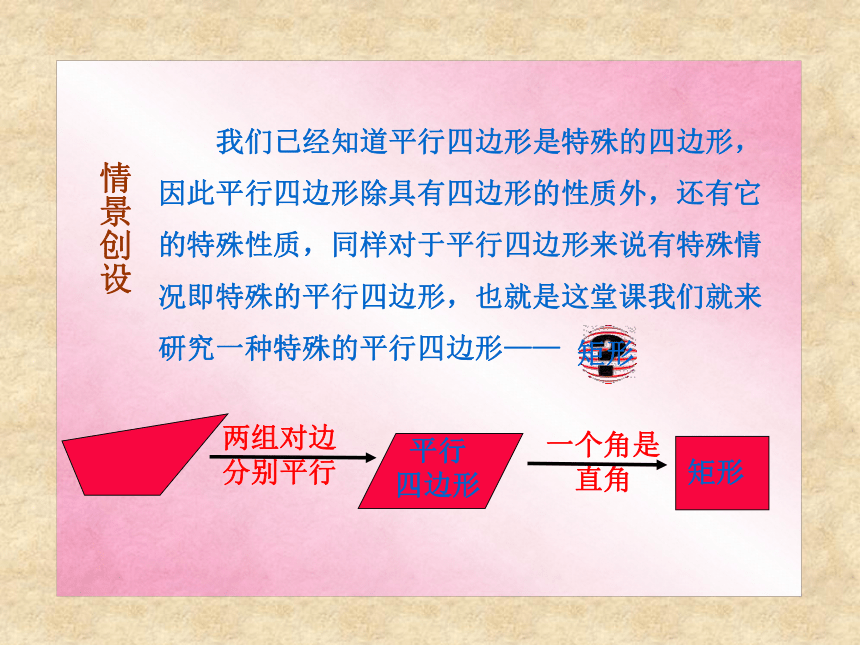
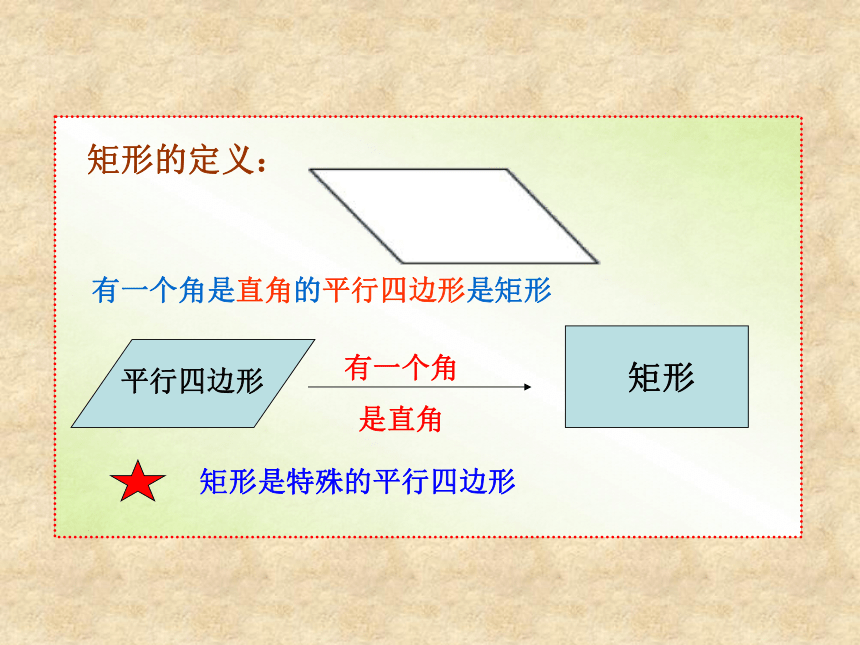
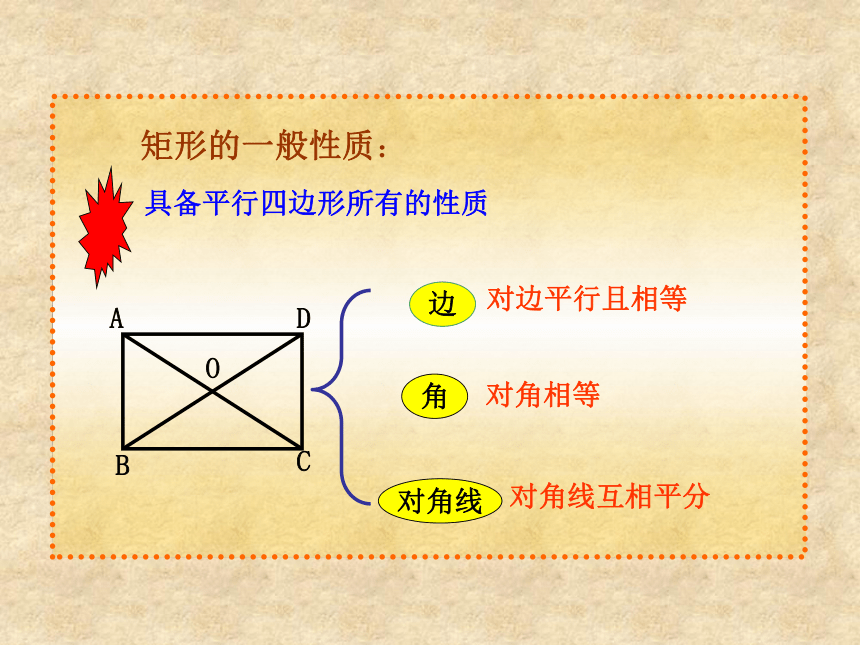
分别平行矩形情景创设 我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质: 探索新知:
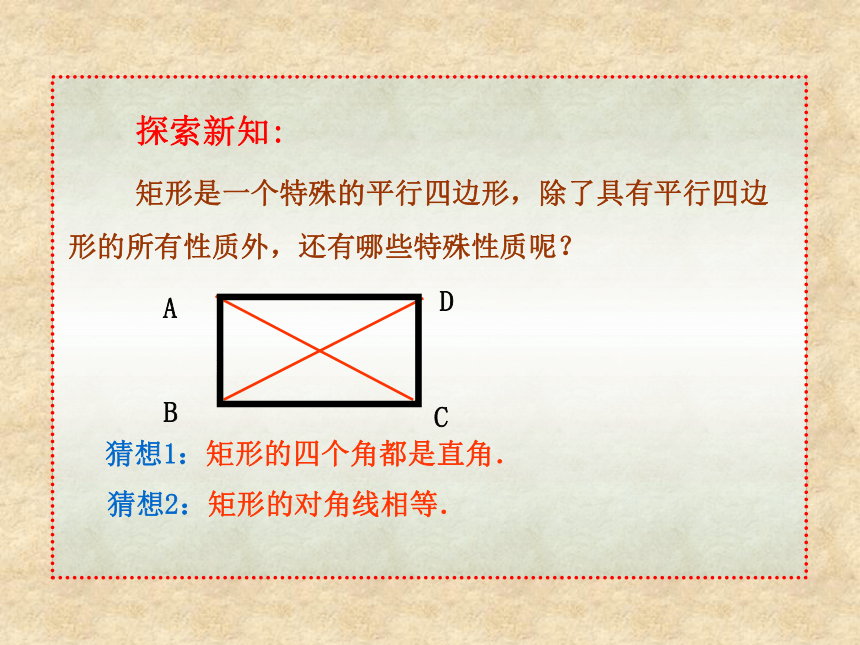
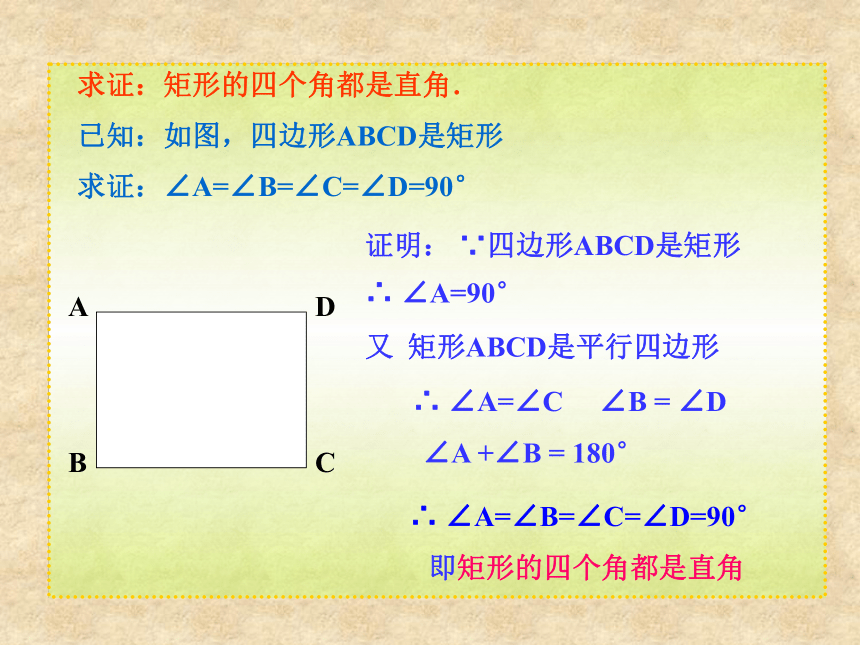
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
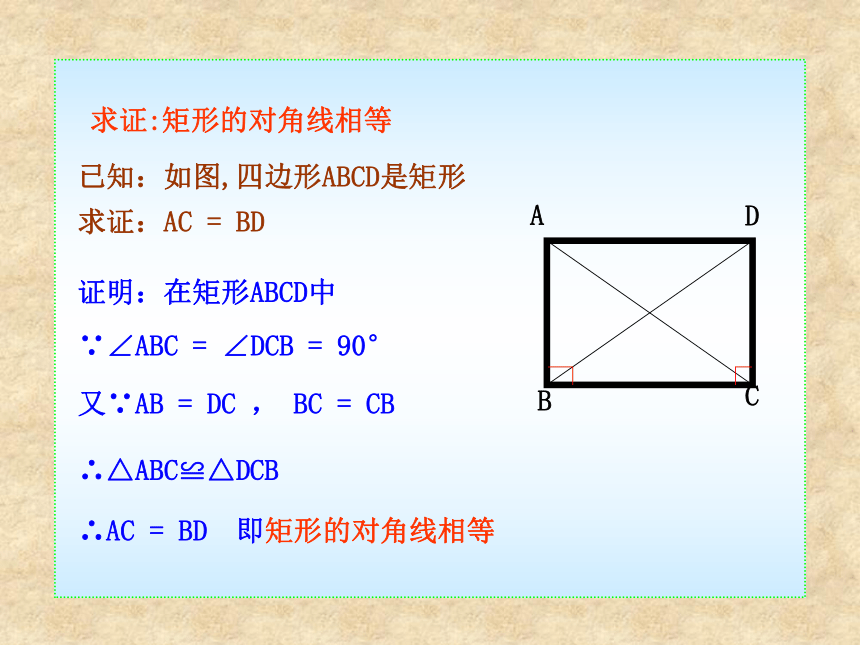
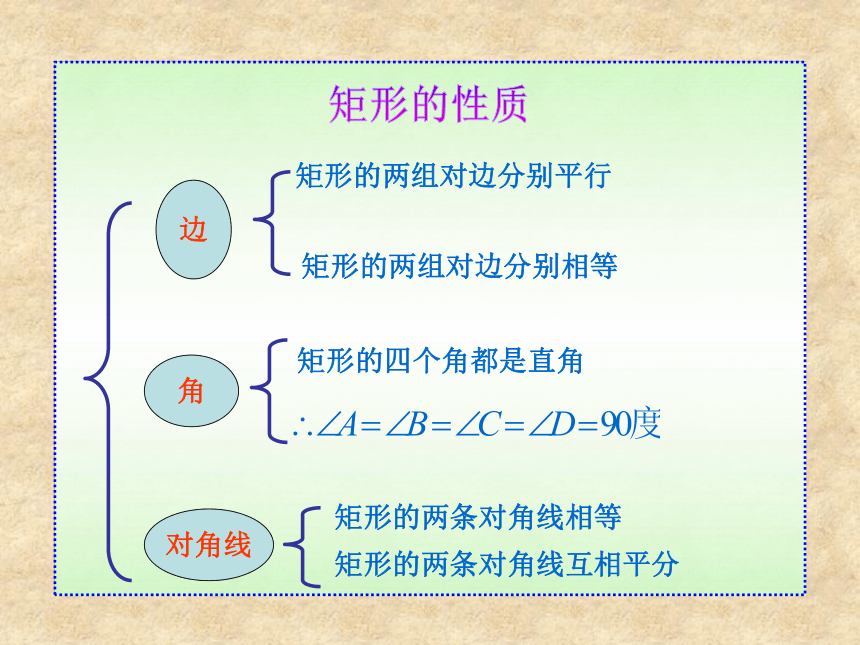
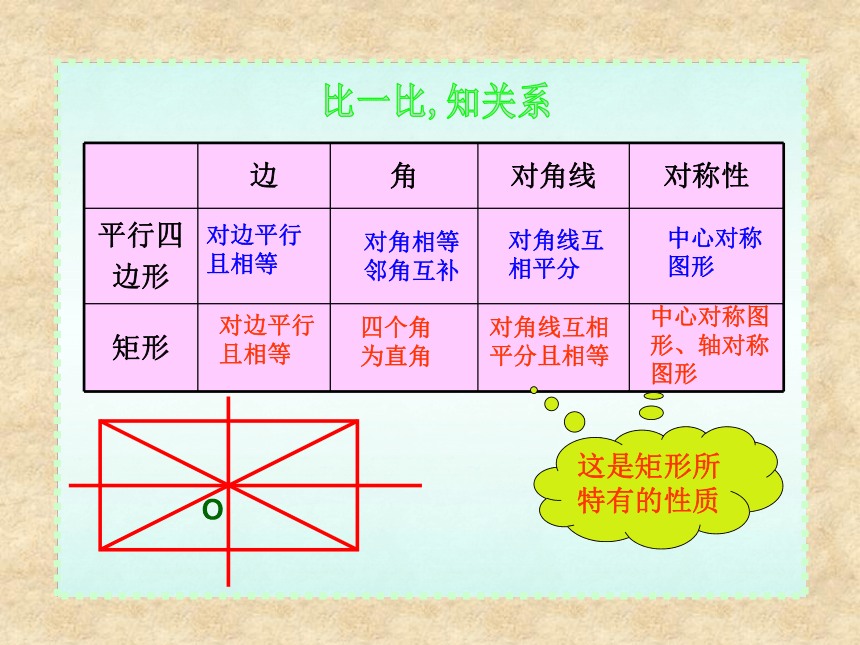
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形的两条对角线相等边对角线角矩形的性质比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形、轴对称图形O 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏已知:在Rt△ABC中,∠ABC=90 °,BO是AC上的中线.求证: BO = ACD证明: 延长BO至D,使OD=BO, 连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.∴AC=BD再探新知例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直2.过四边形的各个顶点分别作对角线的平行线,若这
四条平行线围成一个矩形,则原四边形一定是( )
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于( )
A.30° B.45° C.60° D.120° 你知道如何判定一个平行四边形是矩形吗?定义判定:有一个角是直角的平行四边形是矩形。(方法一)你还有其它的判定方法吗?ABCD∠A=90°四边形ABCD是矩形∵∴(已知)(矩形的定义)几何语言:情境二:李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边”这样,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?矩形的判定方法:有三个角是直角的四边形是矩形∵ ∠A=∠B=∠C=90°(已知)
∴四边形ABCD是矩形(有三个角是
直角的四边形是矩形)几何语言: 情境三:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形。命题:对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明 ∴ AB=CD, BC=BC(平行四边形对边相等)∴ △ABC≌ △DCB(SSS)∵四边形ABCD是平行四边(已知)在 △ABC和△DCB中AB=CD (已证)BC=BC (已证)AC=BD (已知)∴ ∠ABC=∠DCB(全等三角形对应边相等)又∵ ∠ABC+∠DCB=180°(平行四边形邻角互补) ∴ ∠ABC=90°(等式的性质)
又∵ 四边形ABCD是平行四边形(已知)∴四边形ABCD是矩形(矩形的定义)对角线相等的平行四边形是矩形矩形的判定方法:几何语言:∵ AC=BD,四边形ABCD是平行
四边形 (已知)∴四边形ABCD是矩形(对角线相等的平行四边形是矩形)你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。方法1:方法2:方法3:1、矩形具有而一般平行四边形不具有的性质是 ( ) 营中热身A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分2、下列四边形中不是矩形的是( )
A.有三个角是直角的四边形是矩形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形3、如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是
( )
A.一组对边平行而另一组对边不平行
B.对角线相等
C.对角线互相垂直
D.对角线相等互相平分已知:四边形ABCD是矩形
4.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
5.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝6.已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线(1)若BD=3㎝ 则AC= _______ ㎝
(2)若∠C=30°,AB=5㎝,则AC=_______㎝,BD=_______㎝.6510学习小结 互逆定理Thank you!
19.2.1 矩形两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理: 一个角是
直角两组对边
分别平行矩形情景创设 我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质: 探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形的两条对角线相等边对角线角矩形的性质比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形、轴对称图形O 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏已知:在Rt△ABC中,∠ABC=90 °,BO是AC上的中线.求证: BO = ACD证明: 延长BO至D,使OD=BO, 连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.∴AC=BD再探新知例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直2.过四边形的各个顶点分别作对角线的平行线,若这
四条平行线围成一个矩形,则原四边形一定是( )
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于( )
A.30° B.45° C.60° D.120° 你知道如何判定一个平行四边形是矩形吗?定义判定:有一个角是直角的平行四边形是矩形。(方法一)你还有其它的判定方法吗?ABCD∠A=90°四边形ABCD是矩形∵∴(已知)(矩形的定义)几何语言:情境二:李芳同学用四步画出了一个四边形,她的画法是“边——直角、边——直角、边——直角、边”这样,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?矩形的判定方法:有三个角是直角的四边形是矩形∵ ∠A=∠B=∠C=90°(已知)
∴四边形ABCD是矩形(有三个角是
直角的四边形是矩形)几何语言: 情境三:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形。命题:对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明 ∴ AB=CD, BC=BC(平行四边形对边相等)∴ △ABC≌ △DCB(SSS)∵四边形ABCD是平行四边(已知)在 △ABC和△DCB中AB=CD (已证)BC=BC (已证)AC=BD (已知)∴ ∠ABC=∠DCB(全等三角形对应边相等)又∵ ∠ABC+∠DCB=180°(平行四边形邻角互补) ∴ ∠ABC=90°(等式的性质)
又∵ 四边形ABCD是平行四边形(已知)∴四边形ABCD是矩形(矩形的定义)对角线相等的平行四边形是矩形矩形的判定方法:几何语言:∵ AC=BD,四边形ABCD是平行
四边形 (已知)∴四边形ABCD是矩形(对角线相等的平行四边形是矩形)你能归纳矩形的几种判定方法吗?有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。有三个角是直角的四边形是矩形。方法1:方法2:方法3:1、矩形具有而一般平行四边形不具有的性质是 ( ) 营中热身A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分2、下列四边形中不是矩形的是( )
A.有三个角是直角的四边形是矩形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形3、如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是
( )
A.一组对边平行而另一组对边不平行
B.对角线相等
C.对角线互相垂直
D.对角线相等互相平分已知:四边形ABCD是矩形
4.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
5.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝6.已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线(1)若BD=3㎝ 则AC= _______ ㎝
(2)若∠C=30°,AB=5㎝,则AC=_______㎝,BD=_______㎝.6510学习小结 互逆定理Thank you!
