七年级下学期镶嵌课件
图片预览








文档简介
课件32张PPT。罗平县长底民中
主讲:李岗好平整的地板!这是怎么铺成的?怎么一点空隙也没有?以上图形所涉及到的知识就是我们今天所要学的内容镶嵌(平面镶嵌) 同学们观察上面图形有什么特点?同学们再看看我们的教学楼墙上贴的墙砖,和我们脚下的地板砖有什么特点?
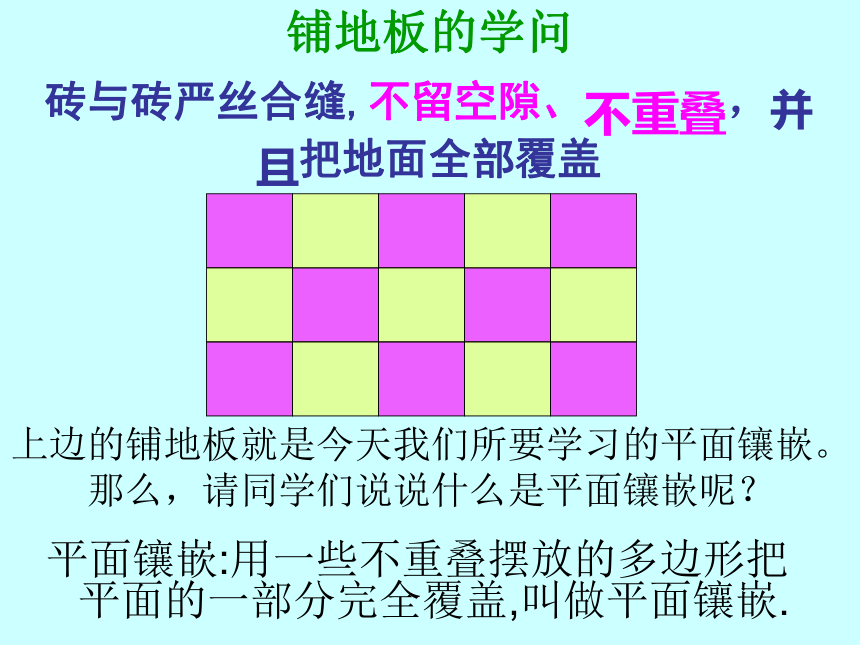
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖上边的铺地板就是今天我们所要学习的平面镶嵌。
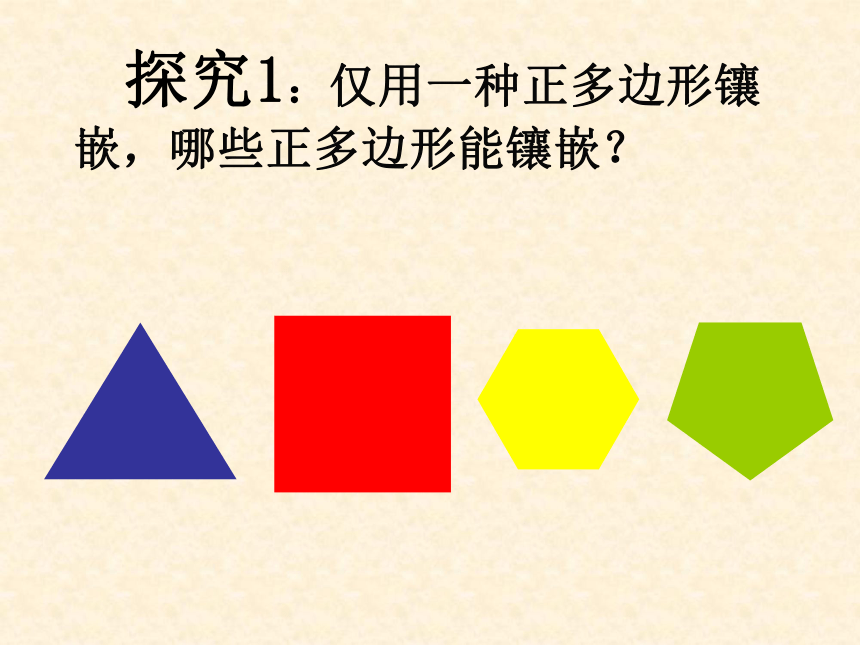
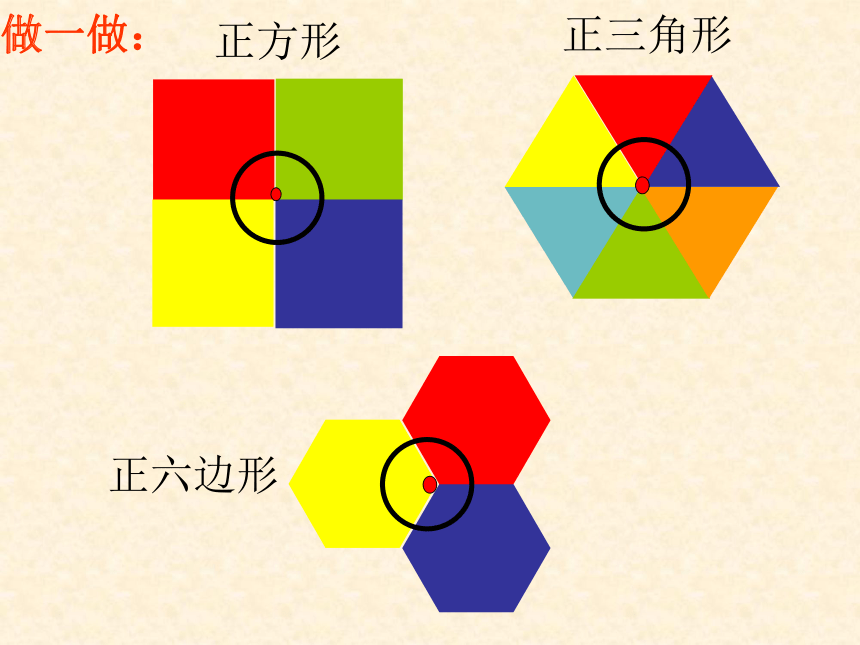
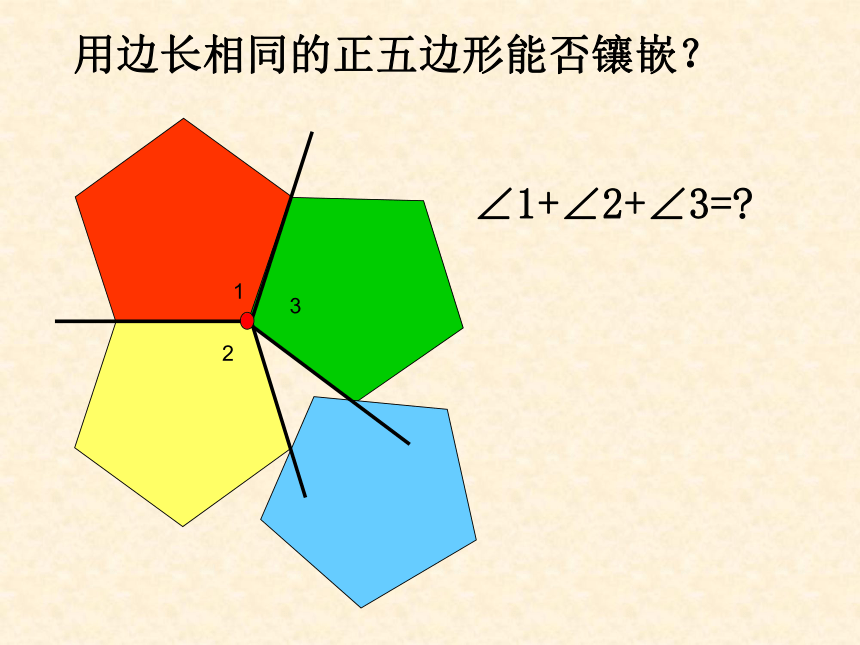
那么,请同学们说说什么是平面镶嵌呢? 探究1:仅用一种正多边形镶嵌,哪些正多边形能镶嵌?正方形正三角形正六边形做一做:123∠1+∠2+∠3=?用边长相同的正五边形能否镶嵌?铺满地面的多边形,围绕某
一点的内角和为( ) 360° 仅用一种正多边形能镶嵌的 关键是:这种正多边形的每个内角的度数能被360°整除。镶嵌满足的条件:
多边形的内角和为:(n-2) ●180°正多边形的每个内角为:下面,我们看看哪些图形能镶嵌,我们先复习一下以下知识180°360 °(5-2)●180 °
=540°(6-2)●180 °=720 °(7-2) ●180 °(8-2) ●180 °(9-2) ●180 °(10-2) ●180 °=900 °=1080 °=1440 °=1260 °60 °90 °540 °÷5=108 °720 °÷6=120 °900 °÷7≈128.6 °1080 °÷8=135 °140 °144 ° 仅用一种能进行镶嵌的正多边形只有正三角形(等边三角形),正四边形(正方形),正六边形,其它的正多边形都不能。60 °90 °120 °探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌?下面请同学们和我一起来讨论一下。60°×3+90°×2=360°讨 论正三角形和正方形正三角形和正六边形60°×4 + 120°=360°
60°×2+120°×2=360°135°135°90°150°150°60°正八边形和正方形正十二边形和正三角形正方形和正六边形几种正多边形能镶嵌的条件是:边长相等,且内角相加能凑成360°探究3:
用几个形状、大小相同的任意三角形能镶嵌吗?四边形呢?
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
∴任意三角形能镶嵌成平面图案。∵ ∠1+∠2+∠3+∠4=360°∴任意四边形能镶嵌成平面图案。
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗?为什么?多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°练习: 1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。3 2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正十八边形 D 小结:(1)镶嵌的含义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌(2)镶嵌成平面图案的条件是:多边形围绕某一点的内角和为360°
(3)任意一种三角形,任意一种四边形都能镶嵌。
(4)仅用一种能进行镶嵌的正多边形有:正三角形,正四边形,正六边形。(5)几种正多边形能镶嵌的条件是:边长相等,且内角相加能凑成360°镶嵌图片欣赏罗平红星广场正在兴建28层高楼,想用
两种正多边形的地砖来镶嵌地板,现正向
大家征集方案,小组合作设计几个吧?作业谢谢合作bye
主讲:李岗好平整的地板!这是怎么铺成的?怎么一点空隙也没有?以上图形所涉及到的知识就是我们今天所要学的内容镶嵌(平面镶嵌) 同学们观察上面图形有什么特点?同学们再看看我们的教学楼墙上贴的墙砖,和我们脚下的地板砖有什么特点?
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖上边的铺地板就是今天我们所要学习的平面镶嵌。
那么,请同学们说说什么是平面镶嵌呢? 探究1:仅用一种正多边形镶嵌,哪些正多边形能镶嵌?正方形正三角形正六边形做一做:123∠1+∠2+∠3=?用边长相同的正五边形能否镶嵌?铺满地面的多边形,围绕某
一点的内角和为( ) 360° 仅用一种正多边形能镶嵌的 关键是:这种正多边形的每个内角的度数能被360°整除。镶嵌满足的条件:
多边形的内角和为:(n-2) ●180°正多边形的每个内角为:下面,我们看看哪些图形能镶嵌,我们先复习一下以下知识180°360 °(5-2)●180 °
=540°(6-2)●180 °=720 °(7-2) ●180 °(8-2) ●180 °(9-2) ●180 °(10-2) ●180 °=900 °=1080 °=1440 °=1260 °60 °90 °540 °÷5=108 °720 °÷6=120 °900 °÷7≈128.6 °1080 °÷8=135 °140 °144 ° 仅用一种能进行镶嵌的正多边形只有正三角形(等边三角形),正四边形(正方形),正六边形,其它的正多边形都不能。60 °90 °120 °探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌?下面请同学们和我一起来讨论一下。60°×3+90°×2=360°讨 论正三角形和正方形正三角形和正六边形60°×4 + 120°=360°
60°×2+120°×2=360°135°135°90°150°150°60°正八边形和正方形正十二边形和正三角形正方形和正六边形几种正多边形能镶嵌的条件是:边长相等,且内角相加能凑成360°探究3:
用几个形状、大小相同的任意三角形能镶嵌吗?四边形呢?
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
∴任意三角形能镶嵌成平面图案。∵ ∠1+∠2+∠3+∠4=360°∴任意四边形能镶嵌成平面图案。
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗?为什么?多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°练习: 1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。3 2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正十八边形 D 小结:(1)镶嵌的含义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌(2)镶嵌成平面图案的条件是:多边形围绕某一点的内角和为360°
(3)任意一种三角形,任意一种四边形都能镶嵌。
(4)仅用一种能进行镶嵌的正多边形有:正三角形,正四边形,正六边形。(5)几种正多边形能镶嵌的条件是:边长相等,且内角相加能凑成360°镶嵌图片欣赏罗平红星广场正在兴建28层高楼,想用
两种正多边形的地砖来镶嵌地板,现正向
大家征集方案,小组合作设计几个吧?作业谢谢合作bye
