初一数学下学期第九章角复习学案

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
第九章 角
诸城市龙源学校 王志坚
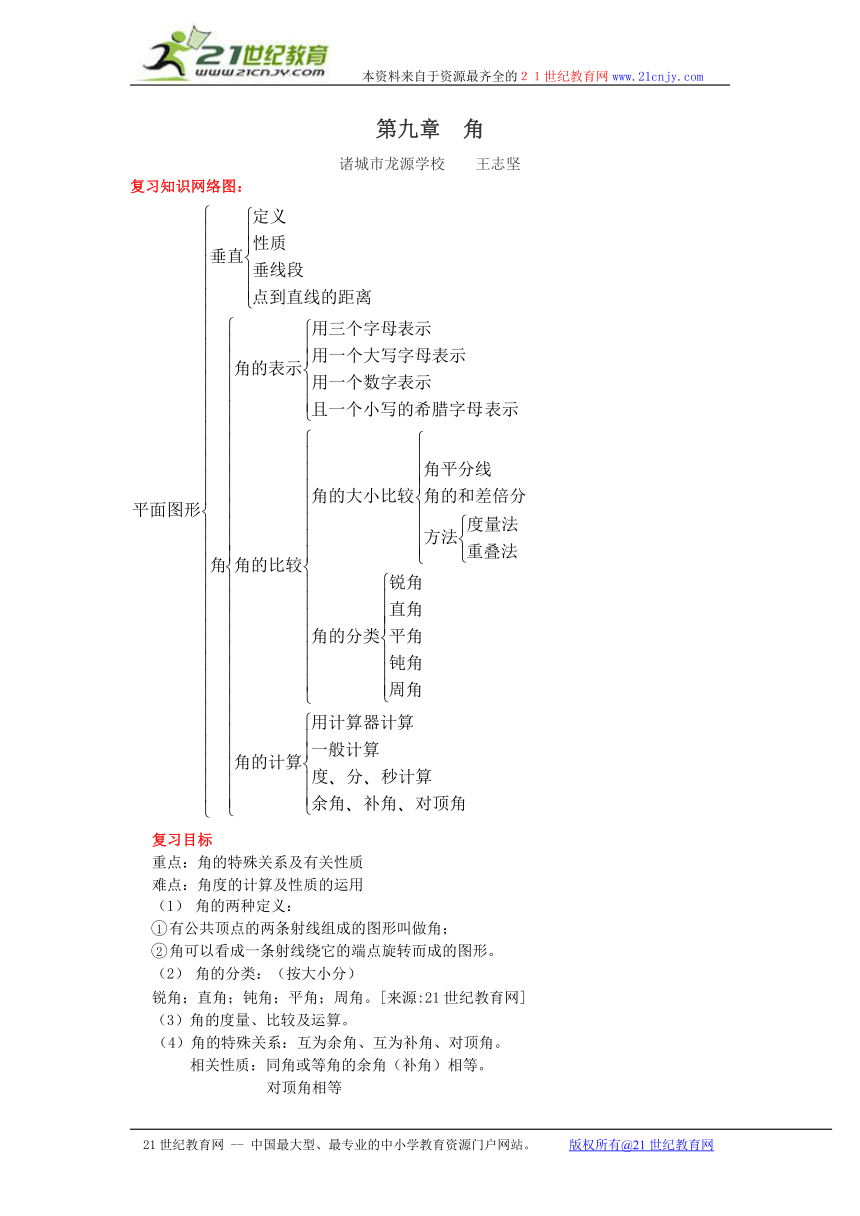
复习知识网络图：
复习目标
重点：角的特殊关系及有关性质
难点：角度的计算及性质的运用
（1） 角的两种定义：
1 有公共顶点的两条射线组成的图形叫做角；
2 角可以看成一条射线绕它的端点旋转而成的图形。
（2） 角的分类：（按大小分）
锐角；直角；钝角；平角；周角。[来源:21世纪教育网]
（3）角的度量、比较及运算。
（4）角的特殊关系：互为余角、互为补角、对顶角。
相关性质：同角或等角的余角（补角）相等。
对顶角相等
知识点回顾：
知识点一：角的定义及表示方法
1.角是由有 的两条射线所组成的图形。这两条射线叫做角的 ，它们的公共端点叫做角的 。
2. 角还可以看成是由 而成的图形。这是用运动的方式来定义。
3、角的表示方法有
同步测试：
1．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个的是（ ）
知识点二： 角平分线及角的大小比较
从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。如图：OC平分∠AOB，则（1）∠AOC=∠BOC= ∠AOB或（2） ∠AOC = ∠BOC =∠AOB。
同步测试：
1.已知∠AOB、∠AOC（∠AOB＞∠AOC )有一条公共边OA，OM是∠AOB的平分线，ON是∠AOC的平分线，则∠MON与∠BOC的大小有什么关系？请说明理由.
2．（2009年长沙）如图，于点是的平分线，则的度数为 ．答案：
知识点三：角的度量
1°=60′　 1′=60″ 　1直角=90° 1平角=180 ° 1周角=360°　
同步测试：
1．60°＝________平角，45°45′＝_____ _____度。
2．计算下列各题:
（1）23°30′＝____°;13．6°＝____°____′；
（2）52°45′－32°46′＝____°____′；
（3）18．3°+26°34′＝____°____′．
知识点四：对顶角
1. (2009年福建省泉州市)如右图，直线AB．CD相交于点O，∠1=50°，则∠2=　　　度
同步测试：
1. 如图，直线m和l交于O点，已知∠1的余角与它的补角的比为1：3，求∠2的度数。
知识点五：垂直
1. 经过一点可以画______条直线与已知直线垂直。
2、连接直线外一点与直线看各点的所有线段中， 最短。
同步测试：
1. 上午九点时分针与时针互相垂直，再经过 　　　分钟后分针与时针第一次成一条直线．
2. 一副三角板，如图所示叠放在一起，则图中∠α的度数是（ ）
(A) 75° (B)60°
(C) 65° (D)55°
例题讲解：
例1（1）用度、分、秒表示48.12°。
（2）用度表示50°7′30″。
解： ∵48.12°＝48°＋0.12°，0.12°＝60′×0.12＝7.2′＝7′＋0.2′，
0.2′＝60″×0.2＝12″，∴48.12°＝48°7′12″。
（2）∵50°7′30″＝50°＋7′＋30″＝50°＋7′＋0.5′＝50°＋7.5′
＝50°＋0.125°＝50.125°。
∴50°7′30″＝50.125°。
例2、 若一个角的余角与这个角的补角之比是2∶7，求这个角的邻补角．21世纪教育网
　　解题思路：这个问题涉及到一个角的余角、补角及两个角的比的概念，概念清楚了，问题不难解决．
　　解 设这个角为α，则这个角的余角为90°-α，这个角的补角为180°-α．依照题意，这两个角的比为
(90°-α)∶(180°-α)=2∶7．
　　所以
360°-2α=630°-7α，5α=270°，
　　所以α=54°．从而，这个角的邻补角为
180°-54°=126°．
例3 若时钟由2点30分走到2点50分，问时针、分针各转过多大的角度？
　　解题思路：解这个问题的难处在于时针转过多大的角度，这就要弄清楚时针与分针转动速度的关系．每一小时，分针转动360°，而时针转动
　　解 在2点30分时，时钟的分针指向数字6；在2点50分时，时钟的分针指向数字10，因此，分针共转过“四格”，每转“一格”为30°，故分针共转过了
4×30°=120°．
　　在钟表中，有很多有关分针、时针的转角问题．解决这类问题的关
　　倍)．
例4 已知如图，直线AB、CD相交于O，且 的度数是 的2倍.
求：（1） 、 的度数；
　　（2） 、 的度数.
解题思路：看图可知 与 是邻补角，从而有 ，而又知 ，于是可求出 与 的度数； 与 是对顶角， 与 是对顶角，由“对顶角相等”便可求 与 的度数.
　　解：（1）∵ AB是直线（已知）
∴ 与 是邻补角（邻补角定义）
∴ （补角定义）
设 的度数为x ，则 的度数为 ，
∴
即 ，
　　（2）∵ AB、CD相交于O（已知）
∴ ， （对顶角相等）
∵ ， （已求）
∴ ， （等量代换）
说明 已知两角的比值，通常设未知数，建立方程，通过解方程解决问题，是常驻考虑的一种思想方法.
随堂检测:
1．已知∠A=30°，则∠A的补角等于（ ）．
A．60° B．150° C．85° D．55°
2．如图1，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（ ）．
A．∠2=45° B．∠1=∠3
C．∠AOD与∠1互为补角 D．∠1的余角等于75°30′
(1) (2)
3．将矩形ABCD沿AE折叠，得如图2所示的图形，已知∠CED′=60°，则∠AED的大小是（ ）．
A．60° B．50° C．75° D．55°
4．如图3所示，在时刻8：30，时钟上的时针和分针之间的夹角为（ ）．
A．85° B．75° C．70° D．60°
5．如图4是圆规示意图，张开的两角所形成的角是（ ）．
A．平角 B．钝角 C．直角 D．锐角
(3) (4)
6．60°＝________平角，45°45′＝_____ _____度。
7.一个角的补角比它的余角大多少___________度。
8.若一个角的余角是这个角的4倍，则这个角的度数是
9.把63.5°用度分秒表示 ，把18°18′18″用度表示
10.如图，直线MN,PQ相交于O，OR平分∠MON,OK⊥PQ.　图中锐角有 　个，钝角有 个，∠ROK的余角是 ；∠ROK的补角是 .
11.计算（1）（36°15′24″＋13°21′54″）×3
（2）（180°－91°32′24″）÷2
同步练习
1．如果与互补，与互余，则与的关系是…………（ ）
（A）= （B） （C） （D）以上都不对
2.下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个的是（ ）
3．如图，∠1＝,∠AOC=点B、O、D在同一直线上，
则的度数为（ ）
（A） （B） （C） （D）
4、钟表在5点半时，它的时针与分针所成的锐角是（ ）
A．70° B．75° C．15° D．90°
5．（2009年福州）已知∠1=30°，则∠1的余角度数是（ ）
A．160° B．150° C．70° D．60°
6.下列叙述中正确的是（　　　）
(A)平角是一条直线　 (B)平角就是两个直角　
(C)两边成一条直线的角就是直角 (D)互补的角就是平角
7．如下图，在已知角内画射线，画1条射线，图中共有 个角；画2条射线，图中共有 个角；画3条射线，图中共有 个角，求画n条射线所得的角的个数 。
８、如图，将两块直角三角板的直角顶点重合为如图所示的形状，
若∠AOD＝127°，则∠BOC＝＿＿＿＿。
9. 如果一个角的余角与这个角的补角的和等于这个角的4倍，那么这个角等于_________．
10．（2009年湖南长沙）如图，于点是的平分线，则的度数为 ．
11.如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数.
12．如图，点A、O、E在同一直线上，∠AOB=40°，∠EOD=28°，OD平分∠COE， 求∠COB的度数.
13、如图所示，A，O，B在一条直线上，∠AOC=∠BOC+30°，OE平分∠BOC，求∠BOE21世纪教育网
A
E
D
B
C
A
O
D
B
C
第8题
A
E
D
B
C
A
O
E
B
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网