1.2.2.1函数的表示法
图片预览






文档简介
课件24张PPT。复习1、掌握求定义域的一般方法2、能求函数的函数值3、理解区间是表示数集的一种方法,
会把不等式转化为区间。针对性练习2.以下四组函数中,表示同一函数的是 ( )针对性练习3、针对性练习1.2.2 函数的表示法(第一课时)是函数 使对于集合A中的任意一个数 x ,
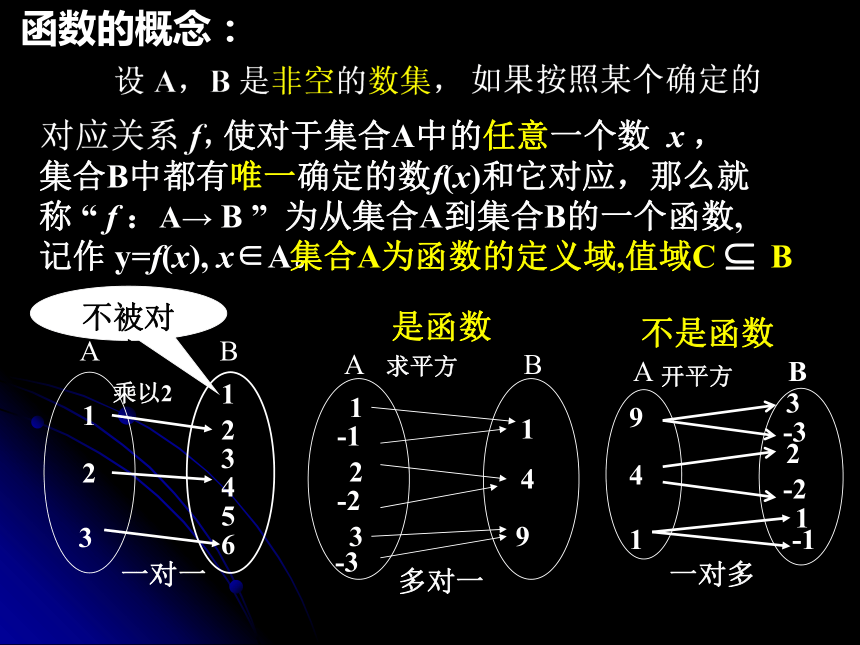
集合B中都有唯一确定的数f(x)和它对应,那么就
称 “ f :A→ B ” 为从集合A到集合B的一个函数,
记作 y=f(x), x∈A。 函数的概念:不是函数一对一多对一一对多不被对应集合A为函数的定义域,值域C B是函数1.2.2 函数的表示法(第一课时)列表法:
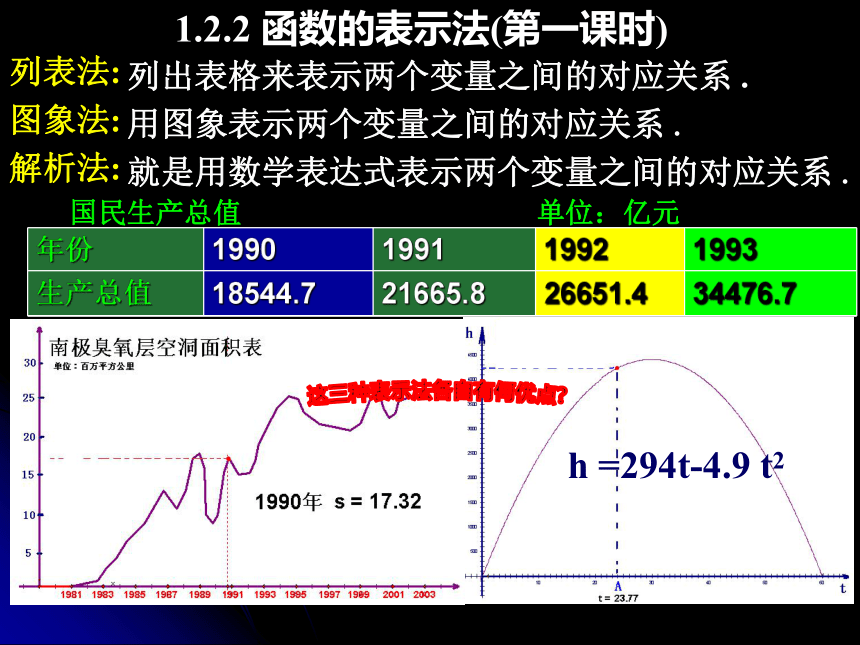
图象法:
解析法:国民生产总值 单位:亿元 这三种表示法各自有何优点?列出表格来表示两个变量之间的对应关系 .
用图象表示两个变量之间的对应关系 .
就是用数学表达式表示两个变量之间的对应关系 .h =294t-4.9 t21.2.2 函数的表示法(第一课时)列表法:
列出表格来表示两个变量的函数关系。
不需要计算就可以直接看出与自变量相应的函数值 .国民生产总值 单位:亿元 优点:图象法:
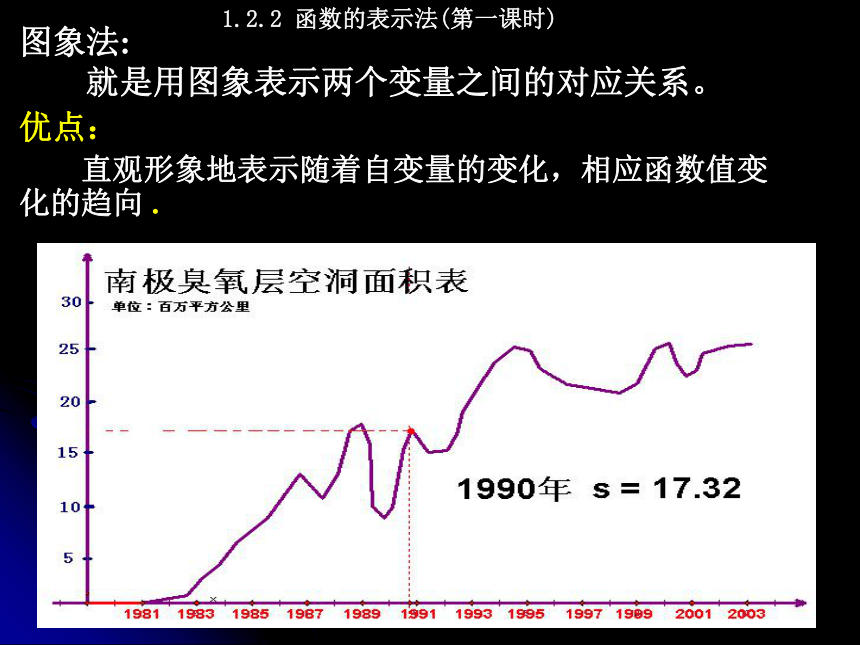
就是用图象表示两个变量之间的对应关系。
优点:
直观形象地表示随着自变量的变化,相应函数值变化的趋向 .1.2.2 函数的表示法(第一课时)解析法:就是用数学表达式表示两个 变量之间的对应关系.优点:
(1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值.如何运用函数的三种表示法表示函数? 例3. 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数y=f (x) .分析:你知道 “y=f (x)”的 含义吗?
它可以是解析表达式,可以是图象,也可以是对应值表.
解:这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f (x)表示为: y=5 x,
用列表法可将函数y=f (x)表示为:
用图象法可将函数y=f (x)表示为:思考:
若例3中的函数y=f(x)的定义域改为 [1,5],则其图象将会发生怎样的变化?x∈{1 , 2 , 3 , 4 , 5 }笔记本数 x钱数 y1 2 3 4 5 5 10 15 20 25 思考:
函数图象可以是连续的曲线,也可以是直线、折线、
离散的点等等;那么,如何判断在坐标平面中的图象是
否为函数图象呢?练习一.下列四个图像中,不是函数图像的是( ) 思考:
每一个函数都能用这三种方法表示吗? 2 这个函数能不能用解析法 ?
这个函数能不能用图象法 ?(1) 出生率与时间的函数关系. 如何选用恰当的函数表示法表示函数关系,
并进一步解决一些简单问题?例4.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:
请你对这三个同学在高一学年度的数学学习情况做一个分析. 解:从表中可知每位同学在每次测试中的成绩,
但不易分析每位同学的成绩变化情况 .
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将…..若将“成绩”与“测试序号”之间的关系用函数图象表示出来,
直观反映成绩变化:分析上图: 王伟同学的数学成绩始终高于班平均水平,
学习情况较为稳定且成绩优秀;
张成同学数学成绩不稳定,
总在班平均水平上下波动,且波动幅度较大;
赵磊同学数学成绩低于班级平均水平,
但他的成绩呈上升趋势,表明他的成绩在稳步提高.
思考 :
本题可否用列表法表示函数,如果可以,应怎样列表? 例6.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程
为20公里,请根据题意,写出票价
与里程之间的函数解析式,并画出
函数图象。 解:设票价为y,里程为x,
则x∈(0,20], 所以依题意可得:动感演示分段函数:
就是函数在它的定义域中,
对于自变量x的不同取值范围,
对应关系不同.思考:
分段函数的解析式有何特点,如何正确书写?练习二:课本P23
1. 如图,把截面半径为25 cm 的圆形
木头锯成矩形木料,如果矩形的一边长为x,
面积为 y ,把y表示为x的函数 .必须注明
函数的定义域范围. 2.下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写一件事.
(1) 我离家不久, 发现自己把作业本放在家里了,于是返回家找到作业本再上学;
(2) 我骑着车一路匀速行驶, 只是再途中遇到一次交通堵塞, 耽搁了一些时间;
(3) 我出发后, 心情轻松, 缓缓行进, 后来为了赶时间开始加速.(C):我一开始看错时间,越走越快,后来想起自己的表比北京时间快十分钟,才放慢脚步.ABD例5. 画出函数y = | x |的图象,
并判断该函数是不是分段函数。解:由绝对值的概念 可得:
建直角坐标系,取点 ,描点,
连线可得
函数y = | x |的图象
(如左上侧)。
该函数是不是分段函数?小结思考题: 画出下列函数的图象: 比较上面两个函数的图象,思考函数y=f(x)和y=|f(x)|
图象的关系? 小 结:
一、明确函数的三种表示方法及各自的优点;
列表法的优点:不需要计算就可以直接看出与自变量相应的函 数值.
图象法的优点:能直观形象地表示出函数的变化情况 .
解析法的优点:
(1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值 .
二、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
三、注意分段函数的表示方法及其图象的画法, 并能简单应用.
四、以后解决函数问题时, 还要注意三种方法的有机结合.作业:
P24 习题1.2 A组 第7、9题
预习: 课本P22~23,思考下面两个问题:
1.什么是映射?
2.函数和映射有什么联系?思考题
会把不等式转化为区间。针对性练习2.以下四组函数中,表示同一函数的是 ( )针对性练习3、针对性练习1.2.2 函数的表示法(第一课时)是函数 使对于集合A中的任意一个数 x ,
集合B中都有唯一确定的数f(x)和它对应,那么就
称 “ f :A→ B ” 为从集合A到集合B的一个函数,
记作 y=f(x), x∈A。 函数的概念:不是函数一对一多对一一对多不被对应集合A为函数的定义域,值域C B是函数1.2.2 函数的表示法(第一课时)列表法:
图象法:
解析法:国民生产总值 单位:亿元 这三种表示法各自有何优点?列出表格来表示两个变量之间的对应关系 .
用图象表示两个变量之间的对应关系 .
就是用数学表达式表示两个变量之间的对应关系 .h =294t-4.9 t21.2.2 函数的表示法(第一课时)列表法:
列出表格来表示两个变量的函数关系。
不需要计算就可以直接看出与自变量相应的函数值 .国民生产总值 单位:亿元 优点:图象法:
就是用图象表示两个变量之间的对应关系。
优点:
直观形象地表示随着自变量的变化,相应函数值变化的趋向 .1.2.2 函数的表示法(第一课时)解析法:就是用数学表达式表示两个 变量之间的对应关系.优点:
(1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值.如何运用函数的三种表示法表示函数? 例3. 某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数y=f (x) .分析:你知道 “y=f (x)”的 含义吗?
它可以是解析表达式,可以是图象,也可以是对应值表.
解:这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f (x)表示为: y=5 x,
用列表法可将函数y=f (x)表示为:
用图象法可将函数y=f (x)表示为:思考:
若例3中的函数y=f(x)的定义域改为 [1,5],则其图象将会发生怎样的变化?x∈{1 , 2 , 3 , 4 , 5 }笔记本数 x钱数 y1 2 3 4 5 5 10 15 20 25 思考:
函数图象可以是连续的曲线,也可以是直线、折线、
离散的点等等;那么,如何判断在坐标平面中的图象是
否为函数图象呢?练习一.下列四个图像中,不是函数图像的是( ) 思考:
每一个函数都能用这三种方法表示吗? 2 这个函数能不能用解析法 ?
这个函数能不能用图象法 ?(1) 出生率与时间的函数关系. 如何选用恰当的函数表示法表示函数关系,
并进一步解决一些简单问题?例4.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:
请你对这三个同学在高一学年度的数学学习情况做一个分析. 解:从表中可知每位同学在每次测试中的成绩,
但不易分析每位同学的成绩变化情况 .
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将…..若将“成绩”与“测试序号”之间的关系用函数图象表示出来,
直观反映成绩变化:分析上图: 王伟同学的数学成绩始终高于班平均水平,
学习情况较为稳定且成绩优秀;
张成同学数学成绩不稳定,
总在班平均水平上下波动,且波动幅度较大;
赵磊同学数学成绩低于班级平均水平,
但他的成绩呈上升趋势,表明他的成绩在稳步提高.
思考 :
本题可否用列表法表示函数,如果可以,应怎样列表? 例6.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程
为20公里,请根据题意,写出票价
与里程之间的函数解析式,并画出
函数图象。 解:设票价为y,里程为x,
则x∈(0,20], 所以依题意可得:动感演示分段函数:
就是函数在它的定义域中,
对于自变量x的不同取值范围,
对应关系不同.思考:
分段函数的解析式有何特点,如何正确书写?练习二:课本P23
1. 如图,把截面半径为25 cm 的圆形
木头锯成矩形木料,如果矩形的一边长为x,
面积为 y ,把y表示为x的函数 .必须注明
函数的定义域范围. 2.下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写一件事.
(1) 我离家不久, 发现自己把作业本放在家里了,于是返回家找到作业本再上学;
(2) 我骑着车一路匀速行驶, 只是再途中遇到一次交通堵塞, 耽搁了一些时间;
(3) 我出发后, 心情轻松, 缓缓行进, 后来为了赶时间开始加速.(C):我一开始看错时间,越走越快,后来想起自己的表比北京时间快十分钟,才放慢脚步.ABD例5. 画出函数y = | x |的图象,
并判断该函数是不是分段函数。解:由绝对值的概念 可得:
建直角坐标系,取点 ,描点,
连线可得
函数y = | x |的图象
(如左上侧)。
该函数是不是分段函数?小结思考题: 画出下列函数的图象: 比较上面两个函数的图象,思考函数y=f(x)和y=|f(x)|
图象的关系? 小 结:
一、明确函数的三种表示方法及各自的优点;
列表法的优点:不需要计算就可以直接看出与自变量相应的函 数值.
图象法的优点:能直观形象地表示出函数的变化情况 .
解析法的优点:
(1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值 .
二、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
三、注意分段函数的表示方法及其图象的画法, 并能简单应用.
四、以后解决函数问题时, 还要注意三种方法的有机结合.作业:
P24 习题1.2 A组 第7、9题
预习: 课本P22~23,思考下面两个问题:
1.什么是映射?
2.函数和映射有什么联系?思考题
