1.1 程序框图与算法的基本结构
文档属性
| 名称 | 1.1 程序框图与算法的基本结构 |

|
|
| 格式 | rar | ||
| 文件大小 | 908.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-13 00:00:00 | ||
图片预览

文档简介
课件25张PPT。1.1.2 程序框图与算法的基本
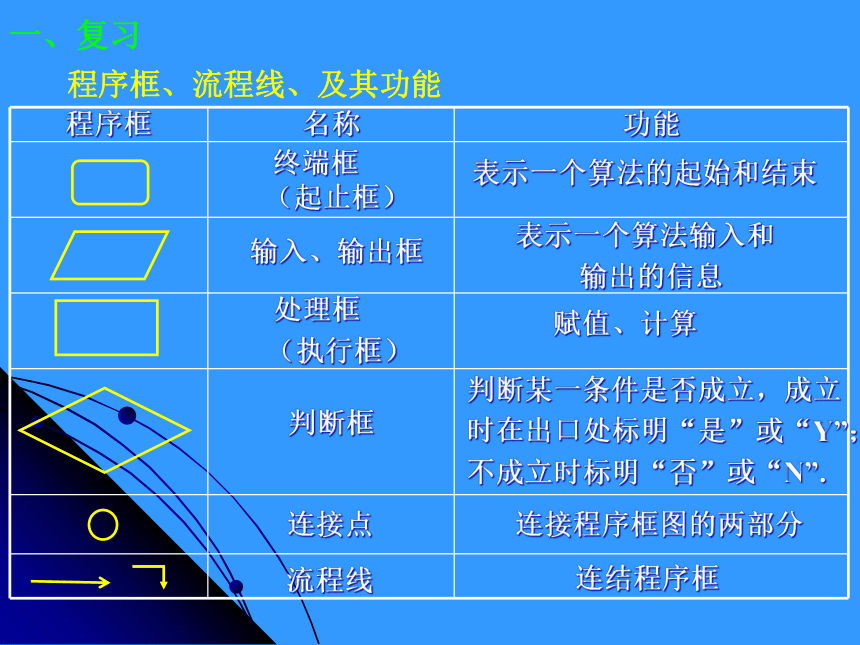
逻辑结构(二)09-05-20 终端框
(起止框)表示一个算法的起始和结束输入、输出框表示一个算法输入和
输出的信息 处理框
(执行框)赋值、计算判断框判断某一条件是否成立,成立
时在出口处标明“是”或“Y”;
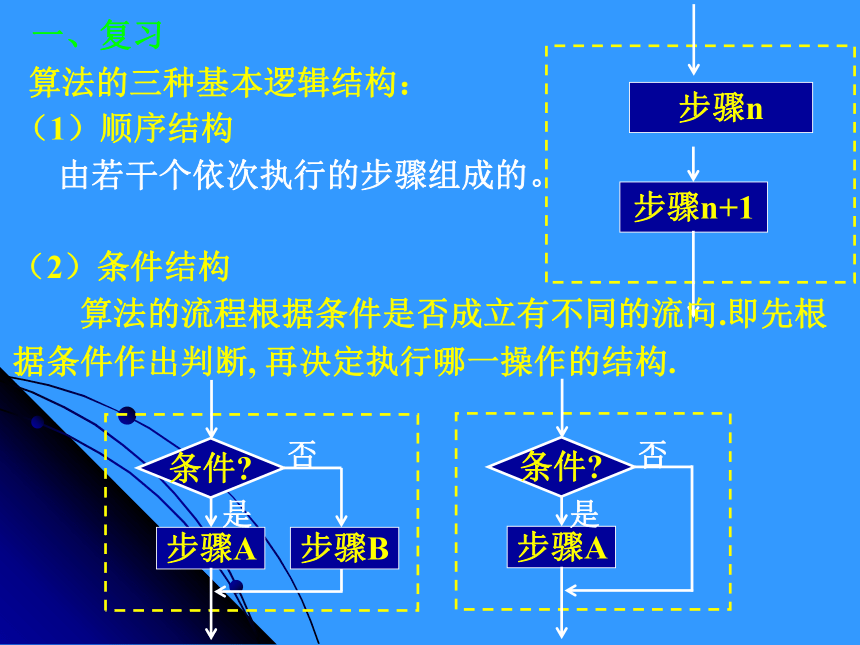
不成立时标明“否”或“N”.连接点连接程序框图的两部分流程线连结程序框程序框、流程线、及其功能一、复习算法的三种基本逻辑结构:一、复习(1)顺序结构
由若干个依次执行的步骤组成的。(2)条件结构
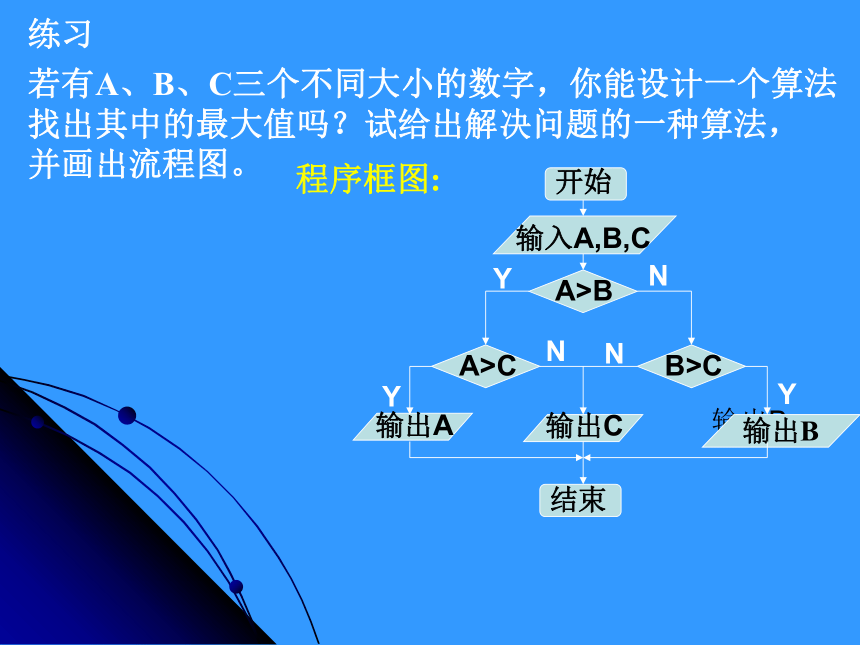
算法的流程根据条件是否成立有不同的流向.即先根据条件作出判断, 再决定执行哪一操作的结构.若有A、B、C三个不同大小的数字,你能设计一个算法
找出其中的最大值吗?试给出解决问题的一种算法,
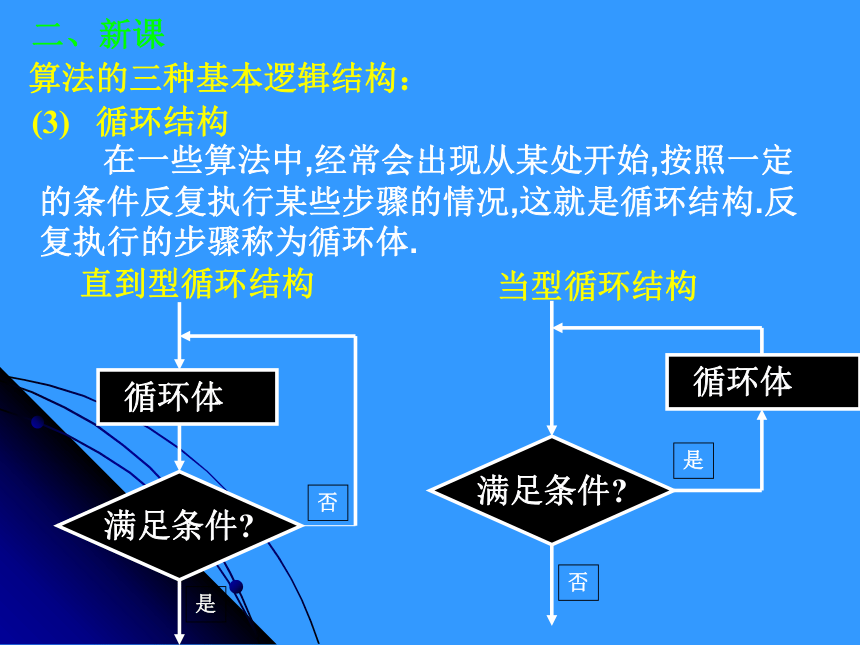
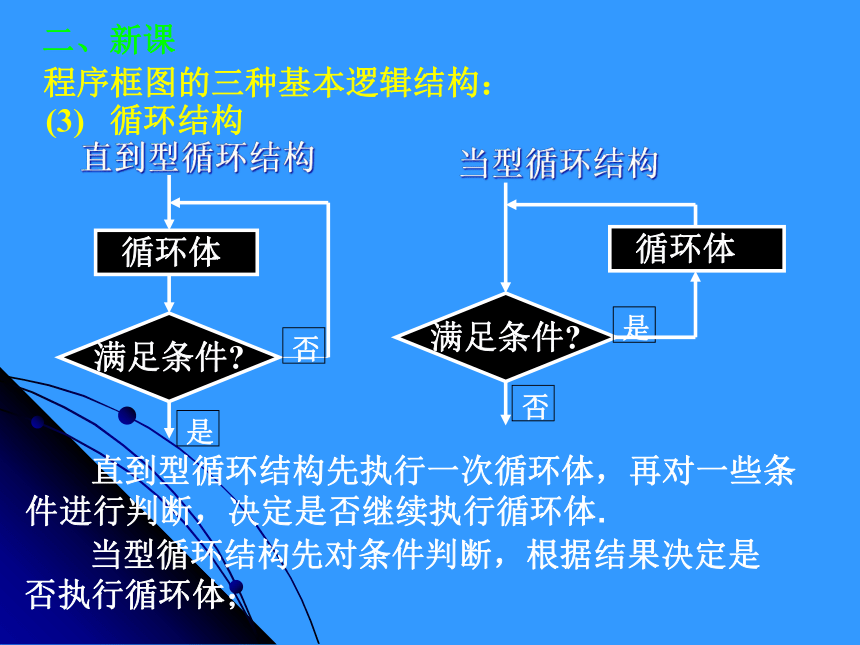
并画出流程图。练习程序框图:作业评讲 P20 3程序框图:算法:(3) 循环结构 在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.直到型循环结构 循环体满足条件?是否当型循环结构满足条件?否是 循环体二、新课算法的三种基本逻辑结构:
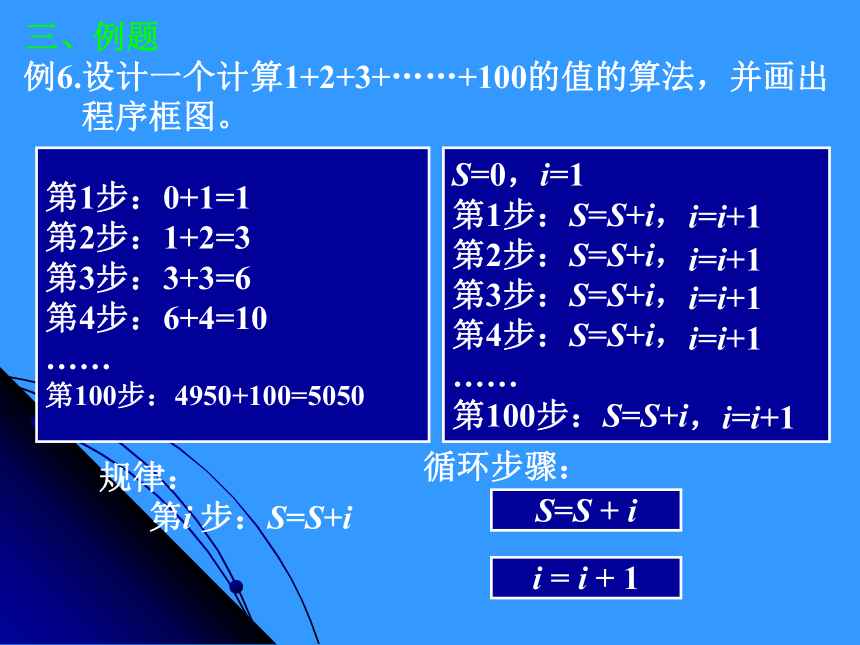
当型循环结构先对条件判断,根据结果决定是否执行循环体; 直到型循环结构先执行一次循环体,再对一些条件进行判断,决定是否继续执行循环体.(3) 循环结构二、新课程序框图的三种基本逻辑结构:第1步:0+1=1
第2步:1+2=3
第3步:3+3=6
第4步:6+4=10
……
第100步:4950+100=5050规律:
第i 步:S=S+iS=0,i=1
第1步:S=S+i,
第2步:S=S+i,
第3步:S=S+i,
第4步:S=S+i,
……
第100步:S=S+ii=i+1i=i+1i=i+1i=i+1S=S + ii = i + 1,i=i+1例6.设计一个计算1+2+3+……+100的值的算法,并画出
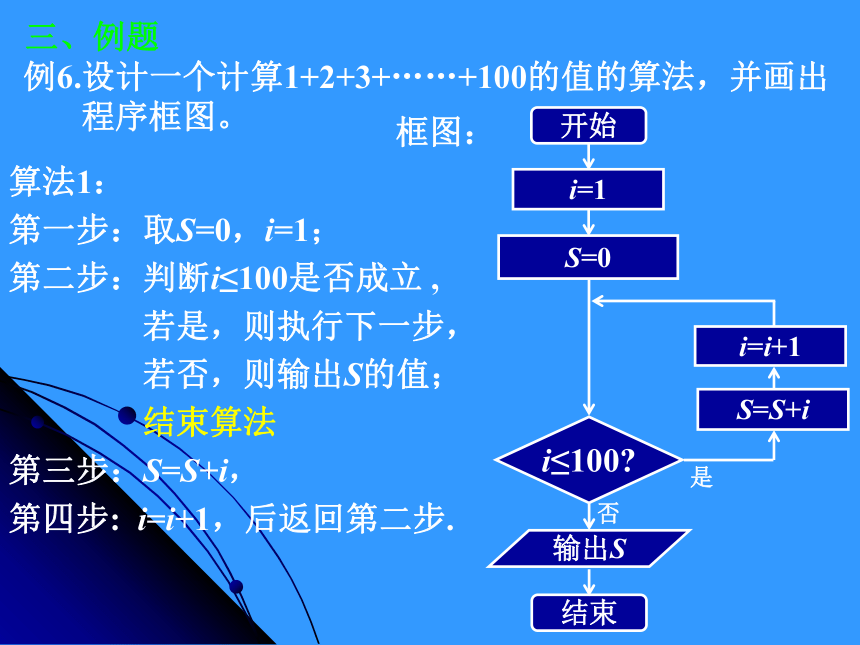
程序框图。循环步骤:三、例题开始S=0输出S结束i=1i≤100?S=S+ii=i+1框图:算法1:
第一步:取S=0,i=1;
第二步:判断i≤100是否成立 ,
若是,则执行下一步,
若否,则输出S的值;
结束算法
第三步:S=S+i,
第四步: i=i+1,后返回第二步.例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题框图:开始S=0输出S结束i=1i>100?S=S+ii=i+1算法2:
第一步:取S=0,i=1;
第二步:计算S=S+i,i=i+1;
第三步:判断i>100是否成立 ,
若否,则返回第二步,
若是,则输出S的值;例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题当型循环结构直到型循环结构S:累加变量
i:计数变量例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题变式1:设计一个计算1+2+3+……+100的值的算法,
并画出程序框图。变式2:设计一个计算1+2+3+……+100的值的算法,
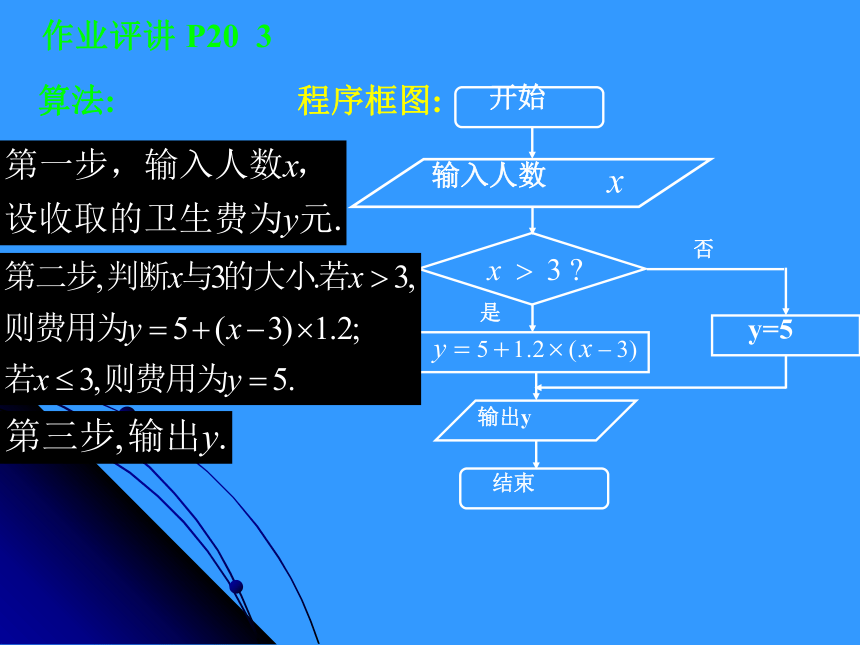
并画出程序框图。例7.某工厂2005年的年生产总值为200万元,技术革新后预计以后
每年的年生产总值都比上一年增长5﹪.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.算法:第一步,输入2005年的年生产总值.第二步,计算下一年的年生产总值.第三步,判断所得的结果是否大于
300.若是,则输出该年的年份;否则
返回第二步. 程序框图: a > 300 ?否三、例题 程序框图: a > 300 ?否请将该循环结构改为当型循环例3:写出用“二分法”求方程x2-2=0(x>0)的近似
解的算法第一步:令f(x)=x2-2,给定精确度d第二步:确定区间[a,b],满足f(a)f(b)<0第四步:若f(a)f(m)<0,则含零点的区间为[a,m],否则
含零点的区间为[m,b],将新得到的含零点的
区间仍记为[a,b]第五步:判断[a,b]的长度是否小于d或f(m)是否等于
零,若是,则m是方程的近似解,否则返
回第三步四、程序框图的画法(1).算法步骤中的“第一步”,
“第二步”, “第三步”可以用顺序结构来表示。(2).算法步骤中的
“第四步”,可以
用条件结构来表示。是否 (3).算法步骤中的“第五步”包含一个条件结构,这个条件结构与“第三步”, “第四步”构成一个循环结构。第三步第四步输出m是否 (4).将各步骤的程序框图连接起来,并画出“开始”和
“结束”两个终端框,就得到了表示整个算法的程序框图.设计一个算法的程序框图的步骤:第一步,用自然语言表述算法步骤. 第二步,确定每一个算法步骤所包含的逻辑结构,并用相应的程序框图表示,得到该步骤的程序框图. 第三步,将所有步骤的程序框图用流程线连接起来,并加上终端框,得到表示整个算法的程序框图.是否输出m开始结束是否①①②②的值,并画出程序框图.开始输入一个正整数n输入S的值结束S=0i=1S=S+1/ii=i+1i>n?NY设计一个算法求 思考:将步骤A和步骤B交换位置,结果会怎样?能达到预期结果吗?为什么?要达到预期结果,还需要做怎样的修改?练习: 对任意正整数n,小结1、循环结构的特点2、循环结构的框图表示3、循环结构有注意的问题避免死循环的出现,设置好进入(结束)循环体的条件。当型和直到型重复同一个处理过程习题1.1 A组 第2题
作业1.若已知梯形的上底为a,下底为b,高为h,试设计一个
求该梯形面积的算法,并画出程序框图。
2.设计一个求任意数的绝对值的算法,并画出程序框图。1. 算法:第一步:输入a,b,h的值;第三步:输出梯形的面积S。框图:开始输出S结束输入a,b,h练习2. 算法:第一步:输入x的值;第二步:若x≥0,则输出x;
若否,则输出-x;框图:开始输入xx≥0?输出-x输出x结束1.若已知梯形的上底为a,下底为b,高为h,试设计一个
求该梯形面积的算法,并画出程序框图。
2.设计一个求任意数的绝对值的算法,并画出程序框图。练习
逻辑结构(二)09-05-20 终端框
(起止框)表示一个算法的起始和结束输入、输出框表示一个算法输入和
输出的信息 处理框
(执行框)赋值、计算判断框判断某一条件是否成立,成立
时在出口处标明“是”或“Y”;
不成立时标明“否”或“N”.连接点连接程序框图的两部分流程线连结程序框程序框、流程线、及其功能一、复习算法的三种基本逻辑结构:一、复习(1)顺序结构
由若干个依次执行的步骤组成的。(2)条件结构
算法的流程根据条件是否成立有不同的流向.即先根据条件作出判断, 再决定执行哪一操作的结构.若有A、B、C三个不同大小的数字,你能设计一个算法
找出其中的最大值吗?试给出解决问题的一种算法,
并画出流程图。练习程序框图:作业评讲 P20 3程序框图:算法:(3) 循环结构 在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.直到型循环结构 循环体满足条件?是否当型循环结构满足条件?否是 循环体二、新课算法的三种基本逻辑结构:
当型循环结构先对条件判断,根据结果决定是否执行循环体; 直到型循环结构先执行一次循环体,再对一些条件进行判断,决定是否继续执行循环体.(3) 循环结构二、新课程序框图的三种基本逻辑结构:第1步:0+1=1
第2步:1+2=3
第3步:3+3=6
第4步:6+4=10
……
第100步:4950+100=5050规律:
第i 步:S=S+iS=0,i=1
第1步:S=S+i,
第2步:S=S+i,
第3步:S=S+i,
第4步:S=S+i,
……
第100步:S=S+ii=i+1i=i+1i=i+1i=i+1S=S + ii = i + 1,i=i+1例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。循环步骤:三、例题开始S=0输出S结束i=1i≤100?S=S+ii=i+1框图:算法1:
第一步:取S=0,i=1;
第二步:判断i≤100是否成立 ,
若是,则执行下一步,
若否,则输出S的值;
结束算法
第三步:S=S+i,
第四步: i=i+1,后返回第二步.例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题框图:开始S=0输出S结束i=1i>100?S=S+ii=i+1算法2:
第一步:取S=0,i=1;
第二步:计算S=S+i,i=i+1;
第三步:判断i>100是否成立 ,
若否,则返回第二步,
若是,则输出S的值;例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题当型循环结构直到型循环结构S:累加变量
i:计数变量例6.设计一个计算1+2+3+……+100的值的算法,并画出
程序框图。三、例题变式1:设计一个计算1+2+3+……+100的值的算法,
并画出程序框图。变式2:设计一个计算1+2+3+……+100的值的算法,
并画出程序框图。例7.某工厂2005年的年生产总值为200万元,技术革新后预计以后
每年的年生产总值都比上一年增长5﹪.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.算法:第一步,输入2005年的年生产总值.第二步,计算下一年的年生产总值.第三步,判断所得的结果是否大于
300.若是,则输出该年的年份;否则
返回第二步. 程序框图: a > 300 ?否三、例题 程序框图: a > 300 ?否请将该循环结构改为当型循环例3:写出用“二分法”求方程x2-2=0(x>0)的近似
解的算法第一步:令f(x)=x2-2,给定精确度d第二步:确定区间[a,b],满足f(a)f(b)<0第四步:若f(a)f(m)<0,则含零点的区间为[a,m],否则
含零点的区间为[m,b],将新得到的含零点的
区间仍记为[a,b]第五步:判断[a,b]的长度是否小于d或f(m)是否等于
零,若是,则m是方程的近似解,否则返
回第三步四、程序框图的画法(1).算法步骤中的“第一步”,
“第二步”, “第三步”可以用顺序结构来表示。(2).算法步骤中的
“第四步”,可以
用条件结构来表示。是否 (3).算法步骤中的“第五步”包含一个条件结构,这个条件结构与“第三步”, “第四步”构成一个循环结构。第三步第四步输出m是否 (4).将各步骤的程序框图连接起来,并画出“开始”和
“结束”两个终端框,就得到了表示整个算法的程序框图.设计一个算法的程序框图的步骤:第一步,用自然语言表述算法步骤. 第二步,确定每一个算法步骤所包含的逻辑结构,并用相应的程序框图表示,得到该步骤的程序框图. 第三步,将所有步骤的程序框图用流程线连接起来,并加上终端框,得到表示整个算法的程序框图.是否输出m开始结束是否①①②②的值,并画出程序框图.开始输入一个正整数n输入S的值结束S=0i=1S=S+1/ii=i+1i>n?NY设计一个算法求 思考:将步骤A和步骤B交换位置,结果会怎样?能达到预期结果吗?为什么?要达到预期结果,还需要做怎样的修改?练习: 对任意正整数n,小结1、循环结构的特点2、循环结构的框图表示3、循环结构有注意的问题避免死循环的出现,设置好进入(结束)循环体的条件。当型和直到型重复同一个处理过程习题1.1 A组 第2题
作业1.若已知梯形的上底为a,下底为b,高为h,试设计一个
求该梯形面积的算法,并画出程序框图。
2.设计一个求任意数的绝对值的算法,并画出程序框图。1. 算法:第一步:输入a,b,h的值;第三步:输出梯形的面积S。框图:开始输出S结束输入a,b,h练习2. 算法:第一步:输入x的值;第二步:若x≥0,则输出x;
若否,则输出-x;框图:开始输入xx≥0?输出-x输出x结束1.若已知梯形的上底为a,下底为b,高为h,试设计一个
求该梯形面积的算法,并画出程序框图。
2.设计一个求任意数的绝对值的算法,并画出程序框图。练习
