多边形练习
图片预览



文档简介
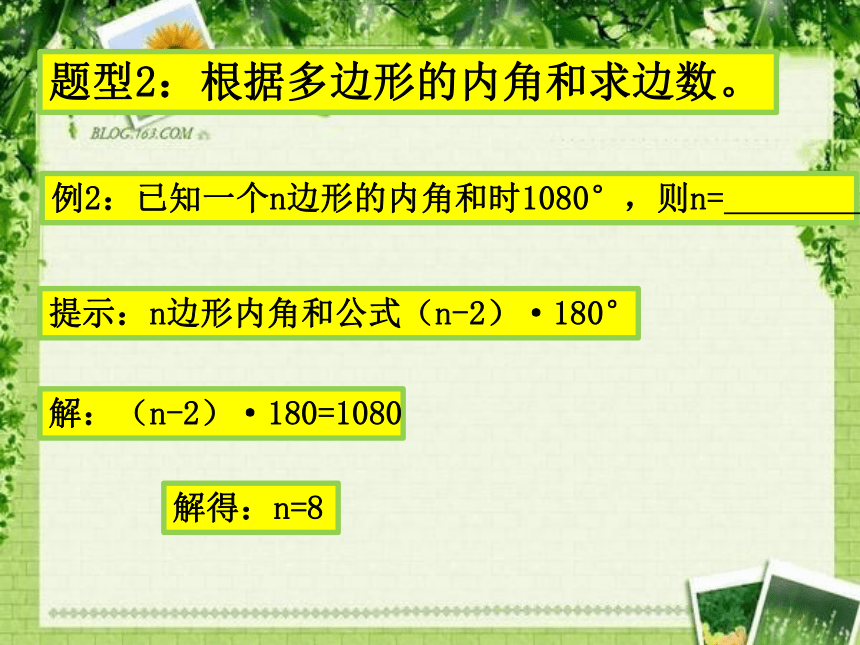
课件10张PPT。多边形重点题型:经典回顾:n边形中,从每一个顶点可引多少条对角线?(n-3)条n边形中,对角线总数为多少?n边形的内角和等于多少?(n-2)·180°n边形外角和等于多少?360°题型1.由边数确定角度。例4.求十一边形的内角和。(11-2)·180°=1620°题型2:根据多边形的内角和求边数。例2:已知一个n边形的内角和时1080°,则n= 提示:n边形内角和公式(n-2)·180°解:(n-2)·180=1080解得:n=8题型3:根据每个外角度数求边数例1.一个正多边形的每个外角都是36°,
这个正多边形的边数是多少?提示:多边形的外角和等于360°。解:360÷36=10题型4:内角与外角的综合运用
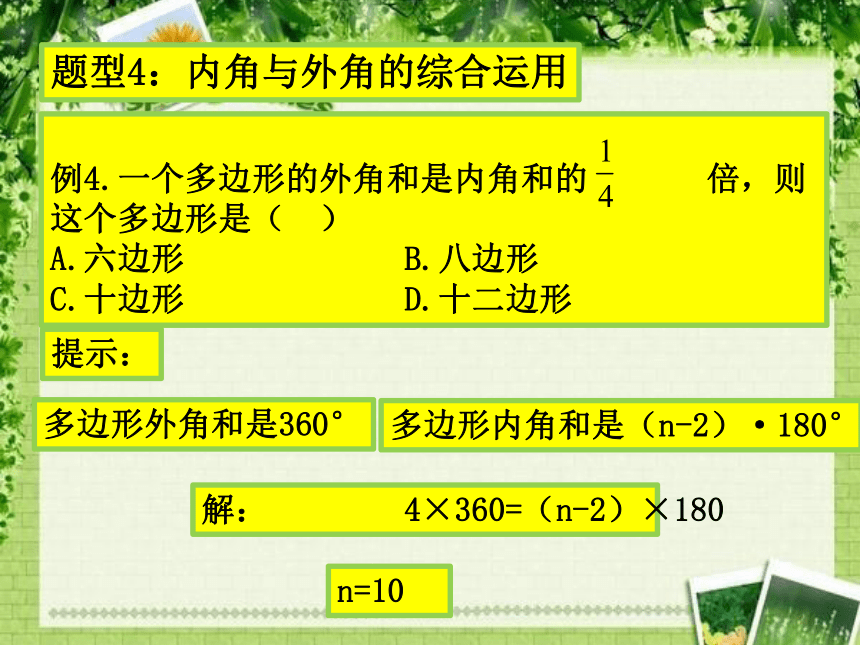
例4.一个多边形的外角和是内角和的 倍,则这个多边形是( )
A.六边形 B.八边形
C.十边形 D.十二边形多边形外角和是360°多边形内角和是(n-2)·180°提示:解: 4×360=(n-2)×180n=10综合运用:例5.一个多边形的每个内角比与它相邻的外角的4倍还多30°,求这个多边形的内角和。解:设这个多边形的一个外角为x°,则与它相邻的内角为(4x+30)°。分析:一个外角和与它相邻的内角互为邻补角,即:x+4x+30=180x=30此多边形的边数为:360÷30=12(12-2)×180°=1800°例6.多边形的外角中,钝角的个数最多有几个?例7.多边形的内角中,锐角的个数最多有几个?3个3个例8.一个n边形有且只有三个内角是钝角,则n的最大值是多少?分析:一个n边形只有三个内角是钝角,即只有三个外角是锐角。其余的外角都是直角或钝角,又因为n边形外角和等于360°,最多还可以有三个直角或钝角,故,n最大值为3+3=6.例9.多边形的内角和与某一个外角的度数总和为1350°,求此多边形的边数。三角形内角和180°四边形内角和五边形内角和六边形内角和七边形内角和八边形内角和360°540°720°900°1080°九边形内角和1260°十边形内角和1440°1260<1350<1440这个外角:
1350°-1260°=90°例9.多边形的内角和与某一个外角的度数总和为1350°,求此多边形的边数。解:设此多边形的边数为n,这个外角的度数为x°。(n-2)×180+x=1350(n-2)×180=1350-xn为整数,故90-x一定是180的倍数,x的取值范围是0
这个正多边形的边数是多少?提示:多边形的外角和等于360°。解:360÷36=10题型4:内角与外角的综合运用
例4.一个多边形的外角和是内角和的 倍,则这个多边形是( )
A.六边形 B.八边形
C.十边形 D.十二边形多边形外角和是360°多边形内角和是(n-2)·180°提示:解: 4×360=(n-2)×180n=10综合运用:例5.一个多边形的每个内角比与它相邻的外角的4倍还多30°,求这个多边形的内角和。解:设这个多边形的一个外角为x°,则与它相邻的内角为(4x+30)°。分析:一个外角和与它相邻的内角互为邻补角,即:x+4x+30=180x=30此多边形的边数为:360÷30=12(12-2)×180°=1800°例6.多边形的外角中,钝角的个数最多有几个?例7.多边形的内角中,锐角的个数最多有几个?3个3个例8.一个n边形有且只有三个内角是钝角,则n的最大值是多少?分析:一个n边形只有三个内角是钝角,即只有三个外角是锐角。其余的外角都是直角或钝角,又因为n边形外角和等于360°,最多还可以有三个直角或钝角,故,n最大值为3+3=6.例9.多边形的内角和与某一个外角的度数总和为1350°,求此多边形的边数。三角形内角和180°四边形内角和五边形内角和六边形内角和七边形内角和八边形内角和360°540°720°900°1080°九边形内角和1260°十边形内角和1440°1260<1350<1440这个外角:
1350°-1260°=90°例9.多边形的内角和与某一个外角的度数总和为1350°,求此多边形的边数。解:设此多边形的边数为n,这个外角的度数为x°。(n-2)×180+x=1350(n-2)×180=1350-xn为整数,故90-x一定是180的倍数,x的取值范围是0
