8.1相交线

课件59张PPT。相交线与平行线第八章8.1相交线

二 三直线相交构成的角三 垂直一 对顶角制作人
07数B 何艳薇学习目标及任务学习目标：1.认识两条直线相交构成的角以及两条直线被第三条直线所截构成的角.
2.学习两条直线相交的特殊情况：垂直相交.学习任务：1.掌握各类角的定义以及位置关系.
2.掌握垂线的作法.
3.学会应用所学知识解决实际问题.？观察与思考图1（1）（2）（3）图中两条直线有什么样的位置关系？有哪些特殊位置关系？不 相 交
相交构成的角均为90度
相 交
OUT2图2一 对顶角
图1的（1）和（2）所示情形，使我们联想到，两条直线相交可以抽象成图2所示的几何图形。
两条直线相交时，形成4个角：∠1，∠2，∠3和∠4。∠1和∠3具有公共点O，并且两边互为反向延长线，我们把这样两个具有特殊位置的角叫做对顶角。 ∠2和∠4也是对顶角。
对顶角的大小有什么关系呢 ？1 .如图2两直线相交于点O,当一条直线饶点O转动时,∠1和∠3同时增大或减小.你能猜出∠1和∠3的大小关系吗?
2.你能用何种方法验证你的猜想?试试看.
3.∠1和∠2互为补角,∠3和∠2互为补角,那么∠1+∠2=( ),∠3+∠2=( ),由此说明∠1和∠3相等吗?通过探究 我们得到如下事实:
对顶角相等KEYS：1.∠1=∠3
2.略
3.180°；180°；能OUT二 同位角 内错角 同旁内角
一条直线C分别与两条直线A,B相交,构成八个角,如图3所示.
观察图3中角与角所处位置之间的关系.
我们把具有∠1和∠5这样位置的一对角叫做同位角。∠2和∠6，∠3和∠7，∠4和∠8也都是同位角。
把具有∠3和∠6这样位置的一对角叫做内错角。∠4和∠5也是内错角。
把具有∠3和∠5这样位置的一对角叫做同旁内角。∠4和∠6也是同旁内角。
大家谈谈各类角各自的位置特征？abc1 23 45 67 8例1 请在图4的基础上分别画出符合下列各条件的角：
1） 与∠ABC是对顶角
2） 与∠ABC是同位角
3） 与∠ABC是内错角
4）与∠ABC是同旁内角图 4BCA∠1
∠2
∠3
∠4
1234例2.直线AB，CD被直线EF所截，交点分别为G，H，所有的同位角，内错角，同旁内角，对顶角各有多少对？分别写出两对来，填入下表。4 ∠AGE与∠FGB
4 ∠AGE与∠AHE
2 ∠BGF与∠CHE
2 ∠AGF与∠CHE例3.如图，已知∠AOC=50°，那么，∠AOD=（ ），∠BOD=（ ），∠BOC=（ ）。
说明理由。CDOBAEABCDFOUT图5图6CAABBOOCDD想一想1.两条直线相交构成四个角,当其中一个是直角时,另外三个角是不是直角?为什么?
2.在一张纸片上画一条直线,你能用折纸的方法AB的垂线吗?
垂线的作法
1).已知直线AB及AB上一点C.
2).已知直线AB及AB外一点C.
?经过直线上或直线外一点画该直线的垂线,可画几条?
事实上,我们有:经过直线上或直线外一点，有且只有一条直线与已知直线垂直。一起探究如图7经过直线AB外一点C画AB的垂线，垂足为D，CD是点C到AB的垂线段。再经过点C向直线AB任意引两条线段CE，CF.
1.观察：线段CE，CD，CF哪一条最短？
2.用刻度尺测量：
CE=（ ）cm，
CD=（ ）cm，
CF=（ ）cm，
这个测量结果能验证你的猜想吗？
3.如图7以点C为圆心，CD的 长为半径画弧，圆弧分别与线段CE，CF相交于点E1,F1.线段CE1,CD,CF1相等吗?为什么?由此能进一步验证你的猜想么?
通过上面的探究,我们认识到这样一个事实:这里线段CD的长度称为点C到直线AB的的距离.图7ABCDEF2.7
2.5
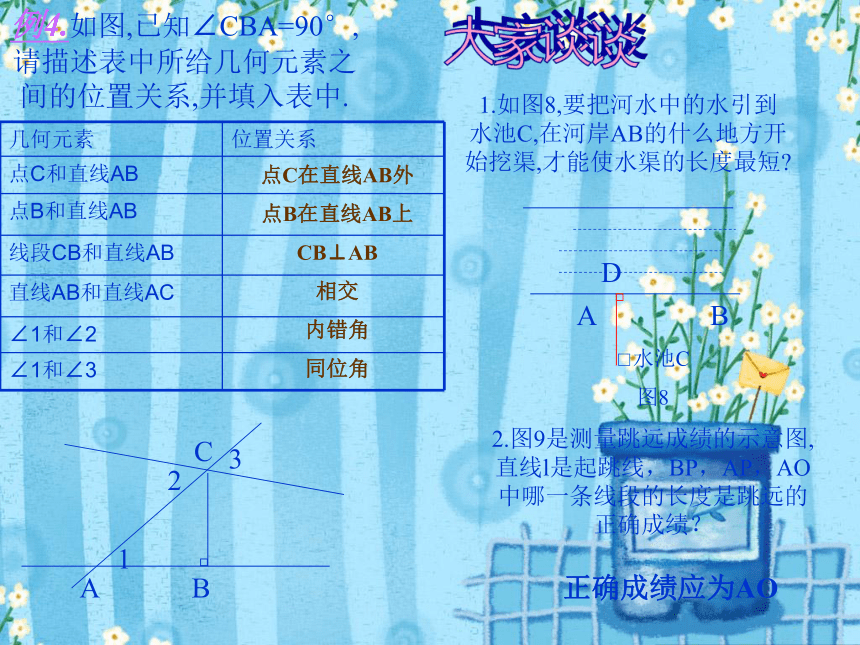
3.4直线外一点与直线上各点连结的所有线段中，垂线 段最短.E1F11.如图8,要把河水中的水引到水池C,在河岸AB的什么地方开始挖渠,才能使水渠的长度最短?A B
□水池C
图8
2.图9是测量跳远成绩的示意图,直线l是起跳线，BP，AP，AO中哪一条线段的长度是跳远的正确成绩？D正确成绩应为AO例4.如图,已知∠CBA=90°,请描述表中所给几何元素之间的位置关系,并填入表中.C231A B点C在直线AB外
点B在直线AB上
CB⊥AB
相交
内错角
同位角大家谈谈再见...See You...OUT主人康斯琪探索直线平行的
条件讲创设情境，导出课题动手操作，探究结论小试牛刀，巩固提高课堂小结，布置作业说课流程你看到了什么样的线呢？？？你注意路的形状了吗？如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行呢?想一想，什么样的位置关系叫作平行？在同一平面内，不相交的两条直线叫做平行线平行线的表示知道了 平行线 的定义了呀
快来和我们一起探究下面的问题吧请你画出一条直线a，并在直线a外任取一点C。你能用上面的方法画出一条过点C且与直线a平行的直线吗？这样的直线能画出多少条？●
C从中你知道
了什么呢？？经过已知直线外一点，有且只有一条直线和已知直线平行继续我们上面的问题哦2.请你观察上面画平行线的过程,将三角尺沿着固定的直尺平推,实际上是为了使直线b和a被直尺边缘所在的直线c所借得什么样的角相等?在已画出的图中，指出这样的角。你认为∠1与∠2满足什么关系时？直线a平行与直线b?
∠1=∠2呀！同位角相等，两直线平行如图是一个正方体
（1）写出三对互相垂直的棱，并用符号表示
（2）写出三对互相平行的棱，并用符号表示
（3）观察棱AB和B1C1，它们所在的直线相交吗？它们所在的直线平行吗？这是为什么？
B1D1A1DC1CBA我们已经知道：同位角相等，两条直线平行。由此，我们联想到：
两条直线被第三条直线所截，能否用内错角或同旁内角之间的关系作为两条直线平行的条件呢？
来看看下面的证明：直线a，b被直线c所截，∠1与∠2是内错角，且∠1=∠2，那么就可以断直线a，b平行。
因为∠1=∠2（已知）
∠1=∠3（对顶角相等）
所以∠2=∠3，a∥b(同位角相等，两直线平行）归纳上面的结论，我们可以得到：内错角相等，两直线平行；
同旁内角互补，两直线平行。快和我去做练习呀例1 如图，∠1=60°，∠2=60°。判断直线a与b是否平行，说明理由。ba例2 如图， ∠A=55°, ∠B=125°,AD与BC平行吗？AB与DC平行吗？为什么？DABC试试吧
小练习
1.如图，直线a，b被直线c所截。已知∠1=110°42′， ∠2=69°18′.直线a,b平行吗？为什么？
2.如图
(1)如果∠1= ∠2,依据 ,可得CD∥EF.
(2）如果 ，根据‘内错角相等，两直线平行，可得CD∥EF
(3)如果 ，根据 ,可得CD∥EF
CA1G43DEF2BH同位角相等同旁内角互补∠2= ∠4∠2= ∠3如图，由∠1=∠2，可以得出的结论是 （ B ）
（A）FG∥BC （B）FG ∥CE
（C）AD ∥CE （D）AD ∥BC小结（1）什么是平行线？怎样表示？
（2）经过已知直线外一点，有且只有一条直线和已知直线平行
（3）同位角相等，两直线平行。
（4）内错角相等，两直线平行；同旁内角相等，两直线平行作业：课后P46，1，2，4，5BYE平行线的特征主讲人：鱼雪红 咱们上节课学的直线平行的条件是什么啊 ?我知道啊 !呵呵!1. 同位角相等,两直线平行.2. 内错角相等,两直线平行.
3. 同旁内角互补,两直线平行.
如下图,a与b平行,其中同位交?1与?5有什么关系啊?1:咱们怎么知道他们的关系啊?测测看行吗? 2:图中还有其它的同位角吗?找找看啊?咱们得到什么结论了,画另一组平行先也会有想同的结论吗?同位角相等这句话对吗? Why?那在什么情况下它们相等呢?我好厉害啊 !我知道了它们相等的条件.两直线平行, 同位角相等.
对呀!好聪明啊!在两条直线平行的情况下,同位角是相等的,那么内错角,同旁内角的关系又如何呢?
我相信你们是最棒的,是不是呀?咱们快来看看啊 !1:图中有几对内错角,它们大小有什么关系?2:图中有几对同旁内角,它们的大小又有什么关系呢? 为什么啊!呵呵!我又知道了平行的两个特征啊!2、两直线平行,内错角相等.
3、两直线平行,同旁内角互补.小试牛刀1:两条直线平行内错角____,同位角____,同旁内角______.2:两条直线被第三条直线所截,则下列说法正确的是( ) (A)同位角相等 B、内错角相等
C、同旁内角互补 D、以上答案都不对
３、∠α和∠β是直线a、b被直线c所截得到的一组同旁内角，且a∥b，若∠α=70 ° ，则∠β=（ ）
(A)70 ° (B)20 °
(C)110 ° (D)不能确定
相等 相等 互补 D C走进生活! 如图:一组平行光AB和DE射向一个水平镜面后被反射,此时∠1=∠2 ， ∠3=∠4 。
⑴∠1、∠3的大小有什么关系?为什么 ?⑵∠２.∠４的大小有什么关系?为什么?⑶发射光线BC与EF也平行吗？
1、如图：直线a、b被直线c所截，且a∥b则，
(1)∵a∥b(已知)，
∴∠1___∠2(?? ? )
(2)∵?____ (已知)，
∴∠2 ＝∠3(? ? )
(3)∵____ (已知)，
∴∠2＋∠4＝____( ? ? ? )2、如图：已知平行线AB、CD被直线AE所截
(1)从∠1＝110°，可以知道∠2是多少度吗？ 为什么？2)从∠1=110°，可以知道∠3是多少度吗？
为什么？(3)从∠1=110°，可以知道∠4是多少度吗？
为什么？ 做一做=两条直线平行，同位角相等。a//b两直线平行,内错角相等.a//b180°两直线平行,同旁内角互补.位于中国四川省广汉市南兴镇北的三星堆遗址，属于古蜀国文明。遗址分布范围达12平方公里，距今4800年至2800年，延续时间近2000年。
　　出土了各种文物：金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。考古走进高考如图：灯塔A在灯塔B的北偏西60 °方向，
则灯塔B在灯塔A的什么方向？ 小结!1:平行线的特征两条直线平行同位角相等内错角相等同旁内角互补2:平行线的特征与判定的关系特征平行关系 角的关系定判角的关系 平行关系作业:教材78业,习题3 , 4 , 5预习下一节的内容. Byebye 第八章 相交线与平行线8.1 相交线
8.2 两直线平行的条件
8.3 平行线的特征
8.4 本章小结要开始复习了哦！！本章小结知识结构
总结与反思
知识结构两条直线相交
1、对顶角
2、垂线对顶角相等
点到直线的距离知识结构两条直线相交
两条直线平行
1、过直线外一点有且只有一条直线和已知直线平行
2、两条直线 平行条件 同位角相等，两直线平行
内错角相等，两直线平行
同旁内角相等，两直线平行 3、平行线的画法4、两直线平
行的特征 两直线平行，同位角等
两直线平行，内错角等
两直线平行，同旁内角相等知识结构两条直线相交
两条直线平行
两条直线被第三条直线所截
注意：同位角、内错角、同旁内角
总结与反思同一平面内两条直线的位置关系只有相交和平行。
两条直线相交，构成四个角，其中有两对对顶角，四对邻补角。
当构成的四个角中有一个是直角时，这两条直线互相垂直。
总结与反思用一条直线去截两条直线，构成八个角，
其中有四对同位角，两对内错角，两对同旁内角。
我们可以借助同位角、
内错角的相等
以及同旁内角的互补
来判定两直线平行总结与反思我们可以用“同位角相等”或“内错角相等”或“同旁内角互补”作为条件来判定两直线平行。
反之如果两直线平行，
那么，同位角相等，
内错角相等，同旁内
角互补总结与反思平行线的画法
我们通常借助三角尺上的直角或量角器画已知垂线的直线；
用移动三角尺的方法画平行线
这是什么原理呢？这实际上是用同位角相等来保证两直线平行总结与反思关于相交线和平行线，有以下基本事实：
1.在同一平面内，经过一点有且仅有一条直线和已知直线垂直
2.直线外一点与直线上各点的连线中，垂线段最短
3.经过直线外一点，有且仅有一条直线和已知直线平行
4.同位角相等，两条直线平行
5.两条直线平行，同位角相等
思考：我们能不能由其他数学事实推出这些结论呢？
我们只可以通过观察画图折纸测量等手段来理解或验证这些事实
不
可
以作业课本P53~P56复习题祝您学习愉快！本章小结结束