解直角三角形应用3

解直角三角形应用3
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一学习目标：
1理解测量中坡度的概念。2能利用解直角三角形的知识解决与坡度 有关的实际问题，进一步培养把实际问题转化为数学问题的能力。
二自主预习：
内容 图形
坡度 坡面的铅垂高度（h）与 （l）的比，叫做坡面的坡度（或坡比），通常用i表示，即i＝ ，表示坡度时，一般把比的前项取作1，写成 的形式。
坡角 与 的夹角叫做坡角，记作α
二者关系 i＝＝ ，坡度i越大，坡角α就 ，坡面就
想一想：坡度就是坡角的度数吗？
三 导学探究：
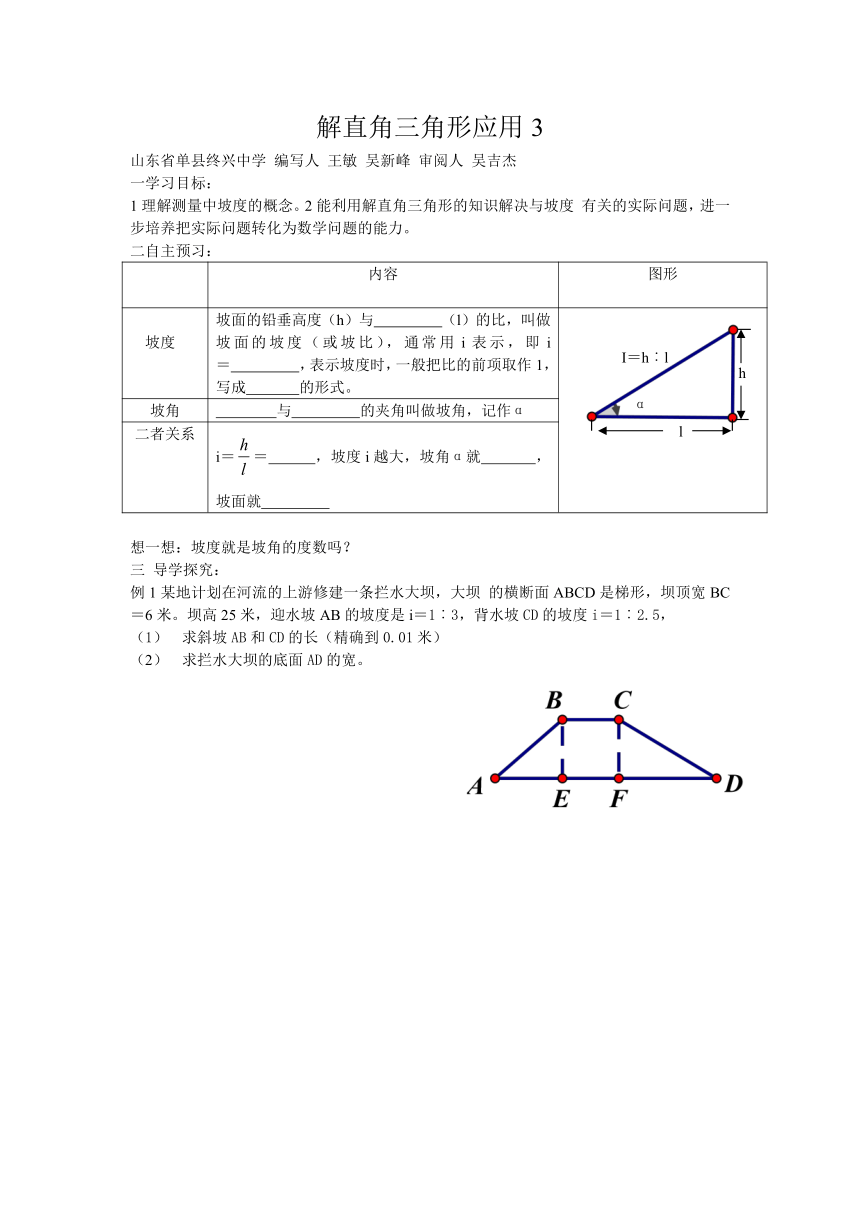
例1某地计划在河流的上游修建一条拦水大坝，大坝 的横断面ABCD是梯形，坝顶宽BC＝6米。坝高25米，迎水坡AB的坡度是i＝1︰3，背水坡CD的坡度i＝1︰2.5，
（1） 求斜坡AB和CD的长（精确到0.01米）
（2） 求拦水大坝的底面AD的宽。
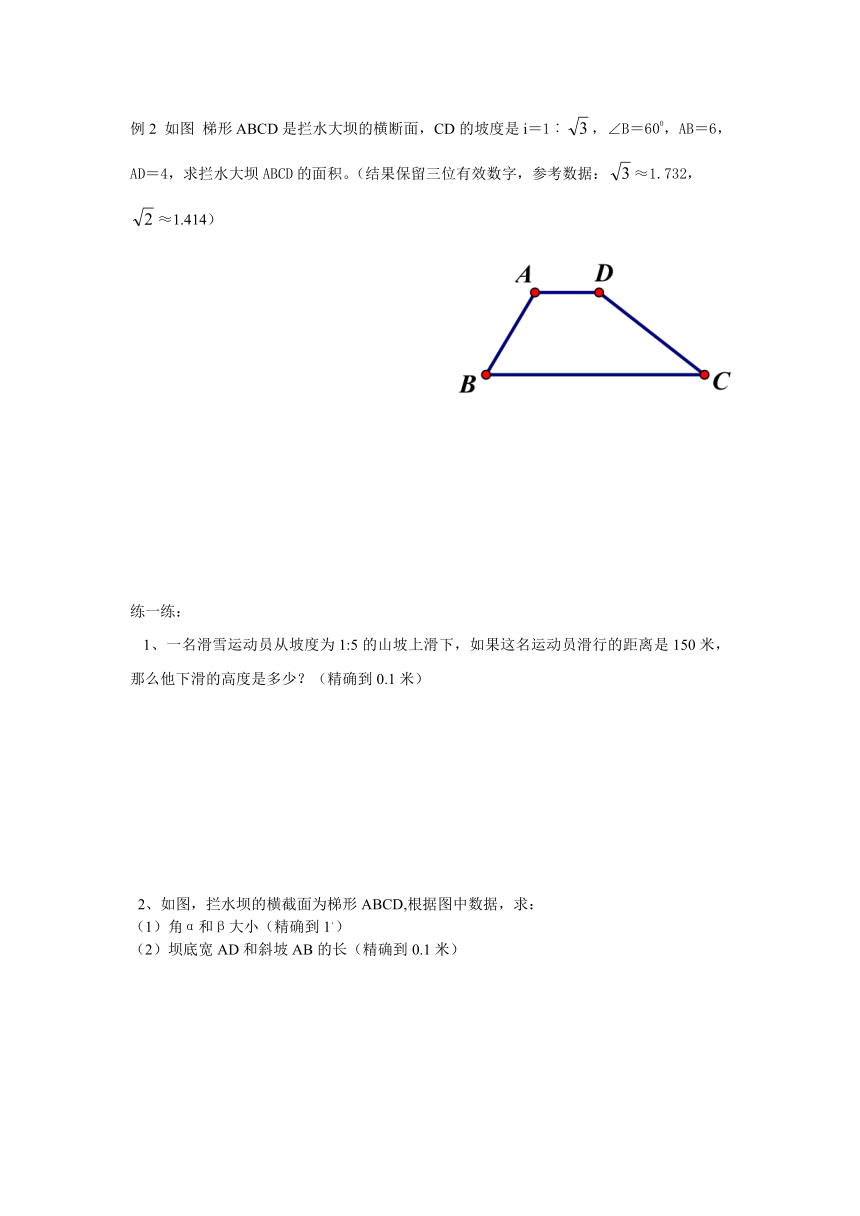
例2 如图 梯形ABCD是拦水大坝的横断面，CD的坡度是i＝1︰，∠B＝600，AB＝6，AD＝4，求拦水大坝ABCD的面积。（结果保留三位有效数字，参考数据：≈1.732，
≈1.414）
练一练：
1、一名滑雪运动员从坡度为1:5的山坡上滑下，如果这名运动员滑行的距离是150米，那么他下滑的高度是多少？（精确到0.1米）
2、如图，拦水坝的横截面为梯形ABCD,根据图中数据，求：
（1）角α和β大小（精确到1，）
（2）坝底宽AD和斜坡AB的长（精确到0.1米）
当堂达标
1 小明沿着坡度为1:2的山坡向上走了1000米，则他升高了（ ）米
A 200 B 500 C 500 D 1000
2 在平地上种植树木时，要求株距（相邻两树间的水平距离）为4米，如果在坡度为0.75米的山坡上种树，也要求株距为4米，那么相邻两树间的坡面距离为（ ）
A 5米 B 6米 C 7米 D 8米
3 如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，引桥坡角∠ABC
为150，则引桥的水平距离BC的长是 米（精确到0.1米）
4 某楼梯的侧面示意图所示，其中AB=4米，∠BAC=300，∠C=900，因某种活动要求铺设红地毯，则在AB段楼梯所铺设红地毯的长度应为 米（结果保留根号）
(2题图） （3题图）
5、（2010.新疆乌鲁木齐）某过街天桥的截面图为梯形，如图所示，其中天桥斜面CD的坡度为i=1:(i=1:是指铅直高度DE与水平宽度CE的比），CD的长为10m,天桥另一斜面AB的坡角∠ABC=450.
（1）写出过街天桥斜面AB的坡度；
（2）求CD的长
(3)若决定对该过街天桥进行改建，使AB斜面的坡度变缓，将其450坡角改为300，方便过路群众，改建后斜面为AF，使计算此改建需占路面FB的长（结果精确到0.01m)
l
h
α
I＝h︰l
I=1:2.5
5.6米
10米
β
α
4米
300