2.4.2平面向量数量积的应用
文档属性
| 名称 | 2.4.2平面向量数量积的应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 800.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-13 00:00:00 | ||
图片预览







文档简介
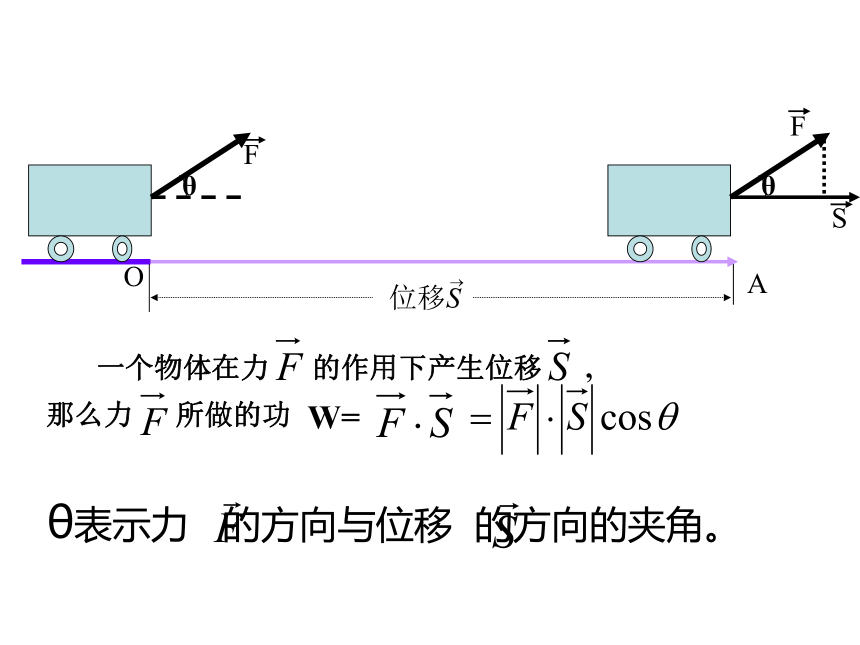
课件23张PPT。2.4.2平面向量数量积的应用 一个物体在力 的作用下产生位移 ,
那么力 所做的功W=θ表示力 的方向与位移 的方向的夹角。一、平面向量数量积的定义:已知两个非零向量 和 ,它们的夹角为? ,
我们把数量 叫做 与 的数量积
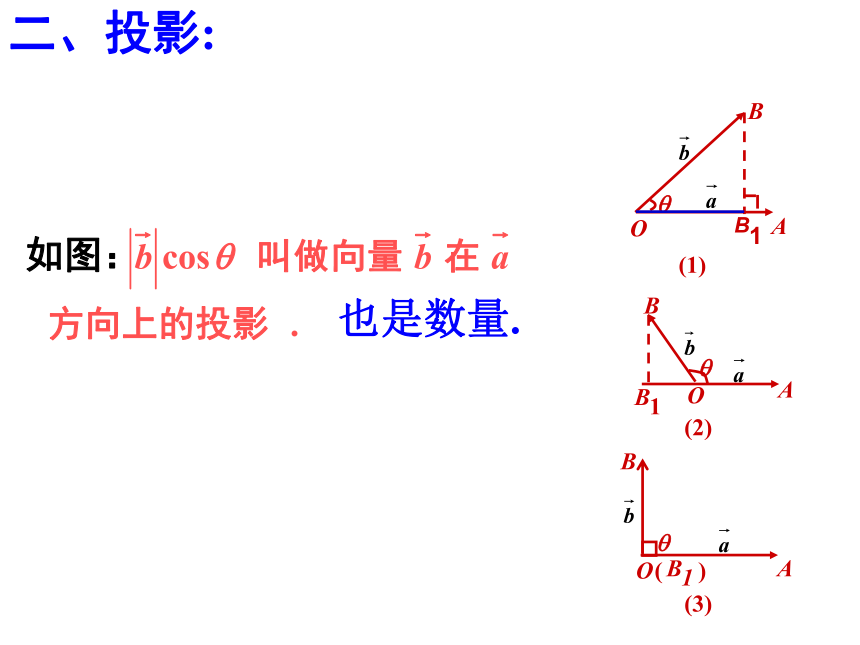
(或内积),记作 .规定:零向量与任意向量的数量积为0.注意: (1) 两个向量的数量积是一个实数,不是向量. (2)两个向量的数量积称为内积,写成 .注意: (3) 向量的数量积和实数与向量的积(数乘)不是一回事. 数量积 的结果是一个数量(实数);实数与向量的积(数乘)还是一个向量.练习:课本 106页 1 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?探究:当0°≤θ<90°时 a·b > 0当90°<θ≤180°时 a·b < 0当θ =90°时 a·b = 0练习:课本 106页 2如图:也是数量.二、投影: 叫做向量 在 方向上(向量 在 方向上)的投影.练习:课本 106页 3 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:三、平面向量数量积的几何意义:四、平面向量数量积的运算率:(1)交换律:(2)数乘结合律: (3)分配律: 数量积不满足结合律和消去率注意:性质判断下列命题是否正确(×)(×)(×)(×)例2.证明:例2.证明:例3 .已知 求解:由题意可知练习: 课本 108页 6练习: 课本 108页 7练习: 课本 108页 3报纸 随堂练习 1,2,3创新 基础测评 1,2
那么力 所做的功W=θ表示力 的方向与位移 的方向的夹角。一、平面向量数量积的定义:已知两个非零向量 和 ,它们的夹角为? ,
我们把数量 叫做 与 的数量积
(或内积),记作 .规定:零向量与任意向量的数量积为0.注意: (1) 两个向量的数量积是一个实数,不是向量. (2)两个向量的数量积称为内积,写成 .注意: (3) 向量的数量积和实数与向量的积(数乘)不是一回事. 数量积 的结果是一个数量(实数);实数与向量的积(数乘)还是一个向量.练习:课本 106页 1 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?探究:当0°≤θ<90°时 a·b > 0当90°<θ≤180°时 a·b < 0当θ =90°时 a·b = 0练习:课本 106页 2如图:也是数量.二、投影: 叫做向量 在 方向上(向量 在 方向上)的投影.练习:课本 106页 3 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:三、平面向量数量积的几何意义:四、平面向量数量积的运算率:(1)交换律:(2)数乘结合律: (3)分配律: 数量积不满足结合律和消去率注意:性质判断下列命题是否正确(×)(×)(×)(×)例2.证明:例2.证明:例3 .已知 求解:由题意可知练习: 课本 108页 6练习: 课本 108页 7练习: 课本 108页 3报纸 随堂练习 1,2,3创新 基础测评 1,2
