直线和圆的位置关系复习课件
文档属性
| 名称 | 直线和圆的位置关系复习课件 |  | |
| 格式 | rar | ||
| 文件大小 | 43.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-13 22:07:00 | ||
图片预览

文档简介
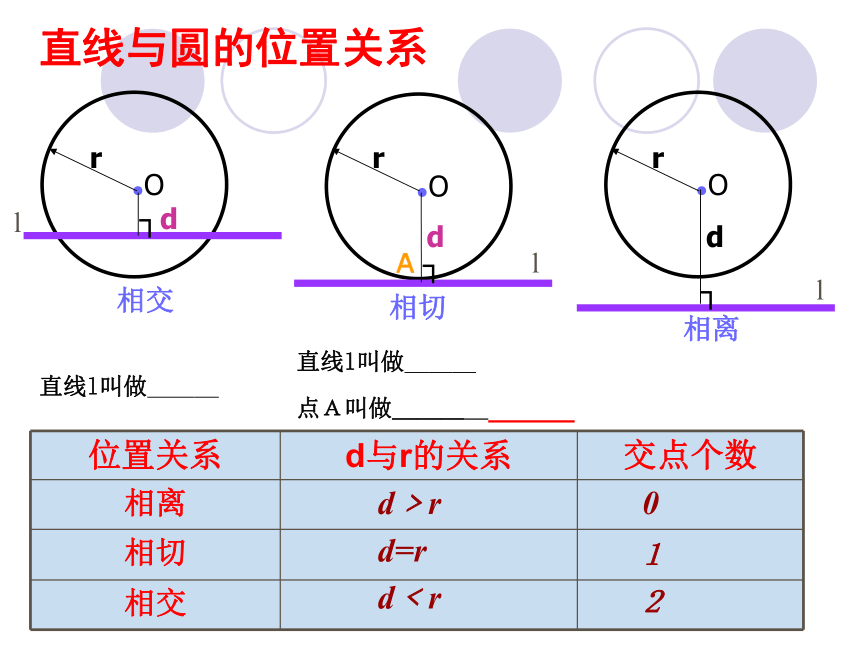
课件12张PPT。直线和圆的位置关系复习课两道桥中学 鄢俊华直线与圆的位置关系lllA直线l叫做___ 直线l叫做___
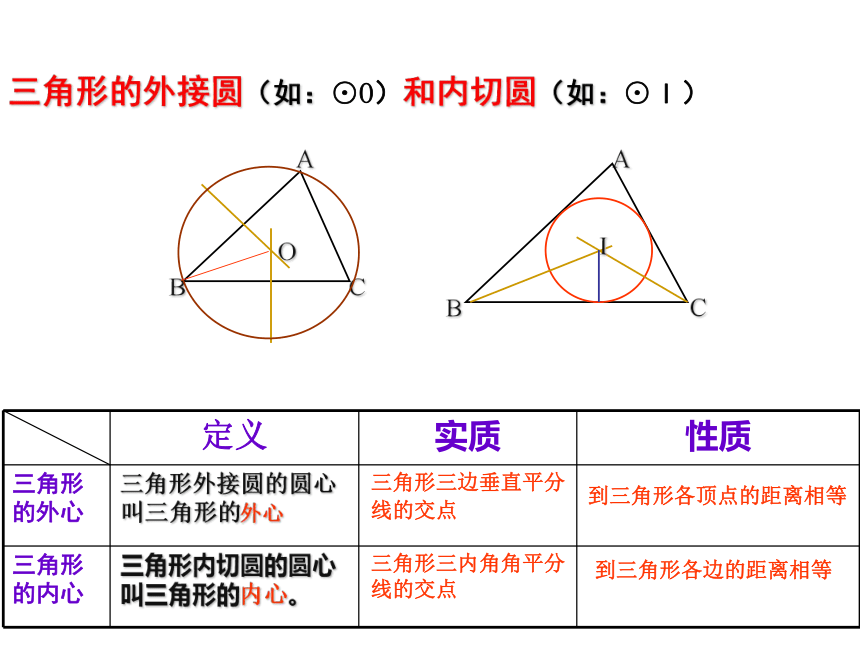
点A叫做___ d﹥rd=rd﹤r012三角形的外接圆(如:⊙O)和内切圆(如:⊙I) 三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等
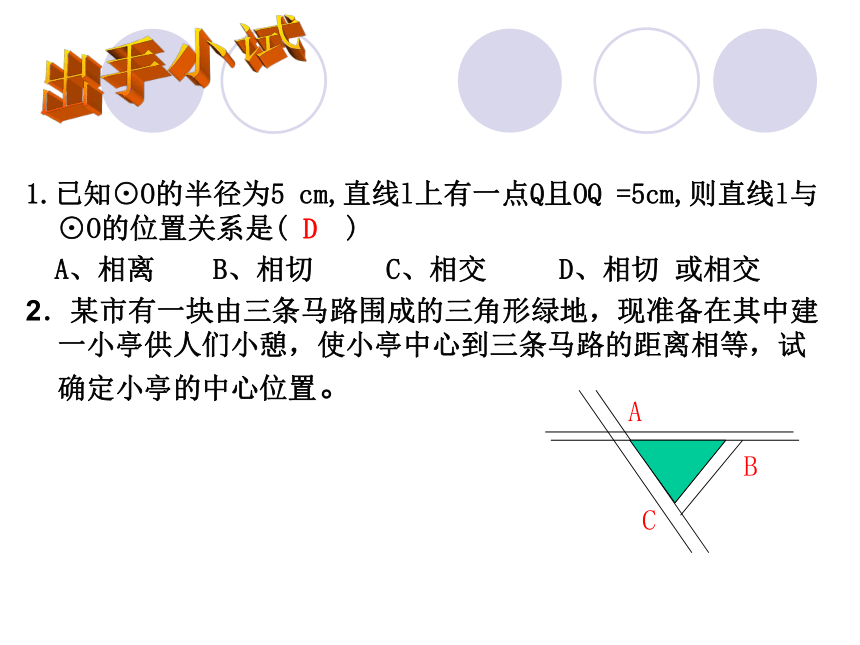
1.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切 或相交
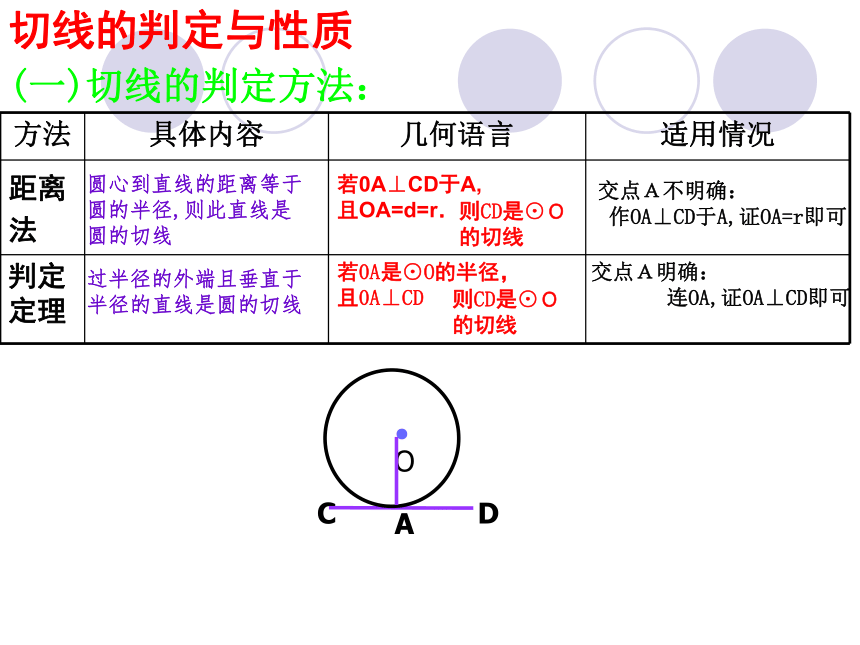
2.某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭的中心位置。出手小试D切线的判定与性质(一)切线的判定方法:距离
法
判定
定理圆心到直线的距离等于
圆的半径,则此直线是
圆的切线过半径的外端且垂直于
半径的直线是圆的切线若0A⊥CD于A,且OA=d=r.则CD是⊙O
的切线交点A明确:
连OA,证OA⊥CD即可交点A不明确:
作OA⊥CD于A,证OA=r即可若0A是⊙O的半径,
且0A⊥CD则CD是⊙O
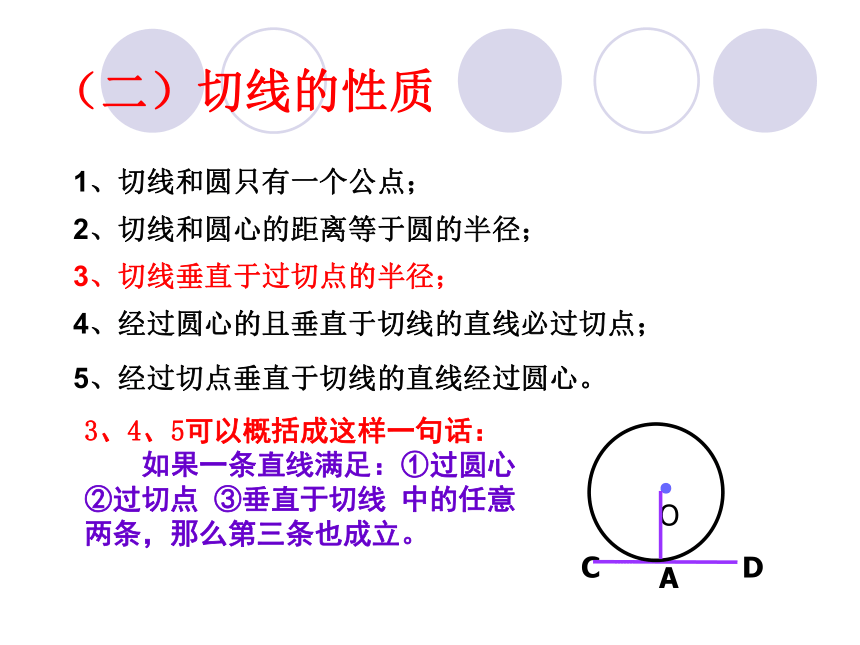
的切线(二)切线的性质
1、切线和圆只有一个公点;2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;4、经过圆心的且垂直于切线的直线必过切点;5、经过切点垂直于切线的直线经过圆心。3、4、5可以概括成这样一句话:
如果一条直线满足:①过圆心
②过切点 ③垂直于切线 中的任意
两条,那么第三条也成立。1.如图1,△ABC中,AB=AC,O是BC的中点,以O为
圆心的圆与AB相切于点D,
求证:AC是圆的切线
2.如图2,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
下列两题,你会分别选择哪种方法判断其为切线?(距离法)(判定定理)从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.七:切线长定理八:直角三角形的内切圆半径
与三边关系.几何语言:若PA,PB切⊙O于A,B 1.一个基本图形; 2.两个结论(1)四边形OECF是正方形(2)① r=(a+b-c) ÷2
② r=ab ÷(a+b+c)3.两个方法(1)代数法(方程思想)(2)面积法则①PA=PB ②∠1=∠21.如图,圆O切PB于点B,PB=4,PA=2,则圆O的半径是____.
2.在直角三角形ABC中, ∠C=90度,AC=6,BC=8,则其外接圆半径=___, 内切圆半径=___.
352再来一手O 例 如图4,⊙M与x轴相交于点A(2,0),
B(8,0),与y轴相切于点C,
求圆心M的坐标.例题讲解D解:如图,AB=OB-OA=8-2=6,
过M作MD⊥AB于D,则AD=3,
∴OD=5,
连结CM则CM⊥OC,
∵CO⊥OD,
∴四边形ODMC是矩形,
∴MC=OD=5,
连结AM,则AM=MC=5
∴MD= =4
∴M(5,4)练习题:
据报道 :我国探月“嫦娥计划”第一颗卫星“嫦娥一号”
已定于10 月24日发射.
听到这则新闻,大大激发了王坤同学爱好天文的热情.他通过上网查阅资料了解到.地球和金星的运行轨道可以近似地看着以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示).由于金星和地球运转速度不同,所以两者的位置不断地发生变化:
当金星,地球距离最近时,此时叫“下合”
当金星,地球距离最远时,此时叫“上合”
在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”.
已知地球与太阳相距约15(千万km),金星与太阳相距约10(千万km),
分别求“下合” ,“东大距”,“西大距”,“上合”时,金星与地球的距离.
(可用根号表示) 课 堂 小 结
点A叫做___ d﹥rd=rd﹤r012三角形的外接圆(如:⊙O)和内切圆(如:⊙I) 三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等
1.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切 或相交
2.某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭的中心位置。出手小试D切线的判定与性质(一)切线的判定方法:距离
法
判定
定理圆心到直线的距离等于
圆的半径,则此直线是
圆的切线过半径的外端且垂直于
半径的直线是圆的切线若0A⊥CD于A,且OA=d=r.则CD是⊙O
的切线交点A明确:
连OA,证OA⊥CD即可交点A不明确:
作OA⊥CD于A,证OA=r即可若0A是⊙O的半径,
且0A⊥CD则CD是⊙O
的切线(二)切线的性质
1、切线和圆只有一个公点;2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;4、经过圆心的且垂直于切线的直线必过切点;5、经过切点垂直于切线的直线经过圆心。3、4、5可以概括成这样一句话:
如果一条直线满足:①过圆心
②过切点 ③垂直于切线 中的任意
两条,那么第三条也成立。1.如图1,△ABC中,AB=AC,O是BC的中点,以O为
圆心的圆与AB相切于点D,
求证:AC是圆的切线
2.如图2,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
下列两题,你会分别选择哪种方法判断其为切线?(距离法)(判定定理)从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.七:切线长定理八:直角三角形的内切圆半径
与三边关系.几何语言:若PA,PB切⊙O于A,B 1.一个基本图形; 2.两个结论(1)四边形OECF是正方形(2)① r=(a+b-c) ÷2
② r=ab ÷(a+b+c)3.两个方法(1)代数法(方程思想)(2)面积法则①PA=PB ②∠1=∠21.如图,圆O切PB于点B,PB=4,PA=2,则圆O的半径是____.
2.在直角三角形ABC中, ∠C=90度,AC=6,BC=8,则其外接圆半径=___, 内切圆半径=___.
352再来一手O 例 如图4,⊙M与x轴相交于点A(2,0),
B(8,0),与y轴相切于点C,
求圆心M的坐标.例题讲解D解:如图,AB=OB-OA=8-2=6,
过M作MD⊥AB于D,则AD=3,
∴OD=5,
连结CM则CM⊥OC,
∵CO⊥OD,
∴四边形ODMC是矩形,
∴MC=OD=5,
连结AM,则AM=MC=5
∴MD= =4
∴M(5,4)练习题:
据报道 :我国探月“嫦娥计划”第一颗卫星“嫦娥一号”
已定于10 月24日发射.
听到这则新闻,大大激发了王坤同学爱好天文的热情.他通过上网查阅资料了解到.地球和金星的运行轨道可以近似地看着以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示).由于金星和地球运转速度不同,所以两者的位置不断地发生变化:
当金星,地球距离最近时,此时叫“下合”
当金星,地球距离最远时,此时叫“上合”
在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”.
已知地球与太阳相距约15(千万km),金星与太阳相距约10(千万km),
分别求“下合” ,“东大距”,“西大距”,“上合”时,金星与地球的距离.
(可用根号表示) 课 堂 小 结
同课章节目录
