2.4.2 平面向量数量积的坐标表示、模、夹角
文档属性
| 名称 | 2.4.2 平面向量数量积的坐标表示、模、夹角 |

|
|
| 格式 | rar | ||
| 文件大小 | 670.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-17 00:00:00 | ||
图片预览






文档简介
课件17张PPT。2.4.2 平面向量数量积的坐标表示、模、夹角一、复习引入 我们学过两向量的和与差可以转化为它们相应的坐标来运算,那么怎样用下面研究怎样用设两个非零向量 =(x1,y1), =(x2,y2),则
故两个向量的数量积等于它们对应坐标的乘积的和。即
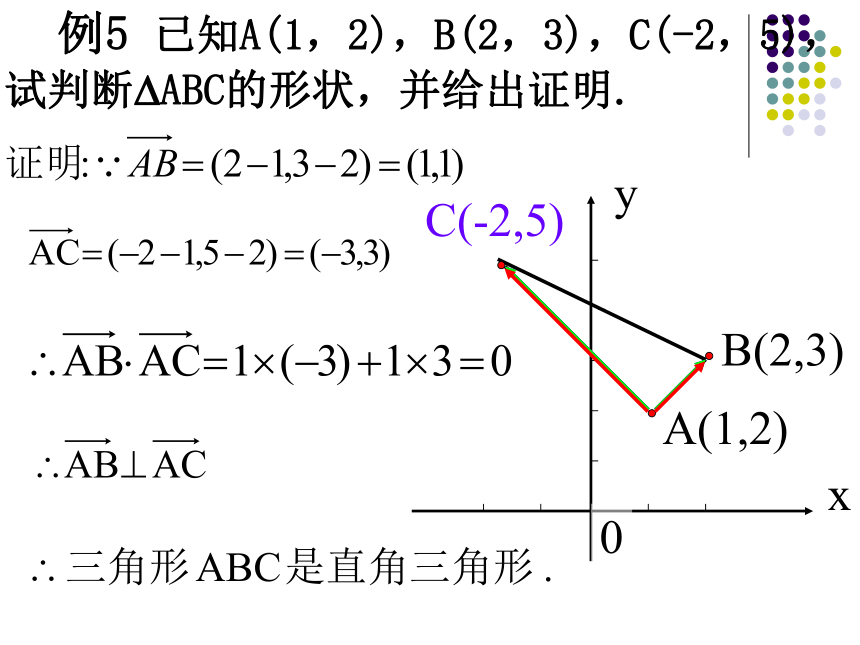
根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。2、向量的模和两点间的距离公式(1)垂直3、两向量垂直和平行的坐标表示(2)平行 例5 已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.C(-2,5)练习:课本 107页 1,2练习:课本 107页 1,2练习:课本 108页 10练习:课本 108页 9练习:课本 108页 9练习:课本 108页 4(5班的)4、两向量夹角公式的坐标运算解:≈0.0322413θ=arccos0.0322413≈88°创新 基础测评 1~4报纸 随堂练习 3报纸 随堂练习 1报纸 随堂练习 2
故两个向量的数量积等于它们对应坐标的乘积的和。即
根据平面向量数量积的坐标表示,向量的数量积的运算可转化为向量的坐标运算。2、向量的模和两点间的距离公式(1)垂直3、两向量垂直和平行的坐标表示(2)平行 例5 已知A(1,2),B(2,3),C(-2,5),试判断?ABC的形状,并给出证明.C(-2,5)练习:课本 107页 1,2练习:课本 107页 1,2练习:课本 108页 10练习:课本 108页 9练习:课本 108页 9练习:课本 108页 4(5班的)4、两向量夹角公式的坐标运算解:≈0.0322413θ=arccos0.0322413≈88°创新 基础测评 1~4报纸 随堂练习 3报纸 随堂练习 1报纸 随堂练习 2
