三角形的内角和学案
图片预览
文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
7.2.1三角形的内角和学案
学习目标
1 会用不同的方法证明三角形的内角和定理,同时证明外角的两个性质,得出三角形外角和。
2 能应用三角形内角和定理和外角的性质解决一些简单的问题
3、培养学生合作探究的能力。
1、 学一学,自学教材P72---77(用红笔标注重点,尝试将课后练习和P77习题写在书上)
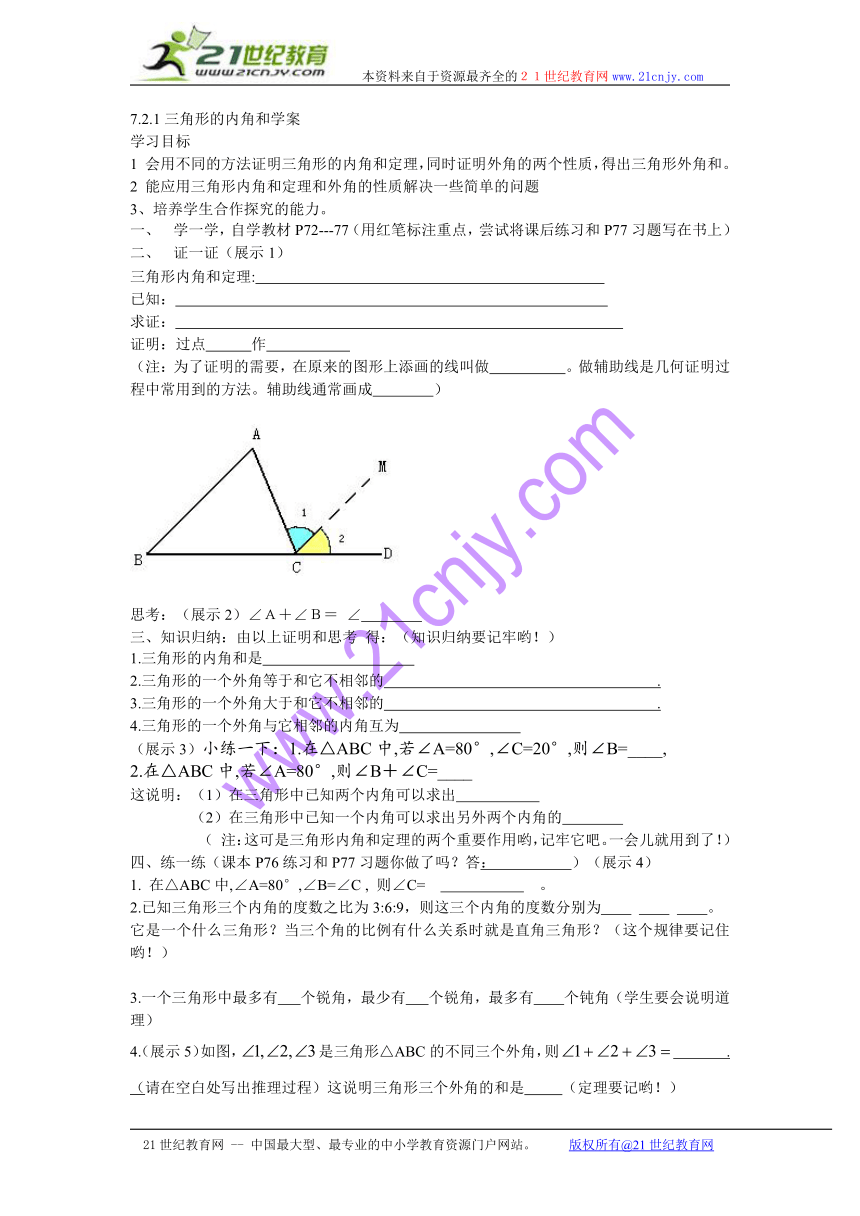
2、 证一证(展示1)
三角形内角和定理:
已知:
求证:
证明:过点 作
(注:为了证明的需要,在原来的图形上添画的线叫做 。做辅助线是几何证明过程中常用到的方法。辅助线通常画成 )
思考:(展示2)∠A+∠B= ∠
三、知识归纳:由以上证明和思考 得:(知识归纳要记牢哟!)
1.三角形的内角和是
2.三角形的一个外角等于和它不相邻的 .
3.三角形的一个外角大于和它不相邻的 .
4.三角形的一个外角与它相邻的内角互为
(展示3)小练一下:1.在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
2.在△ABC中,若∠A=80°,则∠B+∠C=____
这说明:(1)在三角形中已知两个内角可以求出
(2)在三角形中已知一个内角可以求出另外两个内角的
( 注:这可是三角形内角和定理的两个重要作用哟,记牢它吧。一会儿就用到了!)
四、练一练(课本P76练习和P77习题你做了吗?答: )(展示4)
1. 在△ABC中,∠A=80°,∠B=∠C , 则∠C= 。
2.已知三角形三个内角的度数之比为3:6:9,则这三个内角的度数分别为 。
它是一个什么三角形?当三个角的比例有什么关系时就是直角三角形?(这个规律要记住哟!)
3.一个三角形中最多有 个锐角,最少有 个锐角,最多有 个钝角(学生要会说明道理)
4.(展示5)如图,是三角形△ABC的不同三个外角,则 .(请在空白处写出推理过程)这说明三角形三个外角的和是 (定理要记哟!)
五、(展示6)例题 如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
(先独立解决,再小组合作,教师点评)
六(展示7)总结本节所学的重要知识点和重要方法
当堂测评(展示8)
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
若∠A=80°,∠B=∠C,则∠C=____。
2、已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,
则∠B=____,∠C=____。
3、如图,在△ABC中∠C=60°,∠B=50°,
AD是∠BAC的平分线,则∠BAD= ∠DAC=_ ___,
∠ADB=_____。
4、在△ABC中,∠B,∠C的平分线交于点O,
若∠BOC=132°,则∠A=______.若∠BOC=a°则∠A=______
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
7.2.1三角形的内角和学案
学习目标
1 会用不同的方法证明三角形的内角和定理,同时证明外角的两个性质,得出三角形外角和。
2 能应用三角形内角和定理和外角的性质解决一些简单的问题
3、培养学生合作探究的能力。
1、 学一学,自学教材P72---77(用红笔标注重点,尝试将课后练习和P77习题写在书上)
2、 证一证(展示1)
三角形内角和定理:
已知:
求证:
证明:过点 作
(注:为了证明的需要,在原来的图形上添画的线叫做 。做辅助线是几何证明过程中常用到的方法。辅助线通常画成 )
思考:(展示2)∠A+∠B= ∠
三、知识归纳:由以上证明和思考 得:(知识归纳要记牢哟!)
1.三角形的内角和是
2.三角形的一个外角等于和它不相邻的 .
3.三角形的一个外角大于和它不相邻的 .
4.三角形的一个外角与它相邻的内角互为
(展示3)小练一下:1.在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
2.在△ABC中,若∠A=80°,则∠B+∠C=____
这说明:(1)在三角形中已知两个内角可以求出
(2)在三角形中已知一个内角可以求出另外两个内角的
( 注:这可是三角形内角和定理的两个重要作用哟,记牢它吧。一会儿就用到了!)
四、练一练(课本P76练习和P77习题你做了吗?答: )(展示4)
1. 在△ABC中,∠A=80°,∠B=∠C , 则∠C= 。
2.已知三角形三个内角的度数之比为3:6:9,则这三个内角的度数分别为 。
它是一个什么三角形?当三个角的比例有什么关系时就是直角三角形?(这个规律要记住哟!)
3.一个三角形中最多有 个锐角,最少有 个锐角,最多有 个钝角(学生要会说明道理)
4.(展示5)如图,是三角形△ABC的不同三个外角,则 .(请在空白处写出推理过程)这说明三角形三个外角的和是 (定理要记哟!)
五、(展示6)例题 如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
(先独立解决,再小组合作,教师点评)
六(展示7)总结本节所学的重要知识点和重要方法
当堂测评(展示8)
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
若∠A=80°,∠B=∠C,则∠C=____。
2、已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,
则∠B=____,∠C=____。
3、如图,在△ABC中∠C=60°,∠B=50°,
AD是∠BAC的平分线,则∠BAD= ∠DAC=_ ___,
∠ADB=_____。
4、在△ABC中,∠B,∠C的平分线交于点O,
若∠BOC=132°,则∠A=______.若∠BOC=a°则∠A=______
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
