第15章三角形的全等三角形全等的判定
图片预览

文档简介
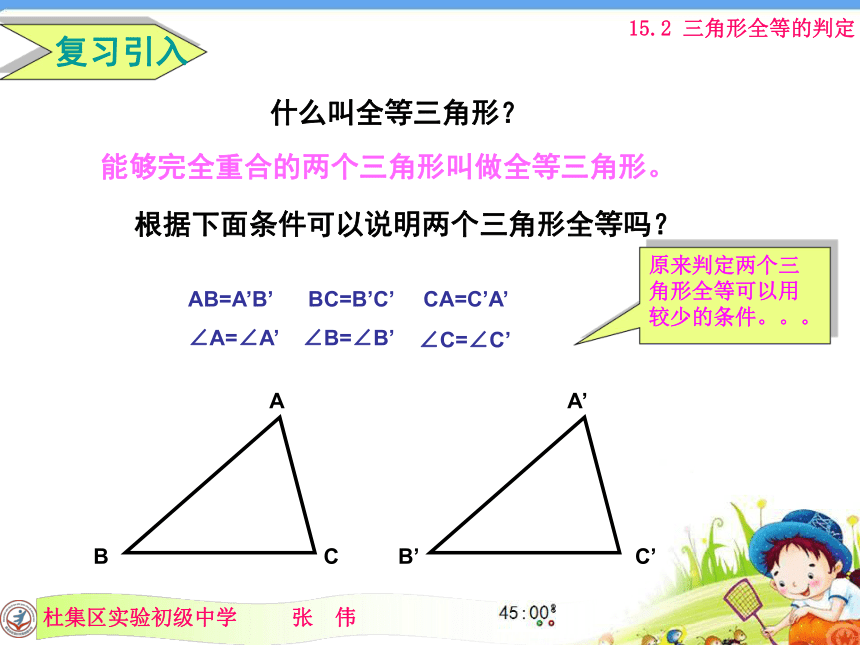
课件20张PPT。什么叫全等三角形? 复习引入能够完全重合的两个三角形叫做全等三角形。根据下面条件可以说明两个三角形全等吗?ACBAB=A’B’ BC=B’C’ CA=C’A’
∠A=∠A’ ∠B=∠B’∠C=∠C’原来判定两个三角形全等可以用较少的条件。。。15.2 三角形全等的判定第一组:一条边为4cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和5cm;
第四组:两个角分别为45°和60°;
第五组:一条边为4cm,一个角为45°。
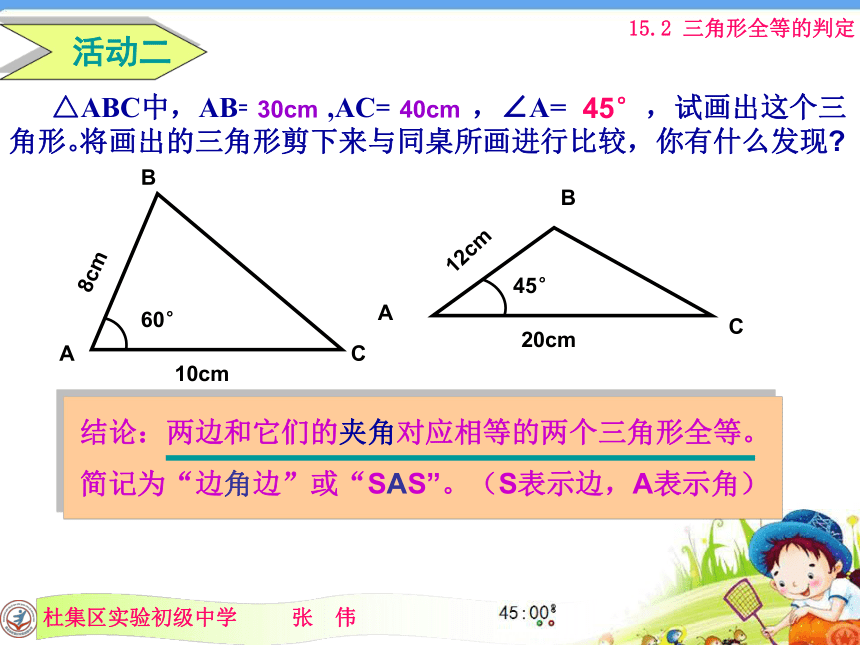
按下列条件做出的三角形是否全等呢? 活动一只给定三角形的一个元素只给定三角形的两个元素动画动画动画动画动画通过以上操作观察,你有什么发现? △ABC中,AB= 8cm ,AC= 10cm ,∠A= 60°,试画出这个三角形。 活动二结论:两边和它们的夹角对应相等的两个三角形全等。
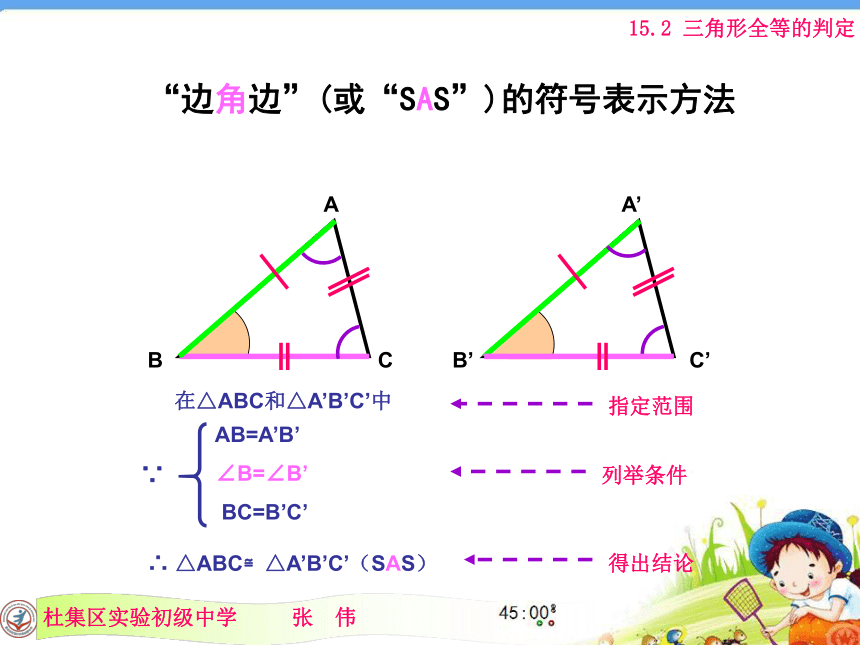
简记为“边角边”或“SAS”。(S表示边,A表示角)将画出的三角形剪下来与同桌所画进行比较,你有什么发现?45°20cm12cm40cm30cm“边角边”(或“SAS”)的符号表示方法ACB AB=A’B’
∠B=∠B’
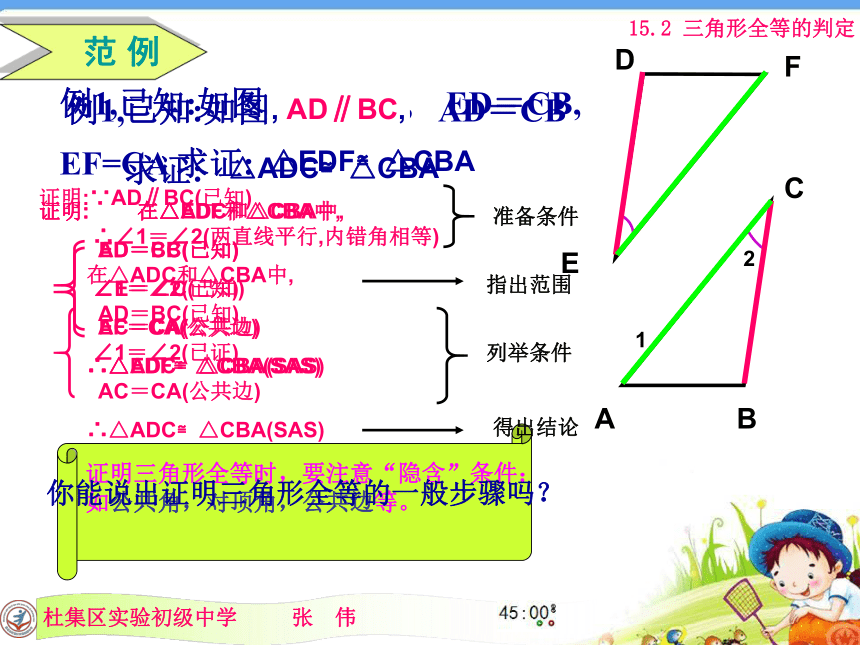
BC=B’C’∵在△ABC和△A’B’C’中∴ △ABC≌△A’B’C’(SAS)指定范围列举条件得出结论例1,已知:如图,∠E=∠C, ED=CB,
EF=CA 求证:证明: 在△EDF和△CBA中,
ED=CB(已知)
∠E=∠C(已知)
EF=CA(公共边)
∴△EDF≌△CBA(SAS)△EDF≌△CBAABCD 范 例12FE证明: 在△ADC和△CBA中,
AD=BC(已知)
∠1=∠2(已知)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)例1,已知:如图,∠1=∠2, AD=CB
求证:△ADC≌△CBA证明三角形全等时,要注意“隐含”条件:
如公共角,对顶角,公共边等。
, AD∥BC,准备条件指出范围列举条件得出结论你能说出证明三角形全等的一般步骤吗?证明:∵AD∥BC(已知)
∴∠1=∠2(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠1=∠2(已证)
AC=CA(公共边)
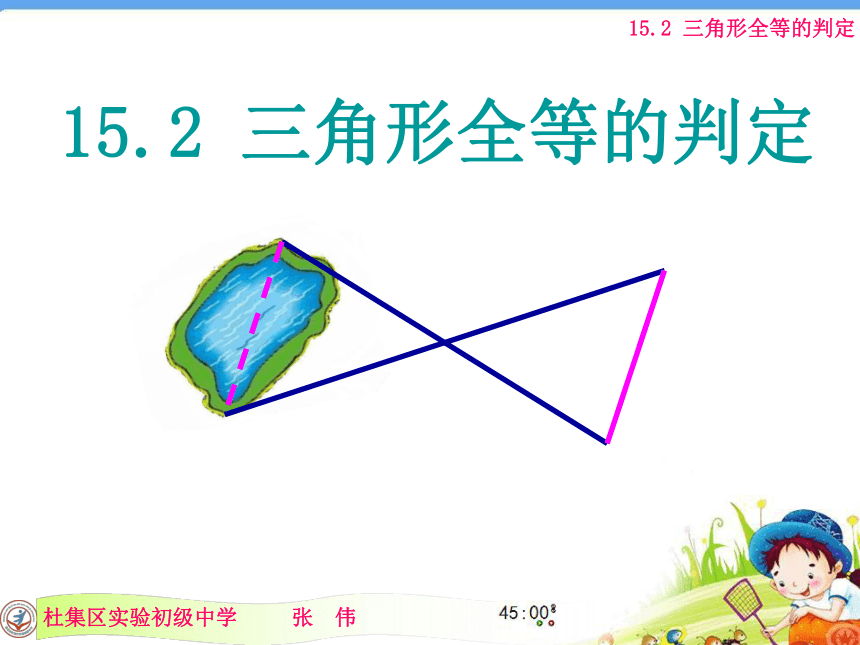
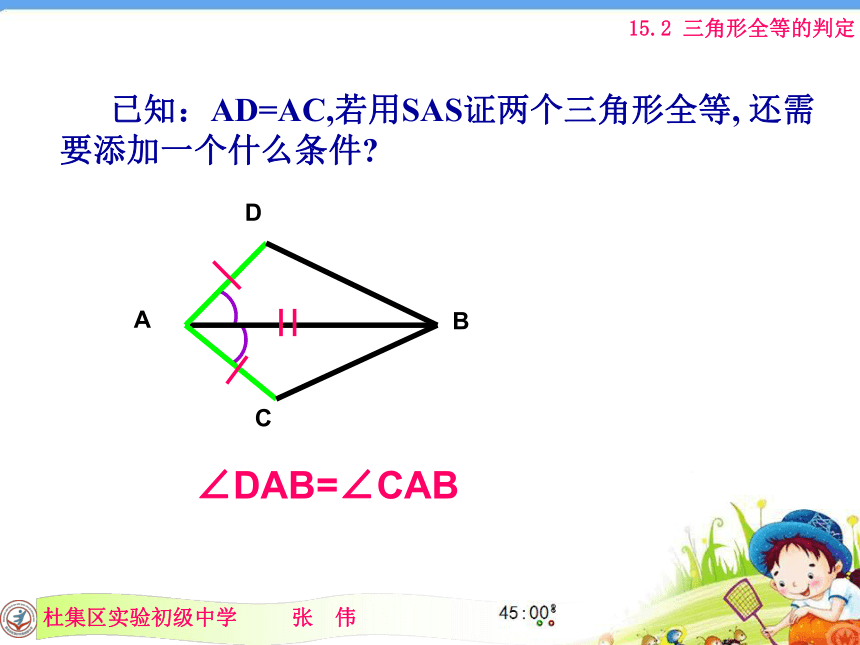
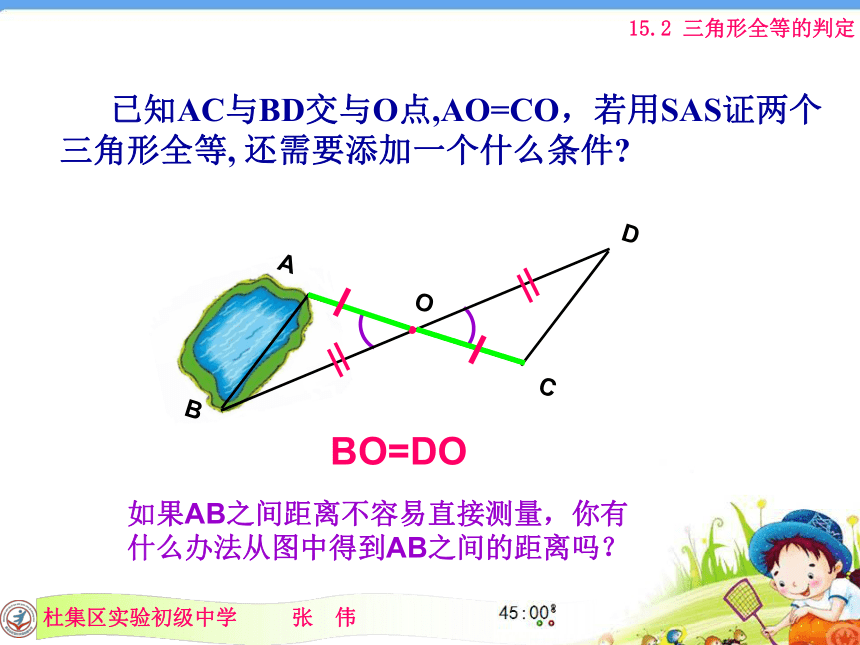
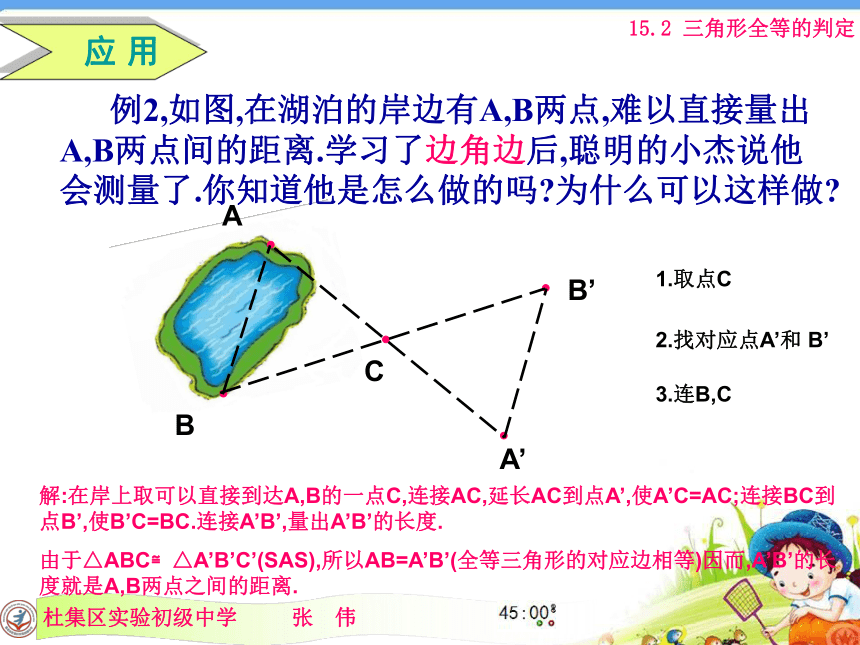
∴△ADC≌△CBA(SAS) 已知:AD=AC,若用SAS证两个三角形全等, 还需要添加一个什么条件?∠DAB=∠CAB 已知AC与BD交与O点,AO=CO,若用SAS证两个三角形全等, 还需要添加一个什么条件?BO=DO如果AB之间距离不容易直接测量,你有什么办法从图中得到AB之间的距离吗? 例2,如图,在湖泊的岸边有A,B两点,难以直接量出A,B两点间的距离.学习了边角边后,聪明的小杰说他会测量了.你知道他是怎么做的吗?为什么可以这样做?ABCA’B’解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A’,使A’C=AC;连接BC到点B’,使B’C=BC.连接A’B’,量出A’B’的长度.
由于△ABC≌△A’B’C’(SAS),所以AB=A’B’(全等三角形的对应边相等)因而,A’B’的长度就是A,B两点之间的距离. 应 用1.取点C2.找对应点A’和 B’3.连B,C1.学习了本节课以后,你有哪些收获?
2.你还有什么疑惑? 小 结 学习本节课后,我们知道已知两边及其夹角这三对元素对应相等,就可以判断两三角形全等,那么两个三角形具备其他三组元素对应相等,他们是否也能得到两个三角形全等呢? 思考课本95页,练习第1,2题 作 业谢谢! △ABC中,AB=4cm,AC=5cm,∠A=60°,试画出这个三角形。 活动三ABC4cm5cm60°△ABC就是所求图形
∠A=∠A’ ∠B=∠B’∠C=∠C’原来判定两个三角形全等可以用较少的条件。。。15.2 三角形全等的判定第一组:一条边为4cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和5cm;
第四组:两个角分别为45°和60°;
第五组:一条边为4cm,一个角为45°。
按下列条件做出的三角形是否全等呢? 活动一只给定三角形的一个元素只给定三角形的两个元素动画动画动画动画动画通过以上操作观察,你有什么发现? △ABC中,AB= 8cm ,AC= 10cm ,∠A= 60°,试画出这个三角形。 活动二结论:两边和它们的夹角对应相等的两个三角形全等。
简记为“边角边”或“SAS”。(S表示边,A表示角)将画出的三角形剪下来与同桌所画进行比较,你有什么发现?45°20cm12cm40cm30cm“边角边”(或“SAS”)的符号表示方法ACB AB=A’B’
∠B=∠B’
BC=B’C’∵在△ABC和△A’B’C’中∴ △ABC≌△A’B’C’(SAS)指定范围列举条件得出结论例1,已知:如图,∠E=∠C, ED=CB,
EF=CA 求证:证明: 在△EDF和△CBA中,
ED=CB(已知)
∠E=∠C(已知)
EF=CA(公共边)
∴△EDF≌△CBA(SAS)△EDF≌△CBAABCD 范 例12FE证明: 在△ADC和△CBA中,
AD=BC(已知)
∠1=∠2(已知)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)例1,已知:如图,∠1=∠2, AD=CB
求证:△ADC≌△CBA证明三角形全等时,要注意“隐含”条件:
如公共角,对顶角,公共边等。
, AD∥BC,准备条件指出范围列举条件得出结论你能说出证明三角形全等的一般步骤吗?证明:∵AD∥BC(已知)
∴∠1=∠2(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠1=∠2(已证)
AC=CA(公共边)
∴△ADC≌△CBA(SAS) 已知:AD=AC,若用SAS证两个三角形全等, 还需要添加一个什么条件?∠DAB=∠CAB 已知AC与BD交与O点,AO=CO,若用SAS证两个三角形全等, 还需要添加一个什么条件?BO=DO如果AB之间距离不容易直接测量,你有什么办法从图中得到AB之间的距离吗? 例2,如图,在湖泊的岸边有A,B两点,难以直接量出A,B两点间的距离.学习了边角边后,聪明的小杰说他会测量了.你知道他是怎么做的吗?为什么可以这样做?ABCA’B’解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A’,使A’C=AC;连接BC到点B’,使B’C=BC.连接A’B’,量出A’B’的长度.
由于△ABC≌△A’B’C’(SAS),所以AB=A’B’(全等三角形的对应边相等)因而,A’B’的长度就是A,B两点之间的距离. 应 用1.取点C2.找对应点A’和 B’3.连B,C1.学习了本节课以后,你有哪些收获?
2.你还有什么疑惑? 小 结 学习本节课后,我们知道已知两边及其夹角这三对元素对应相等,就可以判断两三角形全等,那么两个三角形具备其他三组元素对应相等,他们是否也能得到两个三角形全等呢? 思考课本95页,练习第1,2题 作 业谢谢! △ABC中,AB=4cm,AC=5cm,∠A=60°,试画出这个三角形。 活动三ABC4cm5cm60°△ABC就是所求图形
