2.2.3去括号
图片预览








文档简介
课件22张PPT。义务教育课程标准实验教科书
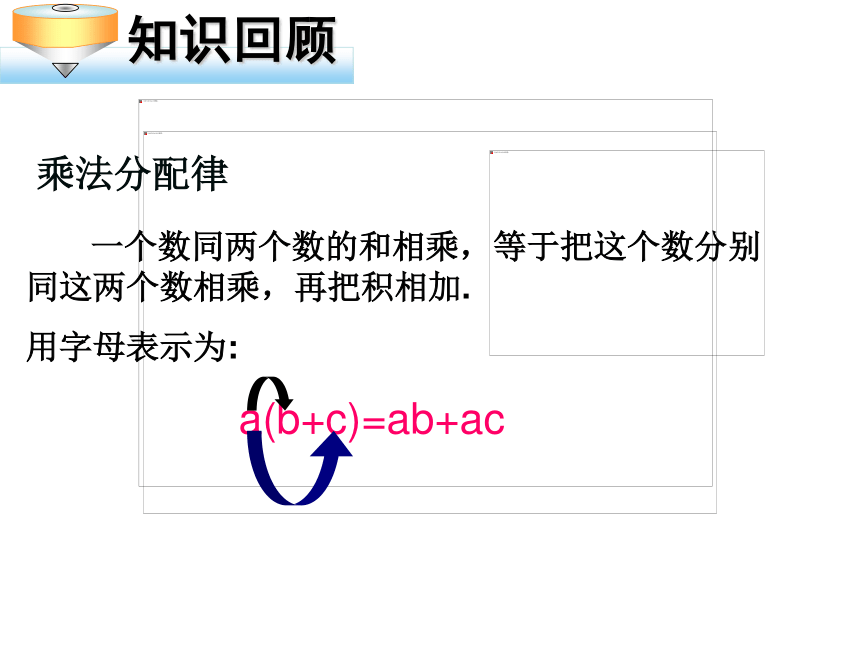
七年级上册第二章 整式的加减 人民教育出版社出版2.2 整式的加减(3) 一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
用字母表示为:
a(b+c)=ab+ac
乘法分配律利用乘法分配律计算:用类比方法计算下列各式:(1)2(χ+8)=
(2)-3(3χ+4)=
(3)- (7y-5)=
(4)+(-x+5)=
2χ+16-9χ-12-7y+5-x+5探求去括号法则: 去掉“+( )”,括号内各项的符号不变。
去掉“–( )”,括号内各项的符号改变。 用三个字母a、b、c表示去括号前后的变化规律: a+(b+c)
a-(b+c)= a+b+c
= a-b-c去括号法则去括号,看符号;
是正号,不变号;
是负号,都变号。 1.口答:去括号
(1) a + 2(– b + c ) =
( 2 ) ( a – b ) – ( c + d ) =
( 3 ) – (– a + b ) – c =
( 4 ) 2x– 3( x2 – y2 ) =
a-2b+2ca-b-c-da-b-c2x-3x2+3y21、去括号:
(1)2(1-3x)=___(4)-( )=_ _ (2)-3( =____(3)+7( )=_ _ 2.下列去括号正确吗?如有错误请改正。++-2 1.如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号相反。×××√你觉得我们去括号时,应该特别注意什么? 2.当括号前面有数字因数时,应用该数字因数乘以括号内的每一项,切勿漏乘。⑴⑵⑷⑶例1: 化简下列各式:利用去括号的规律进行整式的化简:⑴⑶⑵⑷化简下列各式例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时. (1) 2小时后两船相距多远? (2) 2小时后甲船比乙船多航行多少千米?分析: 由题意,我们知道:
顺水航速=船速+水速
逆水航速=船速-水速
而且,我们还知道路程等于航速乘以时间,所以两小时后两船的距离是:
甲船的路程+乙船的路程
两小时后,甲船比乙船多航行的路程
甲船的路程-乙船的路程
飞机的无风速度为a千米/时,风速为20千米/时,飞机顺风飞行4小时的行程是多少?飞机逆风飞行 3小时的行程是多少?两个行程相差多少?解:顺风速度=无风速度+风速= a+20(千米/时)
逆风速度=无风速度-风速= a-20(千米/时)∴顺风飞行4小时的行程为:
4(a+20) = 4a+80(千米) 逆风飞行3小时的行程为:
3(a-20) = 3a-60(千米)两个行程相差:
(4a+80)-(3a-60)= 4a+80-3a+60=a+140(千米)答:飞机顺风4小时飞行(4a+80)千米,逆风4小时飞行(3a-60)千米,两个行程相差(a+140)千米例3.
(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?例题解析2.判断下列计算是否正确:
不正确不正确
不正确正确3.下列去括号正确吗?如有错误 请改正。(1)-(-a-b)=a-b
(2)5x-(2x-1)-x2=5x-2x+1+x2
(3)3xy-0.5(xy-y2)=3xy-0.5xy+y2
(4)(a3+b3)-3(2a3-3b3)=a3+b3- 6a3+9b3×××√-先化简,再求值其中x = -3.(1) 4a-(a-3b)
a+(5a-3b)-2(a-2b)
3(2xy-y)-2(xy-y-1)-7
-5(1- x) 2.去括号,合并同类项例1 先去括号,再合并同类项:(1)(x+y-z)+(x-y+z)-(x-y-z)(2) 3(2x2-y2)-2(3y2-2x2)这节课我们学到了什么? 学习了类比的方法, 根据分配律来去括号,总结出了去括号的符号变化规律。作业:
课本第71页习题2.2第2题和第8题 如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号相反。祝同学们
天天向上,学习进步!
七年级上册第二章 整式的加减 人民教育出版社出版2.2 整式的加减(3) 一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
用字母表示为:
a(b+c)=ab+ac
乘法分配律利用乘法分配律计算:用类比方法计算下列各式:(1)2(χ+8)=
(2)-3(3χ+4)=
(3)- (7y-5)=
(4)+(-x+5)=
2χ+16-9χ-12-7y+5-x+5探求去括号法则: 去掉“+( )”,括号内各项的符号不变。
去掉“–( )”,括号内各项的符号改变。 用三个字母a、b、c表示去括号前后的变化规律: a+(b+c)
a-(b+c)= a+b+c
= a-b-c去括号法则去括号,看符号;
是正号,不变号;
是负号,都变号。 1.口答:去括号
(1) a + 2(– b + c ) =
( 2 ) ( a – b ) – ( c + d ) =
( 3 ) – (– a + b ) – c =
( 4 ) 2x– 3( x2 – y2 ) =
a-2b+2ca-b-c-da-b-c2x-3x2+3y21、去括号:
(1)2(1-3x)=___(4)-( )=_ _ (2)-3( =____(3)+7( )=_ _ 2.下列去括号正确吗?如有错误请改正。++-2 1.如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号相反。×××√你觉得我们去括号时,应该特别注意什么? 2.当括号前面有数字因数时,应用该数字因数乘以括号内的每一项,切勿漏乘。⑴⑵⑷⑶例1: 化简下列各式:利用去括号的规律进行整式的化简:⑴⑶⑵⑷化简下列各式例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时. (1) 2小时后两船相距多远? (2) 2小时后甲船比乙船多航行多少千米?分析: 由题意,我们知道:
顺水航速=船速+水速
逆水航速=船速-水速
而且,我们还知道路程等于航速乘以时间,所以两小时后两船的距离是:
甲船的路程+乙船的路程
两小时后,甲船比乙船多航行的路程
甲船的路程-乙船的路程
飞机的无风速度为a千米/时,风速为20千米/时,飞机顺风飞行4小时的行程是多少?飞机逆风飞行 3小时的行程是多少?两个行程相差多少?解:顺风速度=无风速度+风速= a+20(千米/时)
逆风速度=无风速度-风速= a-20(千米/时)∴顺风飞行4小时的行程为:
4(a+20) = 4a+80(千米) 逆风飞行3小时的行程为:
3(a-20) = 3a-60(千米)两个行程相差:
(4a+80)-(3a-60)= 4a+80-3a+60=a+140(千米)答:飞机顺风4小时飞行(4a+80)千米,逆风4小时飞行(3a-60)千米,两个行程相差(a+140)千米例3.
(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?例题解析2.判断下列计算是否正确:
不正确不正确
不正确正确3.下列去括号正确吗?如有错误 请改正。(1)-(-a-b)=a-b
(2)5x-(2x-1)-x2=5x-2x+1+x2
(3)3xy-0.5(xy-y2)=3xy-0.5xy+y2
(4)(a3+b3)-3(2a3-3b3)=a3+b3- 6a3+9b3×××√-先化简,再求值其中x = -3.(1) 4a-(a-3b)
a+(5a-3b)-2(a-2b)
3(2xy-y)-2(xy-y-1)-7
-5(1- x) 2.去括号,合并同类项例1 先去括号,再合并同类项:(1)(x+y-z)+(x-y+z)-(x-y-z)(2) 3(2x2-y2)-2(3y2-2x2)这节课我们学到了什么? 学习了类比的方法, 根据分配律来去括号,总结出了去括号的符号变化规律。作业:
课本第71页习题2.2第2题和第8题 如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号相反。祝同学们
天天向上,学习进步!
