平行四边形、矩形、菱形、正方形综合练习
文档属性
| 名称 | 平行四边形、矩形、菱形、正方形综合练习 |  | |
| 格式 | rar | ||
| 文件大小 | 54.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-18 17:45:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
平行四边形、矩形、菱形、正方形的练习 姓名
一、知识要点归纳:
1、平行四边形的概念、性质
①平行四边形两组对边分别平行; ②平行四边形的两组对边分别相等;
③平行四边形的两组对角分别相等,邻角互补; ④平行四边形的对角线互相平分。
2、平行四边形的判断方法:
(1)根据定义:两组对边分别平行的四边形叫做平行四边形.
(2)一组对边平行且相等的四边形是平行四边形。
(3) 两条对角线互相平分的四边形是平行四边形。
(4)两组对边分别相等的四边形是平行四边形。
注意:一组对边平行,一组对角相等的四边形是平行四边形;一组对边平行,另一组对边相等的四边形不一定是平行四边形,如:等腰梯形
3、矩形、菱形、正方形都是 的平行四边形,它们除了具有平行四边形的所有特征外,
还具有以下性质:矩形:四个角都是 、对角线 .
菱形:四条边都 、对角线互相 _________________________.
正方形:四条边都 、四个角 、对角线 .
2.矩形、菱形、正方形既是 图形,又是 对称图形;矩形、菱形、正
方形各有 对称轴,分别是 .它们的对称中心都是对角线
的 .
4、矩形判别方法有:
①有_______________________________________的四边形是矩形;
②有______________________________________的平行四边形是矩形;
③____________________________________________的平行四边形是矩形;
5、菱形判别方法有:
①有 的四边形是菱形;
②有 的平行四边形是菱形;
③ 的平行四边形是菱形;
6、正方形判别方法有:
① 的矩形是正方形;
② 的菱形是正方形.
二、经典例题
例1. 如图,平行四边形ABCD 的四个内角角平分线分别交于点E、F、G、H,
试判断四边形EFGH的形状,并说明理由。
例2.如图,菱形ABCD的对角线交于点O,E、F分别是OA、OC的中点,试判断四边形BEDF的形状,并说明理由。
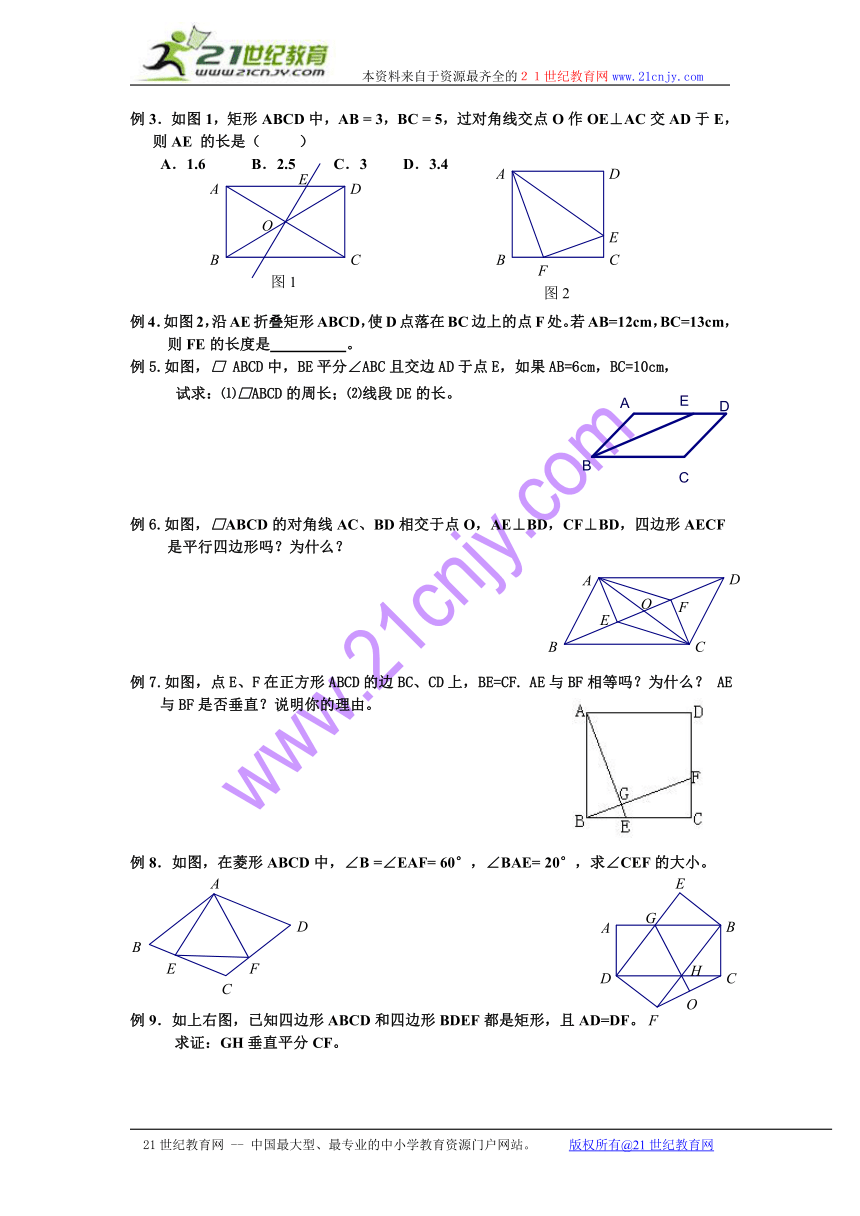
例3.如图1,矩形ABCD中,AB = 3,BC = 5,过对角线交点O作OE⊥AC交AD于E,则AE 的长是( )
A.1.6 B.2.5 C.3 D.3.4
例4.如图2,沿AE折叠矩形ABCD,使D点落在BC边上的点F处。若AB=12cm,BC=13cm,则FE的长度是 。
例5.如图,□ ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:⑴□ABCD的周长;⑵线段DE的长。
例6.如图,□ABCD的对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,四边形AECF是平行四边形吗?为什么?
例7.如图,点E、F在正方形ABCD的边BC、CD上,BE=CF. AE与BF相等吗?为什么? AE与BF是否垂直?说明你的理由。
例8.如图,在菱形ABCD中,∠B =∠EAF= 60°,∠BAE= 20°,求∠CEF的大小。
例9.如上右图,已知四边形ABCD和四边形BDEF都是矩形,且AD=DF。
求证:GH垂直平分CF。
三、作业与练习
1.如图1,矩形纸片ABCD中,AB=4,AD=3,折叠
纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
2.已知菱形的边长和一条对角线的长均为,则菱形的面积为( )
A. B. C. D.
3.下列条件中,能判定一个四边形为菱形的条件是( )
A、对角线互相平分的四边形 B、对角线互相垂直且平分的四边形
C、对角线相等的四边形 D、对角线相等且互相垂直的四边形
4.下列性质中,菱形具有而矩形不一定具有的性质是( )
A、对边平行且相等 B、对角线互相平分
C、内角和等于外角和 D、每一条对角线所在直线都是它的对称轴
5.如图2,矩形ABCD的两条对角线相交于点O,∠AOB= 60°,AB = 2,则矩形的对角线AC的长是( )
A.2 B.4 C. D.
6.如图3所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若
∠EFB=65°,则∠AED′ 等于 ( )
A.70° B.65° C.50° D.25°
7. 如图4,过四边形ABCD的顶点A、C、B、D分别作BD、AC的平行线围成四边形EFGH,如果EFGH成菱形,那么四边形ABCD必定是( )
A.菱形 B.平行四边形 C.矩形 D.对角线相等的四边形
8.点P是矩形ABCD内一点,且有PA = 3,PB = 4,PC = 5,则PD = 。
9.在矩形ABCD中,M是AD边的中点,N是DC边的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,那么∠MPA的度数是 ( )
A.33° B.66° C.45° D.78°
10.矩形的两条对角线所成的钝角是120°,若一条对角线的长为2,那么矩形的周长为( )
A、6 B、5.8 C、2(1+) D、5.2
11.已知矩形ABCD中,AB=3,BC=4,将矩形ABCD折叠,使C、A两点重合,则折痕EF的长为 。
12.已知菱形ABCD中,AC与BD相交O点,若∠BDC=,菱形的周长为20厘米,求菱形的面积.
13.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB = BF。
求证:四边形BNDM为菱形。
14.如图,平行四边形ABCD中,EF//BD,EF分别交AB,AD的延长线于E、F,交BC、CD于G、H,求证:EG=FH
15.如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.
16.如图1,在边长为5的正方形中,点、分别是、边上的点,且,
(1)如图2,延长交正方形外角平分线,试判断的大小关系,并说明理由;
(2)在图2的边上是否存在一点,使得四边形是平行四边形?若存在,请给予证明;若不存在,请说明理由.
图2
图1
图1
图3
图4
图2
图1
A
D
C
B
E
图2
B
C
E
D
A
F
P
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
平行四边形、矩形、菱形、正方形的练习 姓名
一、知识要点归纳:
1、平行四边形的概念、性质
①平行四边形两组对边分别平行; ②平行四边形的两组对边分别相等;
③平行四边形的两组对角分别相等,邻角互补; ④平行四边形的对角线互相平分。
2、平行四边形的判断方法:
(1)根据定义:两组对边分别平行的四边形叫做平行四边形.
(2)一组对边平行且相等的四边形是平行四边形。
(3) 两条对角线互相平分的四边形是平行四边形。
(4)两组对边分别相等的四边形是平行四边形。
注意:一组对边平行,一组对角相等的四边形是平行四边形;一组对边平行,另一组对边相等的四边形不一定是平行四边形,如:等腰梯形
3、矩形、菱形、正方形都是 的平行四边形,它们除了具有平行四边形的所有特征外,
还具有以下性质:矩形:四个角都是 、对角线 .
菱形:四条边都 、对角线互相 _________________________.
正方形:四条边都 、四个角 、对角线 .
2.矩形、菱形、正方形既是 图形,又是 对称图形;矩形、菱形、正
方形各有 对称轴,分别是 .它们的对称中心都是对角线
的 .
4、矩形判别方法有:
①有_______________________________________的四边形是矩形;
②有______________________________________的平行四边形是矩形;
③____________________________________________的平行四边形是矩形;
5、菱形判别方法有:
①有 的四边形是菱形;
②有 的平行四边形是菱形;
③ 的平行四边形是菱形;
6、正方形判别方法有:
① 的矩形是正方形;
② 的菱形是正方形.
二、经典例题
例1. 如图,平行四边形ABCD 的四个内角角平分线分别交于点E、F、G、H,
试判断四边形EFGH的形状,并说明理由。
例2.如图,菱形ABCD的对角线交于点O,E、F分别是OA、OC的中点,试判断四边形BEDF的形状,并说明理由。
例3.如图1,矩形ABCD中,AB = 3,BC = 5,过对角线交点O作OE⊥AC交AD于E,则AE 的长是( )
A.1.6 B.2.5 C.3 D.3.4
例4.如图2,沿AE折叠矩形ABCD,使D点落在BC边上的点F处。若AB=12cm,BC=13cm,则FE的长度是 。
例5.如图,□ ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:⑴□ABCD的周长;⑵线段DE的长。
例6.如图,□ABCD的对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,四边形AECF是平行四边形吗?为什么?
例7.如图,点E、F在正方形ABCD的边BC、CD上,BE=CF. AE与BF相等吗?为什么? AE与BF是否垂直?说明你的理由。
例8.如图,在菱形ABCD中,∠B =∠EAF= 60°,∠BAE= 20°,求∠CEF的大小。
例9.如上右图,已知四边形ABCD和四边形BDEF都是矩形,且AD=DF。
求证:GH垂直平分CF。
三、作业与练习
1.如图1,矩形纸片ABCD中,AB=4,AD=3,折叠
纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
2.已知菱形的边长和一条对角线的长均为,则菱形的面积为( )
A. B. C. D.
3.下列条件中,能判定一个四边形为菱形的条件是( )
A、对角线互相平分的四边形 B、对角线互相垂直且平分的四边形
C、对角线相等的四边形 D、对角线相等且互相垂直的四边形
4.下列性质中,菱形具有而矩形不一定具有的性质是( )
A、对边平行且相等 B、对角线互相平分
C、内角和等于外角和 D、每一条对角线所在直线都是它的对称轴
5.如图2,矩形ABCD的两条对角线相交于点O,∠AOB= 60°,AB = 2,则矩形的对角线AC的长是( )
A.2 B.4 C. D.
6.如图3所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若
∠EFB=65°,则∠AED′ 等于 ( )
A.70° B.65° C.50° D.25°
7. 如图4,过四边形ABCD的顶点A、C、B、D分别作BD、AC的平行线围成四边形EFGH,如果EFGH成菱形,那么四边形ABCD必定是( )
A.菱形 B.平行四边形 C.矩形 D.对角线相等的四边形
8.点P是矩形ABCD内一点,且有PA = 3,PB = 4,PC = 5,则PD = 。
9.在矩形ABCD中,M是AD边的中点,N是DC边的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,那么∠MPA的度数是 ( )
A.33° B.66° C.45° D.78°
10.矩形的两条对角线所成的钝角是120°,若一条对角线的长为2,那么矩形的周长为( )
A、6 B、5.8 C、2(1+) D、5.2
11.已知矩形ABCD中,AB=3,BC=4,将矩形ABCD折叠,使C、A两点重合,则折痕EF的长为 。
12.已知菱形ABCD中,AC与BD相交O点,若∠BDC=,菱形的周长为20厘米,求菱形的面积.
13.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB = BF。
求证:四边形BNDM为菱形。
14.如图,平行四边形ABCD中,EF//BD,EF分别交AB,AD的延长线于E、F,交BC、CD于G、H,求证:EG=FH
15.如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.
16.如图1,在边长为5的正方形中,点、分别是、边上的点,且,
(1)如图2,延长交正方形外角平分线,试判断的大小关系,并说明理由;
(2)在图2的边上是否存在一点,使得四边形是平行四边形?若存在,请给予证明;若不存在,请说明理由.
图2
图1
图1
图3
图4
图2
图1
A
D
C
B
E
图2
B
C
E
D
A
F
P
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
