14、1同底数幂的乘法与除法第二课时

课件24张PPT。西湖中学
芊芊十四章整式的乘法14、1同底数幂的乘法与除法
第二节1、an的意义是什么？a叫 ，n叫 。
2、同底数幂的乘法运算性质是什么？
3、计算：33×33= ， am·an= ，

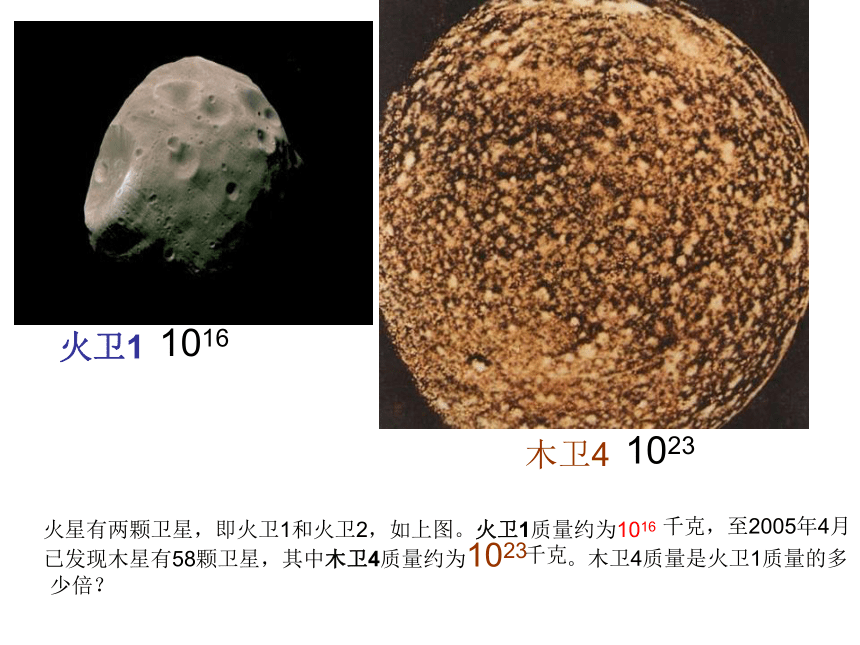
(a+b) 2· (a+b)3= ，一、复习火卫1木卫4火星有两颗卫星，即火卫1和火卫2，如上图。火卫1质量约为1016千克，至2005年4月
已发现木星有58颗卫星，其中木卫4质量约为1023千克。木卫4质量是火卫1质量的多少倍？10161023学习目标：知识与能力
掌握同底数幂的除法运算性质，能熟练准确地进行运算过程与方法
通过总结除法的运算法则和例题、习题的练习，培养和训练学生的抽象概括能力和综合解题计算能力情感、态度与价值观
在推导“法则”的过程中，发展推理能力和有条理的表达能力，渗透数学公式的简洁美与和谐美我们也可以用乘方的意义及分数的约分法则计算两个问题吗?2222222225-3(-3)5÷(-3)2=(-3)×(-3) × (-3)×(-3) ×(-3) =(-3)(3)(-3)×(-3)(2)=(-3)(5-2)
（1）1023÷1016=
（2）(–3)5÷(–3)2=
（3）( )6÷( )2=am–n107（-3）3
（ ）观察同底数幂相除，底数和指数的规律？
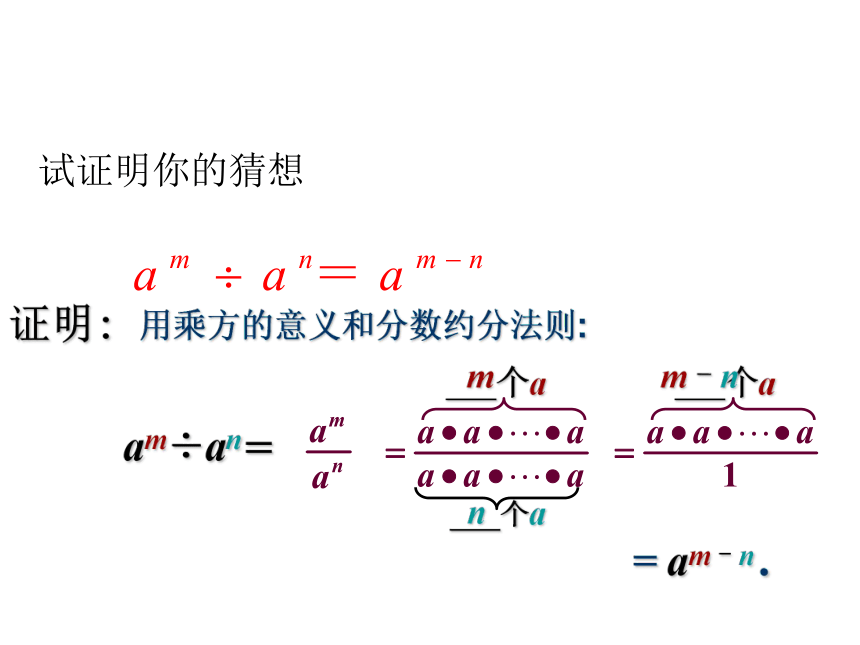
4证明: am÷an=mnm–n= am–n .试证明你的猜想 　　　 用乘方的意义和分数约分法则:同底数幂除法的性质即 am ÷ an = am-n
(a≠0，m、n为正整数，m>n)蓦然回首文字语言，
同底数幂相除，底数 ，指数
不变相减思考：同底数幂相除法则中各字母须满足什么条件 ？练习一判断
下面的计算对不对？如果不对，怎样改正？
（1）a6÷a2=a 3（ ） （2）(-a) 3÷(-a)2=a（ )）
（3）0.18÷0.16=0 .2( )（4）a3+a=a2( )
（5）c4÷c2=c6（ ） （6）c6÷( -c)2=-c4( )
× × (-a)3÷(-a)2=-a × 0.18÷0.16=0.12 =0.01 × a3+a × c4÷c2=c2× c6÷c2=c2 了不起！a6÷a2=a 4一起来找茬自学例4，口答P119页练习1、2题例4、计算：(-1.5)8÷(-1.5)7
注意：一个数可以看作这个数本身的一次方
相信你,你能行想一想am ÷ an ÷ ap 等于什么？ （a≠0,m,n,p是正整数，m＞m+p）例5、一个体重40千克的人体内约有血液3.1千克，其中约有红细胞250亿个。每克血液中约有多少个红细胞？注意：一亿=100000000=1×108例6、计算52m÷5m-1
变式训练，拓展延伸例8、计算(-x) 2÷x例7、计算（a+b）4÷(a+b)2
思考 已知：am=8,an=5. 求：
am-n的值解:am-n= am ÷ an= 8 ÷5 = 1.6拓展思维 公式逆应用
am-n=am÷an
(a≠0 ,m,n都是正整数，m＞n )
1、填空a13÷a( )=a7七、当堂达标 2、下列计算正确的是（ ）
A 、a6÷a3=a2 B、a3÷a2= 1
C 、(-a) 3÷(-a)=-a 2 D、(-m)3 ÷(-m)2=-m3、计算
（1）(-a)2÷a (2）(a-b)6÷(a-b)3· (a-b)
（3）an+4÷an-1 (n为正整数)（4）(-u)12÷(-u)6÷(-u)3 5、已知 ax=12,ay=3,则ax-y=6D=a=(a-b)4=a5=(-u)34畅谈收获同底数幂的除法性质：底数 ，指数 不变相减在利用同底数幂性质时应注意些什么？在利用同底数幂法则时应注意些什么？1.同底数幂相除的法则：注意a≠0,m,n都是正整数，且m>n.
2.幂的两个运算法则：3、运用法则的关键是看底数否相同，若底数不同，先化为同底数，后运用法则.而指数相减是指被除式的指数减去除式的指数,底数是多项式时，要把底数看做整体。指数是多项式时，应加上括号，再相减。
4、注意指数是1的情况5、多个同底数幂相乘除时，乘除混合运算的顺序与有理数混合运算顺序相同（即“从左到右”）应按顺序进行1.作业
P120页3、5题
B组1、3题
记住，别忘了我！敬请各位领导指导！谢谢！！谢谢各位同学的配合！！ 再见