【湘教版】高一(下)数学必修4同步辅导练习题四
文档属性
| 名称 | 【湘教版】高一(下)数学必修4同步辅导练习题四 |
|
|
| 格式 | zip | ||
| 文件大小 | 82.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-19 15:11:00 | ||
图片预览


文档简介
数学练习题四.
姓名______________
基础知识填空题:
可以由经过__________________;_______________;
_____________________三种变换而得到.如果它是由先向左平移,再将横坐标变为原来的而得到的,那么________.的单调递增区间是______________________;单调减区间是_________________.不等式的解集是________________.
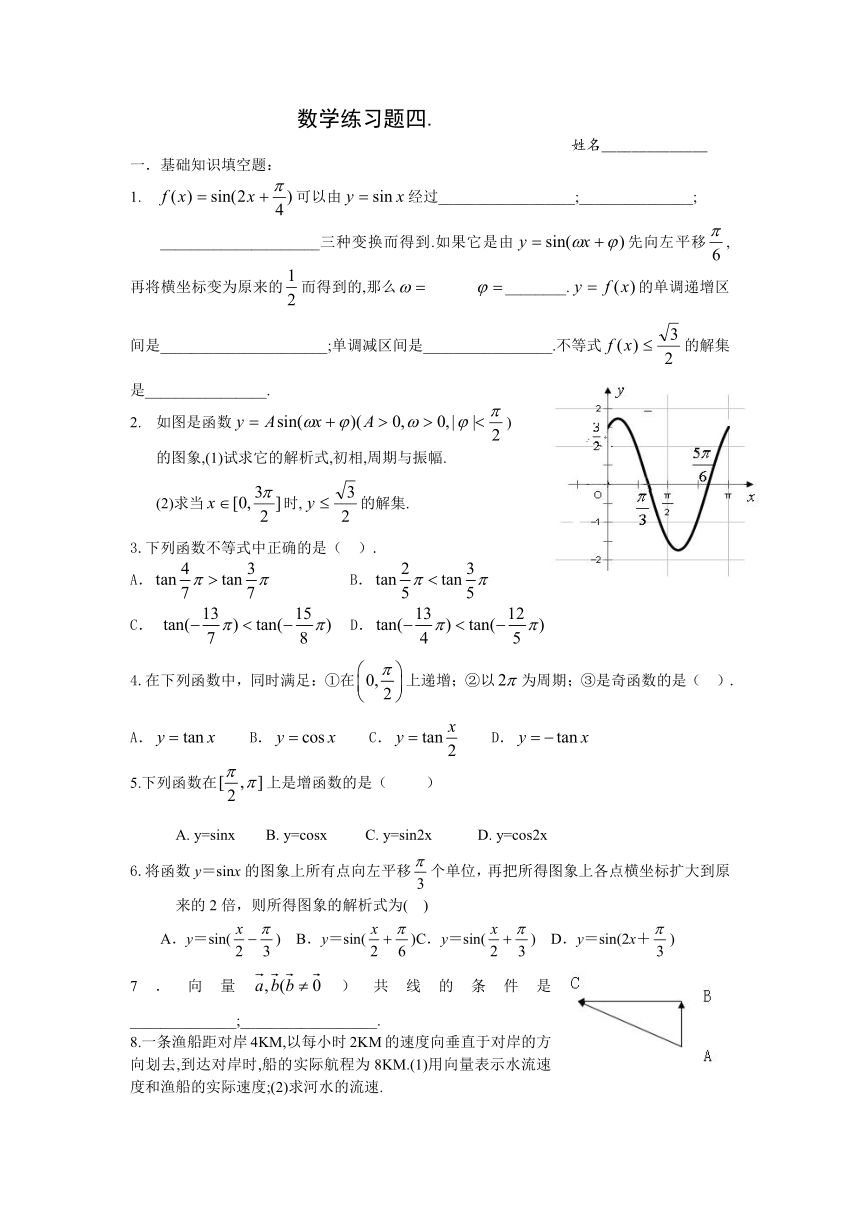
如图是函数)
的图象,(1)试求它的解析式,初相,周期与振幅.
(2)求当时,的解集.
3.下列函数不等式中正确的是( ).
A. B.
C. D.
4.在下列函数中,同时满足:①在上递增;②以为周期;③是奇函数的是( ).
A. B. C. D.
5.下列函数在上是增函数的是( )
A. y=sinx B. y=cosx C. y=sin2x D. y=cos2x
6.将函数y=sinx的图象上所有点向左平移个单位,再把所得图象上各点横坐标扩大到原来的2倍,则所得图象的解析式为( )
A.y=sin() B.y=sin()C.y=sin() D.y=sin(2x+)
7.向量)共线的条件是______________;__________________.
8.一条渔船距对岸4KM,以每小时2KM的速度向垂直于对岸的方向划去,到达对岸时,船的实际航程为8KM.(1)用向量表示水流速度和渔船的实际速度;(2)求河水的流速.
9.设平行四边形ABCD的对角线相交于点O,P为该平面内的任意一点,求证:
10.在平行四边形ABCD中,M、N分别是CD、BC的中点,设,试用为基底表示向量.
11.求满足的的集合.
12.已知向量=(6,2),=(-3,k),当k为何值时,有
(1),∥ (2),⊥ (3),与所成角θ是钝角 ?
练习题.
1.下列命题中为真命题的是 ( )
A.若则; B.若为非零向量,则;
C.若两个非零向量满足,则;
D.若两个非零向量满足则同向.
2.与向量平行的单位向量是 ( )
A. B.(- C.或 D.
3.已知A(,3),B(-2,-3),C(X,7),设且∥,则X的值是 ( )
A.0; B.3; C.15; D.18.
4.已知则与的夹角为 ( )
A. B. C. D.
5.点M是三角形ABC的重心,D,E,F分别是AB,BC,CA的中点,则
( )
A.6 B.-6 C. D.6
6.已知则的坐标是
7.已知=(1,2),=(x,1)且(+2)∥(2-),则x=_________.
8.已知A(3,4),B(12,7),点C在直线AB上,且则点
C的坐标为 .
9.函数y=sin2x的单调减区间是( )
A. B.
C. D.
10.函数 y=sin 的单调增区间是( ).
A. B.
C. D.
11.已知角的终边上一点P(- ,m),且sinθ= eq \f(,4)m,求cosθ与tanθ的值.
12、要得到函数的图象,只需将函数的图象 ( )
A. 向左平移 B. 向右平移 C. 向左平移 D. 向右平移
13、某函数的图象向右平移后得到的图象的函数式是,则此函数表达式是( )
A. B. C. D.
14、同时具有性质“(1)最小正周期是;(2)图像关于直线对称;(3)在上是增函数”的一个函数是( )
A. B. C. D.
15.函数f(x)=5sin(2x+ )的图象关于y轴对称, 应满足的条件是________.
16.在五边形ABCDE中,若四边形ACDE是平行四边形,且试用,表示向量及.
17,设且在的延长线上,使,,则求点
的坐标
18.(本小题满分12分)
已知函数,。
(I)当函数取得最大值时,求自变量的集合;
(2)若,求函数的单调递增区间。
19.已知向量a、b、c两两所成的角相等,并且,,,
求向量a+b+c的长度;
20,已知向量=(3, -4), =(6, -3),=(5-m, -3-m),
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
解:(1)已知向量
若点A、B、C能构成三角形,则这三点不共线, 3分
故知.
∴实数时,满足的条件. 5分
(2)若△ABC为直角三角形,且∠A为直角,则, 7分
∴,解得. 10分
姓名______________
基础知识填空题:
可以由经过__________________;_______________;
_____________________三种变换而得到.如果它是由先向左平移,再将横坐标变为原来的而得到的,那么________.的单调递增区间是______________________;单调减区间是_________________.不等式的解集是________________.
如图是函数)
的图象,(1)试求它的解析式,初相,周期与振幅.
(2)求当时,的解集.
3.下列函数不等式中正确的是( ).
A. B.
C. D.
4.在下列函数中,同时满足:①在上递增;②以为周期;③是奇函数的是( ).
A. B. C. D.
5.下列函数在上是增函数的是( )
A. y=sinx B. y=cosx C. y=sin2x D. y=cos2x
6.将函数y=sinx的图象上所有点向左平移个单位,再把所得图象上各点横坐标扩大到原来的2倍,则所得图象的解析式为( )
A.y=sin() B.y=sin()C.y=sin() D.y=sin(2x+)
7.向量)共线的条件是______________;__________________.
8.一条渔船距对岸4KM,以每小时2KM的速度向垂直于对岸的方向划去,到达对岸时,船的实际航程为8KM.(1)用向量表示水流速度和渔船的实际速度;(2)求河水的流速.
9.设平行四边形ABCD的对角线相交于点O,P为该平面内的任意一点,求证:
10.在平行四边形ABCD中,M、N分别是CD、BC的中点,设,试用为基底表示向量.
11.求满足的的集合.
12.已知向量=(6,2),=(-3,k),当k为何值时,有
(1),∥ (2),⊥ (3),与所成角θ是钝角 ?
练习题.
1.下列命题中为真命题的是 ( )
A.若则; B.若为非零向量,则;
C.若两个非零向量满足,则;
D.若两个非零向量满足则同向.
2.与向量平行的单位向量是 ( )
A. B.(- C.或 D.
3.已知A(,3),B(-2,-3),C(X,7),设且∥,则X的值是 ( )
A.0; B.3; C.15; D.18.
4.已知则与的夹角为 ( )
A. B. C. D.
5.点M是三角形ABC的重心,D,E,F分别是AB,BC,CA的中点,则
( )
A.6 B.-6 C. D.6
6.已知则的坐标是
7.已知=(1,2),=(x,1)且(+2)∥(2-),则x=_________.
8.已知A(3,4),B(12,7),点C在直线AB上,且则点
C的坐标为 .
9.函数y=sin2x的单调减区间是( )
A. B.
C. D.
10.函数 y=sin 的单调增区间是( ).
A. B.
C. D.
11.已知角的终边上一点P(- ,m),且sinθ= eq \f(,4)m,求cosθ与tanθ的值.
12、要得到函数的图象,只需将函数的图象 ( )
A. 向左平移 B. 向右平移 C. 向左平移 D. 向右平移
13、某函数的图象向右平移后得到的图象的函数式是,则此函数表达式是( )
A. B. C. D.
14、同时具有性质“(1)最小正周期是;(2)图像关于直线对称;(3)在上是增函数”的一个函数是( )
A. B. C. D.
15.函数f(x)=5sin(2x+ )的图象关于y轴对称, 应满足的条件是________.
16.在五边形ABCDE中,若四边形ACDE是平行四边形,且试用,表示向量及.
17,设且在的延长线上,使,,则求点
的坐标
18.(本小题满分12分)
已知函数,。
(I)当函数取得最大值时,求自变量的集合;
(2)若,求函数的单调递增区间。
19.已知向量a、b、c两两所成的角相等,并且,,,
求向量a+b+c的长度;
20,已知向量=(3, -4), =(6, -3),=(5-m, -3-m),
(1)若点A、B、C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
解:(1)已知向量
若点A、B、C能构成三角形,则这三点不共线, 3分
故知.
∴实数时,满足的条件. 5分
(2)若△ABC为直角三角形,且∠A为直角,则, 7分
∴,解得. 10分
