【湘教版】高一(下)数学必修4同步辅导练习题八
文档属性
| 名称 | 【湘教版】高一(下)数学必修4同步辅导练习题八 |
|
|
| 格式 | zip | ||
| 文件大小 | 123.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-19 15:11:00 | ||
图片预览




文档简介
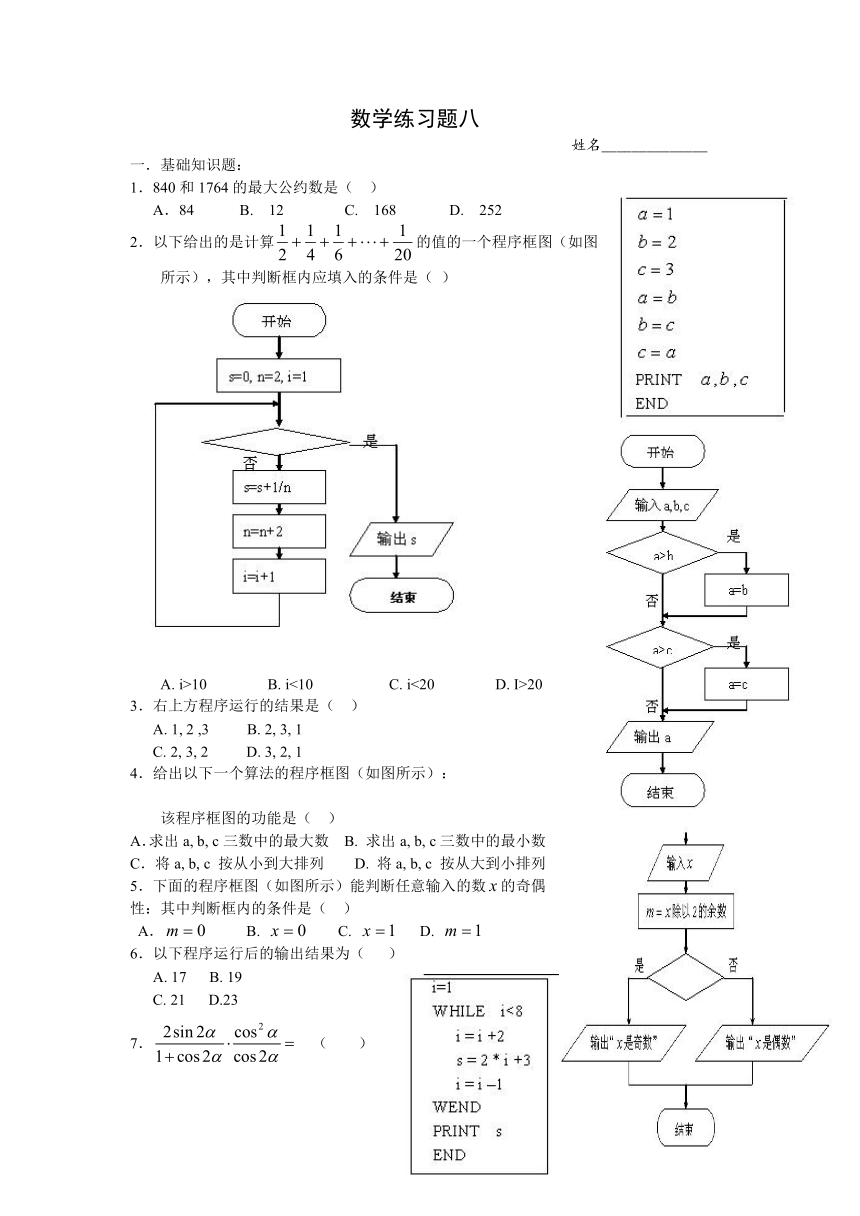
数学练习题八
姓名______________
基础知识题:
1.840和1764的最大公约数是( )
A.84 B. 12 C. 168 D. 252
2.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是( )
A. i>10 B. i<10 C. i<20 D. I>20
3.右上方程序运行的结果是( )
A. 1, 2 ,3 B. 2, 3, 1
C. 2, 3, 2 D. 3, 2, 1
4.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
5.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:其中判断框内的条件是( )
A. B. C. D.
6.以下程序运行后的输出结果为( )
A. 17 B. 19
C. 21 D.23
7. ( )
A. B. C. 1 D.
8.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是 ( )
A.2π B.π C. D.
9. 若,且为第三象限角,则的值为( )
A. B. C. D.
10. 若将函数的图像向左平移个单位后得到的图像的函数解析式为
A. B.
C. D.
11.当时,函数的最小值为 ( )
A. B. C.5 D.
12.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是( )
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
二、填空题(本大题共4小题,每小题4分,共16分)
13.三个数72,120,168的最大公约数是_______。
14.若输入8,则下列程序执行后输出的结果是________。
15.将二进制数化为十进制数,结果为__________
已知:八进制数则A=________;B=________.
已知:八进制数则A+B+C+D=_________.
16.=
17. 已知, ⑴求的值;⑵求的值
18.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
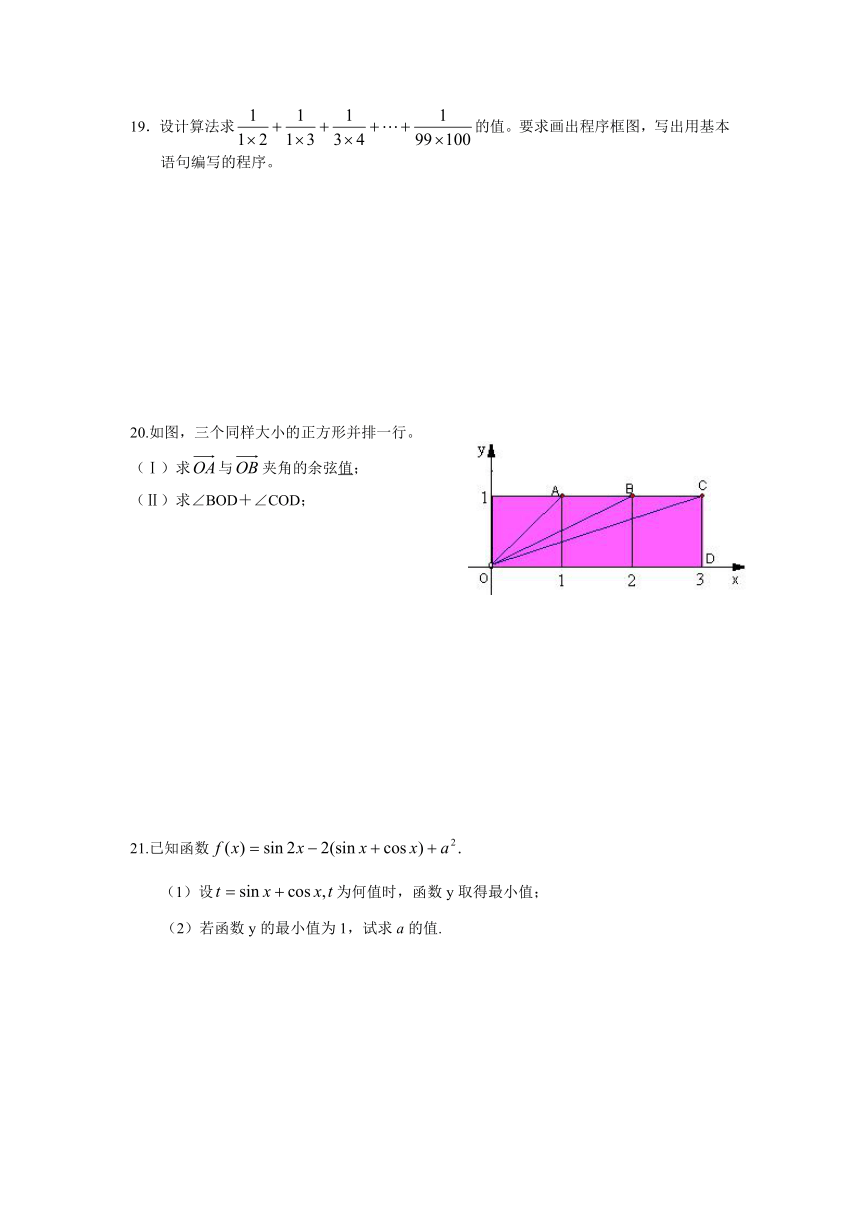
19.设计算法求的值。要求画出程序框图,写出用基本语句编写的程序。
20.如图,三个同样大小的正方形并排一行。
(Ⅰ)求与夹角的余弦值;
(Ⅱ)求∠BOD+∠COD;
21.已知函数
(1)设为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.
二.检测题:
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
2.右侧程序执行后输出的结果是( )
A. –1 B. 0 C. 1 D. 2
3.在锐角△ABC中,设则x,y的大小关系为( )
(A) (B) (C) (D)
4.已知对任意,不等式恒成立,则实数的取值范围是_________________
5.已知点A(2,-4),B(-6,2),则AB的中点M的坐标为 _______ ;
6.若与共线,则= ;
7.若,则= ;
8.函数的值域是 ;
9.将函数图象上每一个点的横坐标扩大为原来的2倍,所得图象所对应的函数解析式为 ;若将的图象沿轴向左平移个单位(),所得函数的图象关于轴对称,则的最小值为 .
10.已知x,y都是实数,且,则的值为_________
11、给出下列命题:(1)函数是偶函数
(2)是函数的一条对称轴方程
(3)若是第一象限的角,且,则
(4)在中,若,则;反之若,则
其中正确命题的序号是________________________________
12.用秦九韶算法计算多项式 当时的值为 _________。
13.某市电信部门规定:拔打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话时间以分钟计,不足1分钟时按1分钟计),试设计一个计算通话费的算法。要求写出算法,画出程序框图,编写程序。
14.(本小题10分)已知函数。
(Ⅰ)求的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出在一个周期内的图象。
(Ⅲ)写出函数的递减区间。
15.已知,,且,,求的值。
16.已知是关于X的方程的两个实根,,求的值。
数学练习题八答案
姓名______________
基础知识题:
1.840和1764的最大公约数是(A )
A.84 B. 12 C. 168 D. 252
2.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是(A)
A. i>10 B. i<10 C. i<20 D. I>20
3.右上方程序运行的结果是( C)
A. 1, 2 ,3 B. 2, 3, 1
C. 2, 3, 2 D. 3, 2, 1
4.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( B )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
5.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:其中判断框内的条件是( D )
A. B. C. D.
6.以下程序运行后的输出结果为( C )
A. 17 B. 19
C. 21 D.23
7. ( B )
A. B. C. 1 D.
8.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是 ( B )
A.2π B.π C. D.
9. 若,且为第三象限角,则的值为( D )
A. B. C. D.
10. 若将函数的图像向左平移个单位后得到的图像的函数解析式为D
A. B.
C. D.
11.当时,函数的最小值为 ( C )
A. B. C.5 D.
12.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是(A)
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
二、填空题(本大题共4小题,每小题4分,共16分)
13.三个数72,120,168的最大公约数是_______。24
14.若输入8,则下列程序执行后输出的结果是________。0.7
15.将二进制数化为十进制数,结果为__________ 45,
已知:八进制数则A=___7_____;B=__6______.
已知:八进制数则A+B+C+D=__11,13,14,16__,
16.= -1
17. 已知, ⑴求的值;⑵求的值
18.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
18.(1)用辗转相除法求840与1764的最大公约数。
1764=8402+84,840=8410+0,所以840与1764的最大公约数就是84。
(2)用更相减损术求440与556的最大公约数。
556-440=116,440-116=324,324-116=208,208-116=92,116-92=24,92-24=68,
68-24=44,44-24=20,24-20=4,20-4=16,16-4=12,12-4=8,8-4=4。
440与556的最大公约数是4。
19.设计算法求的值。要求画出程序框图,写出用基本语句编写的程序。
这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法。程序框图如图所示:
20.如图,三个同样大小的正方形并排一行。
(Ⅰ)求与夹角的余弦值;
(Ⅱ)求∠BOD+∠COD;
解:(Ⅰ)因为A(1,1),B(2,1)
所以=(1,1),=(2,1)……(2分)
cos∠AOB=. ……(4分)
(Ⅱ)因为C(3,1),D(3,0),所以tan∠BOD=,tan∠COD= ……(6分)
所以 tan(∠BOD+∠COD)= ……(8分)
又因为∠BOD和∠COD均为锐角,故∠BOD+∠COD=45° ……(10分)
考查向量数量积的几何意义,向量夹角求法,两角和的正切,。中等题。
21.已知函数
(1)设为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.
二.检测题:
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( D )
一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
2.右侧程序执行后输出的结果是(B )
A. –1 B. 0 C. 1 D. 2
3.在锐角△ABC中,设则x,y的大小关系为( B )
(A) (B) (C) (D)
4.已知对任意,不等式恒成立,则实数的取值范围是
5.已知点A(2,-4),B(-6,2),则AB的中点M的坐标为 (-2,-1) ;
考查中点坐标公式,简单题。
6.若与共线,则= -6 ;
考查共线向量,简单题。
7.若,则= -3 /4 ;
8.函数的值域是 [-1,3] ;
9.将函数图象上每一个点的横坐标扩大为原来的2倍,所得图象所对应的函数解析式为 ;若将的图象沿轴向左平移个单位(),所得函数的图象关于轴对称,则的最小值为 .
10.已知x,y都是实数,且,则的值为_________。0
11、给出下列命题:(1)函数是偶函数
(2)是函数的一条对称轴方程
(3)若是第一象限的角,且,则
(4)在中,若,则;反之若,则
其中正确命题的序号是________________________________(1)(2)(4)
12.用秦九韶算法计算多项式 当时的值为 _________。 0
13.某市电信部门规定:拔打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话时间以分钟计,不足1分钟时按1分钟计),试设计一个计算通话费的算法。要求写出算法,画出程序框图,编写程序。
解:我们用(单位:元)表示通话费用,(单位:分钟)表示通话时间,则依题意必有
算法步骤如下:
第一步:输入通话时间;第二步:如果,那么;否则令;
第三步:输出通话费用。
程序框图如下所示:
程序为:
考查向量的平行与垂直、向量的坐标运算,简单题。
14.(本小题10分)已知函数。
(Ⅰ)求的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出在一个周期内的图象。
(Ⅲ)写出函数的递减区间。
解:(Ⅰ)==
0 2 0 -2 0
函数的周期为T=,
振幅为2。
(Ⅱ)列表:
图象如上(作图不规范者扣1分)。
(Ⅲ)由解得:
所以函数的递减区间为 ……(10分)
考查两角和与差的三角函数及函数的图象及性质。中等题。
15.已知,,且,,求的值。
18.
16.已知是关于X的方程的两个实根,,求的值。
19.. ,,此时
姓名______________
基础知识题:
1.840和1764的最大公约数是( )
A.84 B. 12 C. 168 D. 252
2.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是( )
A. i>10 B. i<10 C. i<20 D. I>20
3.右上方程序运行的结果是( )
A. 1, 2 ,3 B. 2, 3, 1
C. 2, 3, 2 D. 3, 2, 1
4.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
5.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:其中判断框内的条件是( )
A. B. C. D.
6.以下程序运行后的输出结果为( )
A. 17 B. 19
C. 21 D.23
7. ( )
A. B. C. 1 D.
8.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是 ( )
A.2π B.π C. D.
9. 若,且为第三象限角,则的值为( )
A. B. C. D.
10. 若将函数的图像向左平移个单位后得到的图像的函数解析式为
A. B.
C. D.
11.当时,函数的最小值为 ( )
A. B. C.5 D.
12.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是( )
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
二、填空题(本大题共4小题,每小题4分,共16分)
13.三个数72,120,168的最大公约数是_______。
14.若输入8,则下列程序执行后输出的结果是________。
15.将二进制数化为十进制数,结果为__________
已知:八进制数则A=________;B=________.
已知:八进制数则A+B+C+D=_________.
16.=
17. 已知, ⑴求的值;⑵求的值
18.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
19.设计算法求的值。要求画出程序框图,写出用基本语句编写的程序。
20.如图,三个同样大小的正方形并排一行。
(Ⅰ)求与夹角的余弦值;
(Ⅱ)求∠BOD+∠COD;
21.已知函数
(1)设为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.
二.检测题:
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
2.右侧程序执行后输出的结果是( )
A. –1 B. 0 C. 1 D. 2
3.在锐角△ABC中,设则x,y的大小关系为( )
(A) (B) (C) (D)
4.已知对任意,不等式恒成立,则实数的取值范围是_________________
5.已知点A(2,-4),B(-6,2),则AB的中点M的坐标为 _______ ;
6.若与共线,则= ;
7.若,则= ;
8.函数的值域是 ;
9.将函数图象上每一个点的横坐标扩大为原来的2倍,所得图象所对应的函数解析式为 ;若将的图象沿轴向左平移个单位(),所得函数的图象关于轴对称,则的最小值为 .
10.已知x,y都是实数,且,则的值为_________
11、给出下列命题:(1)函数是偶函数
(2)是函数的一条对称轴方程
(3)若是第一象限的角,且,则
(4)在中,若,则;反之若,则
其中正确命题的序号是________________________________
12.用秦九韶算法计算多项式 当时的值为 _________。
13.某市电信部门规定:拔打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话时间以分钟计,不足1分钟时按1分钟计),试设计一个计算通话费的算法。要求写出算法,画出程序框图,编写程序。
14.(本小题10分)已知函数。
(Ⅰ)求的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出在一个周期内的图象。
(Ⅲ)写出函数的递减区间。
15.已知,,且,,求的值。
16.已知是关于X的方程的两个实根,,求的值。
数学练习题八答案
姓名______________
基础知识题:
1.840和1764的最大公约数是(A )
A.84 B. 12 C. 168 D. 252
2.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是(A)
A. i>10 B. i<10 C. i<20 D. I>20
3.右上方程序运行的结果是( C)
A. 1, 2 ,3 B. 2, 3, 1
C. 2, 3, 2 D. 3, 2, 1
4.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( B )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
5.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:其中判断框内的条件是( D )
A. B. C. D.
6.以下程序运行后的输出结果为( C )
A. 17 B. 19
C. 21 D.23
7. ( B )
A. B. C. 1 D.
8.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则的最小正周期是 ( B )
A.2π B.π C. D.
9. 若,且为第三象限角,则的值为( D )
A. B. C. D.
10. 若将函数的图像向左平移个单位后得到的图像的函数解析式为D
A. B.
C. D.
11.当时,函数的最小值为 ( C )
A. B. C.5 D.
12.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是(A)
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
二、填空题(本大题共4小题,每小题4分,共16分)
13.三个数72,120,168的最大公约数是_______。24
14.若输入8,则下列程序执行后输出的结果是________。0.7
15.将二进制数化为十进制数,结果为__________ 45,
已知:八进制数则A=___7_____;B=__6______.
已知:八进制数则A+B+C+D=__11,13,14,16__,
16.= -1
17. 已知, ⑴求的值;⑵求的值
18.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
18.(1)用辗转相除法求840与1764的最大公约数。
1764=8402+84,840=8410+0,所以840与1764的最大公约数就是84。
(2)用更相减损术求440与556的最大公约数。
556-440=116,440-116=324,324-116=208,208-116=92,116-92=24,92-24=68,
68-24=44,44-24=20,24-20=4,20-4=16,16-4=12,12-4=8,8-4=4。
440与556的最大公约数是4。
19.设计算法求的值。要求画出程序框图,写出用基本语句编写的程序。
这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法。程序框图如图所示:
20.如图,三个同样大小的正方形并排一行。
(Ⅰ)求与夹角的余弦值;
(Ⅱ)求∠BOD+∠COD;
解:(Ⅰ)因为A(1,1),B(2,1)
所以=(1,1),=(2,1)……(2分)
cos∠AOB=. ……(4分)
(Ⅱ)因为C(3,1),D(3,0),所以tan∠BOD=,tan∠COD= ……(6分)
所以 tan(∠BOD+∠COD)= ……(8分)
又因为∠BOD和∠COD均为锐角,故∠BOD+∠COD=45° ……(10分)
考查向量数量积的几何意义,向量夹角求法,两角和的正切,。中等题。
21.已知函数
(1)设为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.
二.检测题:
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( D )
一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
2.右侧程序执行后输出的结果是(B )
A. –1 B. 0 C. 1 D. 2
3.在锐角△ABC中,设则x,y的大小关系为( B )
(A) (B) (C) (D)
4.已知对任意,不等式恒成立,则实数的取值范围是
5.已知点A(2,-4),B(-6,2),则AB的中点M的坐标为 (-2,-1) ;
考查中点坐标公式,简单题。
6.若与共线,则= -6 ;
考查共线向量,简单题。
7.若,则= -3 /4 ;
8.函数的值域是 [-1,3] ;
9.将函数图象上每一个点的横坐标扩大为原来的2倍,所得图象所对应的函数解析式为 ;若将的图象沿轴向左平移个单位(),所得函数的图象关于轴对称,则的最小值为 .
10.已知x,y都是实数,且,则的值为_________。0
11、给出下列命题:(1)函数是偶函数
(2)是函数的一条对称轴方程
(3)若是第一象限的角,且,则
(4)在中,若,则;反之若,则
其中正确命题的序号是________________________________(1)(2)(4)
12.用秦九韶算法计算多项式 当时的值为 _________。 0
13.某市电信部门规定:拔打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话时间以分钟计,不足1分钟时按1分钟计),试设计一个计算通话费的算法。要求写出算法,画出程序框图,编写程序。
解:我们用(单位:元)表示通话费用,(单位:分钟)表示通话时间,则依题意必有
算法步骤如下:
第一步:输入通话时间;第二步:如果,那么;否则令;
第三步:输出通话费用。
程序框图如下所示:
程序为:
考查向量的平行与垂直、向量的坐标运算,简单题。
14.(本小题10分)已知函数。
(Ⅰ)求的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出在一个周期内的图象。
(Ⅲ)写出函数的递减区间。
解:(Ⅰ)==
0 2 0 -2 0
函数的周期为T=,
振幅为2。
(Ⅱ)列表:
图象如上(作图不规范者扣1分)。
(Ⅲ)由解得:
所以函数的递减区间为 ……(10分)
考查两角和与差的三角函数及函数的图象及性质。中等题。
15.已知,,且,,求的值。
18.
16.已知是关于X的方程的两个实根,,求的值。
19.. ,,此时
