【湘教版】高一(下)数学必修4同步辅导练习题十一
文档属性
| 名称 | 【湘教版】高一(下)数学必修4同步辅导练习题十一 |

|
|
| 格式 | zip | ||
| 文件大小 | 184.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-19 15:11:00 | ||
图片预览




文档简介
综合练习题十一
姓名_______________
一.基础知识练习题
1. 在抽取产品的尺寸过程中,将其尺寸分成若干组,是其中一组,抽查出的个体在该组上的频率为m ,该组上的直方图的高为h,则 ( )
A.hm B. C. D.h+m
2..现有辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,
时速在的汽车大约有( )
.辆 .辆 .辆 .80辆
3.已知,若0≤θ≤π,
使函数f(x)为偶函数的θ为 ( )
(A) (B) (C) (D)
4.某题的得分情况如下:其中众数是 ( )
得分/分 0 1 2 3 4
百分率/(%) 37.0 8.6 6.0 28.2 20.2
(A)37.0% (B)20.2% (C)0分 (D)4分
5.已知若则点的坐标为( )
6.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
再将所得的图象向左平移个单位,得到的图象对应的解析式是( )
A. B.
C. D.
7.. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是( )
A. B. C. D.
8. 在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是. ( )
A. B. C. D.
9. 一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )
A. B. C. D.
10.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是 ( )
(A) (B) (C) (D)
11. 6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A B. C. D.
12.有所有的两位数(10~99)中任取一个数,则这个数能被2或3整除的概率是( )
A. B. C. D.
13.(2009辽宁卷理)某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 h.
14.有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图
频率/组距
15.从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
16..将二进制数1010 101(2) 化为十进制结果为 ;
再将该数化为八进制数,结果为 .
17.将一颗骰子先后抛掷2次,观察向上的点数以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率为_____
19.(2009年广东卷文) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
20. 已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
21.购物广场拟在五一节举行抽奖活动,规则是:从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;
(2)求中奖的概率。
22.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.
(1)求事件“”的概率;
(2)求事件“”的概率.
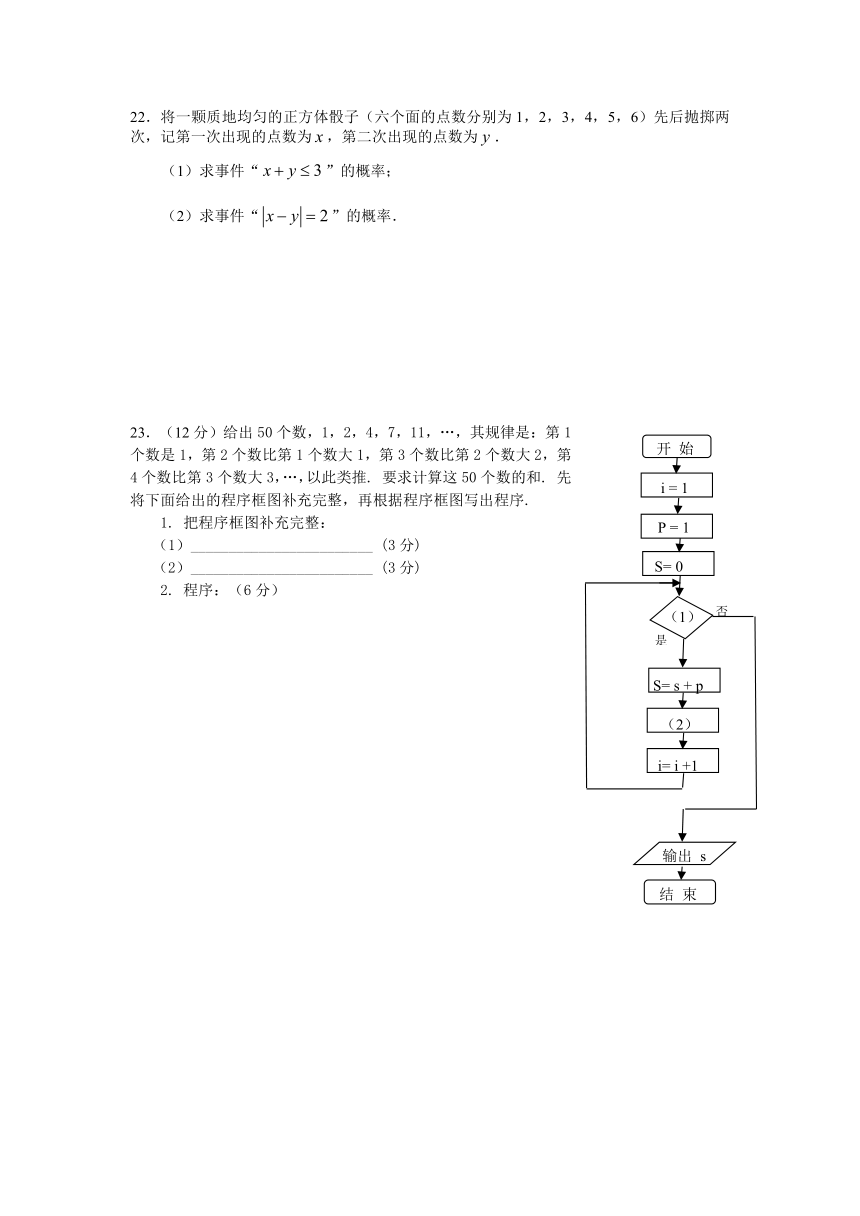
23.(12分)给出50个数,1,2,4,7,11,…,其规律是:第1
个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第
4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先
将下面给出的程序框图补充完整,再根据程序框图写出程序.
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (3分)
2. 程序:(6分)
二.练习题。
1.一个容量为20的样本数据,分组与各组内频数如下:(10,20),2;(20, 30),3;(30,40),4;(40,50),5;(50,60),4;(60,70],2.则样本在(10,50]上的频率为 ( )
(A)90% (B)50% (C) 70% (D)25%
2.已知,,则( )
A. B. C. D.
3.已知平面向量,,且,则( )
A. B. C. D.
4.函数的最小值为( )
A. B. C. D.
5.若( )
A. B. C. D.
6. 已知右图是函数的图象,那么( )
A. B.
C. D.
7.已知,,则 .
8.若=,=,则在上的投影为________________。
9.函数的单调递减区间是______________.
10.(12分)设计一个算法求:;试用流程图和相应程序表示.
11.将一枚骰子抛掷两次,若先后出现的点数分别为,则方程有实根的概率为( )
A B C D
12.(本小题满分14分)函数在同一个周期内,当 时取最大值1,当时,取最小值.
(1)求函数的解析式
(2)函数的图象经过怎样的变换可得到的图象?
(3)若函数满足方程求在内的所有实数根之和.
综合练习题十一答案
一.基础知识练习题
1. 在抽取产品的尺寸过程中,将其尺寸分成若干组,是其中一组,抽查出的个体在该组上的频率为m ,该组上的直方图的高为h,则 ( B )
A.hm B. C. D.h+m
2..现有辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,
时速在的汽车大约有( C )
.辆 .辆 .辆 .80辆
3.已知,若0≤θ≤π,
使函数f(x)为偶函数的θ为
(A) (B) (C) (D)
4.某题的得分情况如下:其中众数是 ( C )
得分/分 0 1 2 3 4
百分率/(%) 37.0 8.6 6.0 28.2 20.2
(A)37.0% (B)20.2% (C)0分 (D)4分
5.已知若则点的坐标为(C )
6.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
再将所得的图象向左平移个单位,得到的图象对应的解析式是( C )
A. B.
C. D.
7.. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是(A)
A. B. C. D.
8. 在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是.
A. B. C. D.
9. 一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )
A. B. C. D.
10.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是 ( )
(A) (B) (C) (D)
11. 6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A B. C. D.
12.有所有的两位数(10~99)中任取一个数,则这个数能被2或3整除的概率是( )
A. B. C. D.
13.(2009辽宁卷理)某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 h. 1013
14.有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图
解:(1)样本的频率分布表:
分组 频数 频率 频率∕组距
6 0.06 0.02
16 0.16 0.053
18 0.18 0.06
22 0.22 0.073
20 0.20 0.067
10 0.10 0.033
8 0.08 0.027
(2)频率分布直方图
频率/组距
0.073
0.020
12.5 15.5 18.5 21.5 24.5 27.5 30.5 33.5
频率折线图略
15.从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
16..将二进制数1010 101(2) 化为十进制结果为 85 ;
再将该数化为八进制数,结果为 . 125(8)
17.将一颗骰子先后抛掷2次,观察向上的点数以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率为_____
18. 10产品中有4件次品,从中任意取出2件,在所取得的产品中发现一件次品,则另一件也是次品的概率为___________
19.(2009年广东卷文) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
【解析】(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
20. 已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
解:记“甲射击一次,命中7环以下”为事件,“甲射击一次,命中7环”为事件,由于在一次射击中,与不可能同时发生,故与是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为,
由互斥事件的概率加法公式,.
答:甲射击一次,命中不足8环的概率是0.22.…………………………………6分
(2)方法1:记“甲射击一次,命中8环”为事件,“甲射击一次,命中9环(含9环)以上”为事件,则“甲射击一次,至少命中7环”的事件为,
∴.
答:甲射击一次,至少命中7环的概率为0.9.…………………………………12分
方法2:∵“甲射击一次,至少命中7环”为事件,
∴=1-0.1=0.9.
答:甲射击一次,至少命中7环的概率为0.9.………
21.购物广场拟在五一节举行抽奖活动,规则是:从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;
(2)求中奖的概率。
解:两个小球号码相加之和等于3中三等奖,两个小球号码相加之和不小于3中奖,
设“三等奖”事件为A,“中奖”的事件为B,
从四个小球任选两个共有
(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)六种不同的方法。………3分
(1)两个小球号码相加之和等于3的取法有2种:(0,3),(1,2)。
故。 ………6分
(2)法一:两个小球号码相加之和等于1的取法有1种:(0,1)
两个小球号码相加之和等于2的取法有1种:(0,2)。 ………9分
故 ………12分
法二:两个小球号码相加之和等于3的取法有2种:(0,3),(1,2); ………8分
两个小球号码相加之和等于4的取法有1种:(1,3); ………9分
两个小球号码相加之和等于5的取法有1种:(2,3); ………10分
故。
22.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.
(1)求事件“”的概率;
(2)求事件“”的概率.
解:设表示一个基本事件,则掷两次骰子包括:,,,,,,,,……,,,共36个基本事件.
(1)用表示事件“”,
则的结果有,,,共3个基本事件.
∴.
答:事件“”的概率为.
(2)用表示事件“”,
则的结果有,,,,,,,,共8个基本事件.
∴.
答:事件“”的概率为.
23.(12分)给出50个数,1,2,4,7,11,…,其规律是:第1
个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第
4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先
将下面给出的程序框图补充完整,再根据程序框图写出程序.
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (3分)
2. 程序:(6分)
二.练习题。
1.一个容量为20的样本数据,分组与各组内频数如下:(10,20),2;(20, 30),3;(30,40),4;(40,50),5;(50,60),4;(60,70],2.则样本在(10,50]上的频率为 ( C )
(A)90% (B)50% (C) 70% (D)25%
2.已知,,则( D )
A. B. C. D.
3.已知平面向量,,且,则( C )
A. B. C. D.
4.函数的最小值为( B )
A. B. C. D.
5.若( )
A. B. C. D.
6. 已知右图是函数的图象,那么( )
A. B.
C. D.
7.已知,,则 .-13
8.若=,=,则在上的投影为________________。
9.函数的单调递减区间是______________.
10.(12分)设计一个算法求:;试用流程图和相应程序表示.
11.将一枚骰子抛掷两次,若先后出现的点数分别为,则方程有实根的概率为( ) A B C D
12.(本小题满分14分)函数在同一个周期内,当 时取最大值1,当时,取最小值.
(1)求函数的解析式
(2)函数的图象经过怎样的变换可得到的图象?
(3)若函数满足方程求在内的所有实数根之和.
(2)
结 束
i= i +1
(1)
开 始
是
输出 s
否
i = 1
P = 1
S= 0
S= s + p
(2)
结 束
i= i +1
(1)
开 始
是
输出 s
否
i = 1
P = 1
S= 0
S= s + p
姓名_______________
一.基础知识练习题
1. 在抽取产品的尺寸过程中,将其尺寸分成若干组,是其中一组,抽查出的个体在该组上的频率为m ,该组上的直方图的高为h,则 ( )
A.hm B. C. D.h+m
2..现有辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,
时速在的汽车大约有( )
.辆 .辆 .辆 .80辆
3.已知,若0≤θ≤π,
使函数f(x)为偶函数的θ为 ( )
(A) (B) (C) (D)
4.某题的得分情况如下:其中众数是 ( )
得分/分 0 1 2 3 4
百分率/(%) 37.0 8.6 6.0 28.2 20.2
(A)37.0% (B)20.2% (C)0分 (D)4分
5.已知若则点的坐标为( )
6.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
再将所得的图象向左平移个单位,得到的图象对应的解析式是( )
A. B.
C. D.
7.. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是( )
A. B. C. D.
8. 在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是. ( )
A. B. C. D.
9. 一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )
A. B. C. D.
10.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是 ( )
(A) (B) (C) (D)
11. 6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A B. C. D.
12.有所有的两位数(10~99)中任取一个数,则这个数能被2或3整除的概率是( )
A. B. C. D.
13.(2009辽宁卷理)某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 h.
14.有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图
频率/组距
15.从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
16..将二进制数1010 101(2) 化为十进制结果为 ;
再将该数化为八进制数,结果为 .
17.将一颗骰子先后抛掷2次,观察向上的点数以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率为_____
19.(2009年广东卷文) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
20. 已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
21.购物广场拟在五一节举行抽奖活动,规则是:从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;
(2)求中奖的概率。
22.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.
(1)求事件“”的概率;
(2)求事件“”的概率.
23.(12分)给出50个数,1,2,4,7,11,…,其规律是:第1
个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第
4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先
将下面给出的程序框图补充完整,再根据程序框图写出程序.
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (3分)
2. 程序:(6分)
二.练习题。
1.一个容量为20的样本数据,分组与各组内频数如下:(10,20),2;(20, 30),3;(30,40),4;(40,50),5;(50,60),4;(60,70],2.则样本在(10,50]上的频率为 ( )
(A)90% (B)50% (C) 70% (D)25%
2.已知,,则( )
A. B. C. D.
3.已知平面向量,,且,则( )
A. B. C. D.
4.函数的最小值为( )
A. B. C. D.
5.若( )
A. B. C. D.
6. 已知右图是函数的图象,那么( )
A. B.
C. D.
7.已知,,则 .
8.若=,=,则在上的投影为________________。
9.函数的单调递减区间是______________.
10.(12分)设计一个算法求:;试用流程图和相应程序表示.
11.将一枚骰子抛掷两次,若先后出现的点数分别为,则方程有实根的概率为( )
A B C D
12.(本小题满分14分)函数在同一个周期内,当 时取最大值1,当时,取最小值.
(1)求函数的解析式
(2)函数的图象经过怎样的变换可得到的图象?
(3)若函数满足方程求在内的所有实数根之和.
综合练习题十一答案
一.基础知识练习题
1. 在抽取产品的尺寸过程中,将其尺寸分成若干组,是其中一组,抽查出的个体在该组上的频率为m ,该组上的直方图的高为h,则 ( B )
A.hm B. C. D.h+m
2..现有辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,
时速在的汽车大约有( C )
.辆 .辆 .辆 .80辆
3.已知,若0≤θ≤π,
使函数f(x)为偶函数的θ为
(A) (B) (C) (D)
4.某题的得分情况如下:其中众数是 ( C )
得分/分 0 1 2 3 4
百分率/(%) 37.0 8.6 6.0 28.2 20.2
(A)37.0% (B)20.2% (C)0分 (D)4分
5.已知若则点的坐标为(C )
6.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
再将所得的图象向左平移个单位,得到的图象对应的解析式是( C )
A. B.
C. D.
7.. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是(A)
A. B. C. D.
8. 在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是.
A. B. C. D.
9. 一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )
A. B. C. D.
10.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是 ( )
(A) (B) (C) (D)
11. 6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A B. C. D.
12.有所有的两位数(10~99)中任取一个数,则这个数能被2或3整除的概率是( )
A. B. C. D.
13.(2009辽宁卷理)某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共取100件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h,1020h,1032h,则抽取的100件产品的使用寿命的平均值为 h. 1013
14.有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图
解:(1)样本的频率分布表:
分组 频数 频率 频率∕组距
6 0.06 0.02
16 0.16 0.053
18 0.18 0.06
22 0.22 0.073
20 0.20 0.067
10 0.10 0.033
8 0.08 0.027
(2)频率分布直方图
频率/组距
0.073
0.020
12.5 15.5 18.5 21.5 24.5 27.5 30.5 33.5
频率折线图略
15.从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
16..将二进制数1010 101(2) 化为十进制结果为 85 ;
再将该数化为八进制数,结果为 . 125(8)
17.将一颗骰子先后抛掷2次,观察向上的点数以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率为_____
18. 10产品中有4件次品,从中任意取出2件,在所取得的产品中发现一件次品,则另一件也是次品的概率为___________
19.(2009年广东卷文) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高;(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
【解析】(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
20. 已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
解:记“甲射击一次,命中7环以下”为事件,“甲射击一次,命中7环”为事件,由于在一次射击中,与不可能同时发生,故与是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为,
由互斥事件的概率加法公式,.
答:甲射击一次,命中不足8环的概率是0.22.…………………………………6分
(2)方法1:记“甲射击一次,命中8环”为事件,“甲射击一次,命中9环(含9环)以上”为事件,则“甲射击一次,至少命中7环”的事件为,
∴.
答:甲射击一次,至少命中7环的概率为0.9.…………………………………12分
方法2:∵“甲射击一次,至少命中7环”为事件,
∴=1-0.1=0.9.
答:甲射击一次,至少命中7环的概率为0.9.………
21.购物广场拟在五一节举行抽奖活动,规则是:从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;
(2)求中奖的概率。
解:两个小球号码相加之和等于3中三等奖,两个小球号码相加之和不小于3中奖,
设“三等奖”事件为A,“中奖”的事件为B,
从四个小球任选两个共有
(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)六种不同的方法。………3分
(1)两个小球号码相加之和等于3的取法有2种:(0,3),(1,2)。
故。 ………6分
(2)法一:两个小球号码相加之和等于1的取法有1种:(0,1)
两个小球号码相加之和等于2的取法有1种:(0,2)。 ………9分
故 ………12分
法二:两个小球号码相加之和等于3的取法有2种:(0,3),(1,2); ………8分
两个小球号码相加之和等于4的取法有1种:(1,3); ………9分
两个小球号码相加之和等于5的取法有1种:(2,3); ………10分
故。
22.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.
(1)求事件“”的概率;
(2)求事件“”的概率.
解:设表示一个基本事件,则掷两次骰子包括:,,,,,,,,……,,,共36个基本事件.
(1)用表示事件“”,
则的结果有,,,共3个基本事件.
∴.
答:事件“”的概率为.
(2)用表示事件“”,
则的结果有,,,,,,,,共8个基本事件.
∴.
答:事件“”的概率为.
23.(12分)给出50个数,1,2,4,7,11,…,其规律是:第1
个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第
4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先
将下面给出的程序框图补充完整,再根据程序框图写出程序.
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (3分)
2. 程序:(6分)
二.练习题。
1.一个容量为20的样本数据,分组与各组内频数如下:(10,20),2;(20, 30),3;(30,40),4;(40,50),5;(50,60),4;(60,70],2.则样本在(10,50]上的频率为 ( C )
(A)90% (B)50% (C) 70% (D)25%
2.已知,,则( D )
A. B. C. D.
3.已知平面向量,,且,则( C )
A. B. C. D.
4.函数的最小值为( B )
A. B. C. D.
5.若( )
A. B. C. D.
6. 已知右图是函数的图象,那么( )
A. B.
C. D.
7.已知,,则 .-13
8.若=,=,则在上的投影为________________。
9.函数的单调递减区间是______________.
10.(12分)设计一个算法求:;试用流程图和相应程序表示.
11.将一枚骰子抛掷两次,若先后出现的点数分别为,则方程有实根的概率为( ) A B C D
12.(本小题满分14分)函数在同一个周期内,当 时取最大值1,当时,取最小值.
(1)求函数的解析式
(2)函数的图象经过怎样的变换可得到的图象?
(3)若函数满足方程求在内的所有实数根之和.
(2)
结 束
i= i +1
(1)
开 始
是
输出 s
否
i = 1
P = 1
S= 0
S= s + p
(2)
结 束
i= i +1
(1)
开 始
是
输出 s
否
i = 1
P = 1
S= 0
S= s + p
