9.4解直角三角形（1）

课件14张PPT。§9.4 解直角三角形（1）第9章 解直角三角形
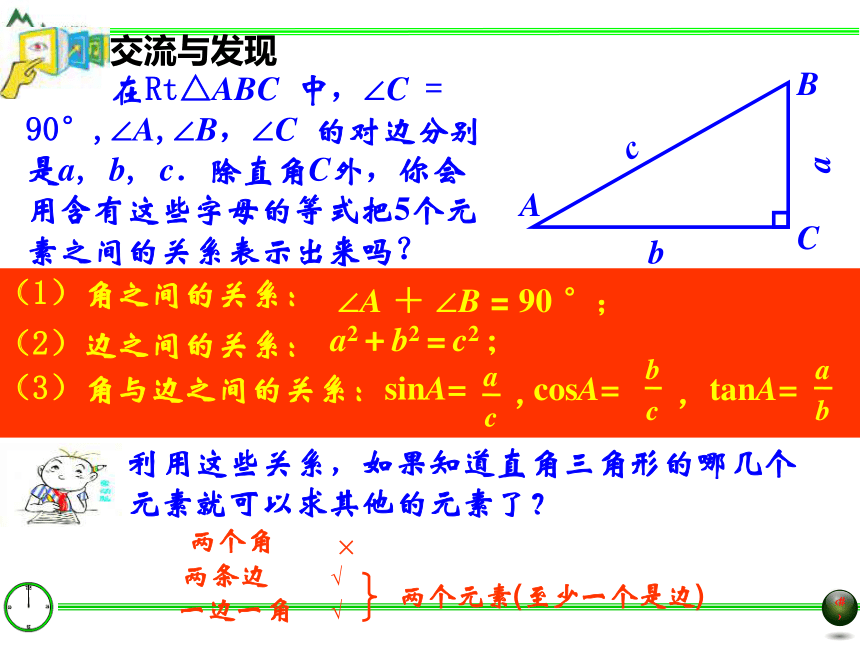
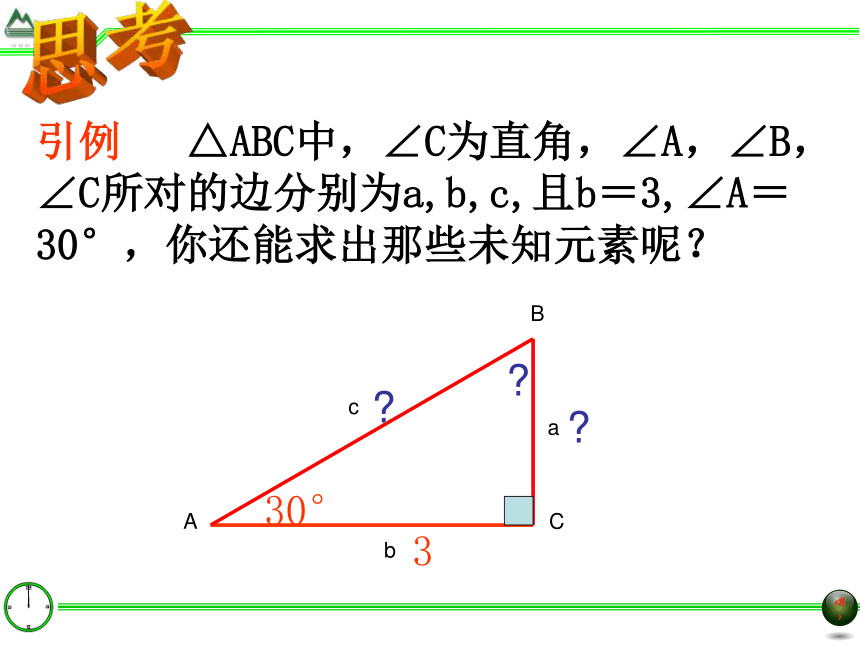
交流与发现利用这些关系，如果知道直角三角形的哪几个元素就可以求其他的元素了？ 在Rt△ABC 中，∠C = 90°,∠A,∠B，∠C 的对边分别是a, b, c．除直角C外，你会用含有这些字母的等式把5个元素之间的关系表示出来吗？∠A ＋ ∠B = 90 °；a2＋b2＝c2 ; （3）角与边之间的关系：（2）边之间的关系：（1）角之间的关系：，，两个元素(至少一个是边)两个角 两条边一边一角×√√引例 △ABC中，∠C为直角，∠A，∠B，∠C所对的边分别为a,b,c,且b＝3,∠A＝30°，你还能求出那些未知元素呢？ABCabc330°???思考六个元素三边两个锐角一个直角（已知）五个定义：
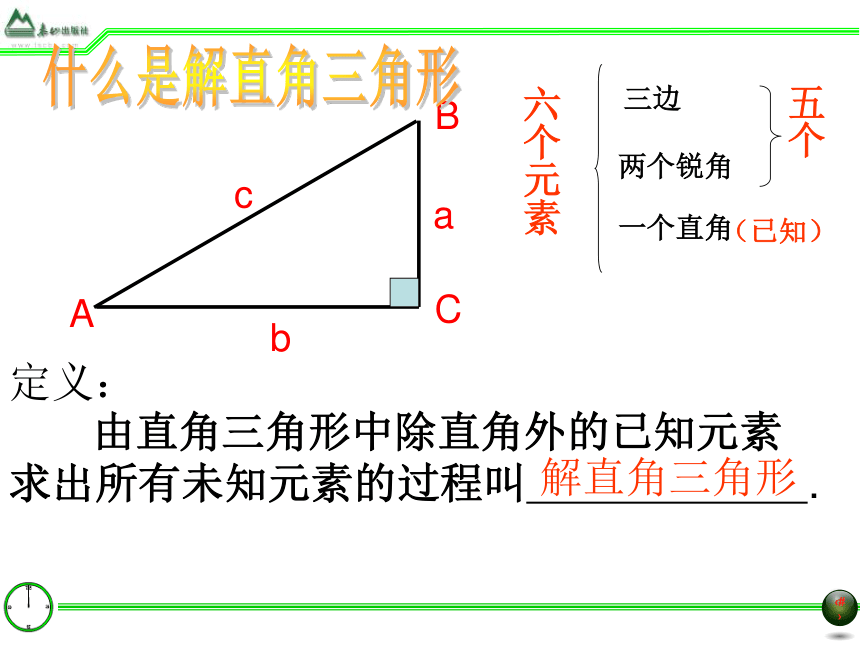
??? 由直角三角形中除直角外的已知元素求出所有未知元素的过程叫 . 解直角三角形什么是解直角三角形??? (1)三边之间的关系：
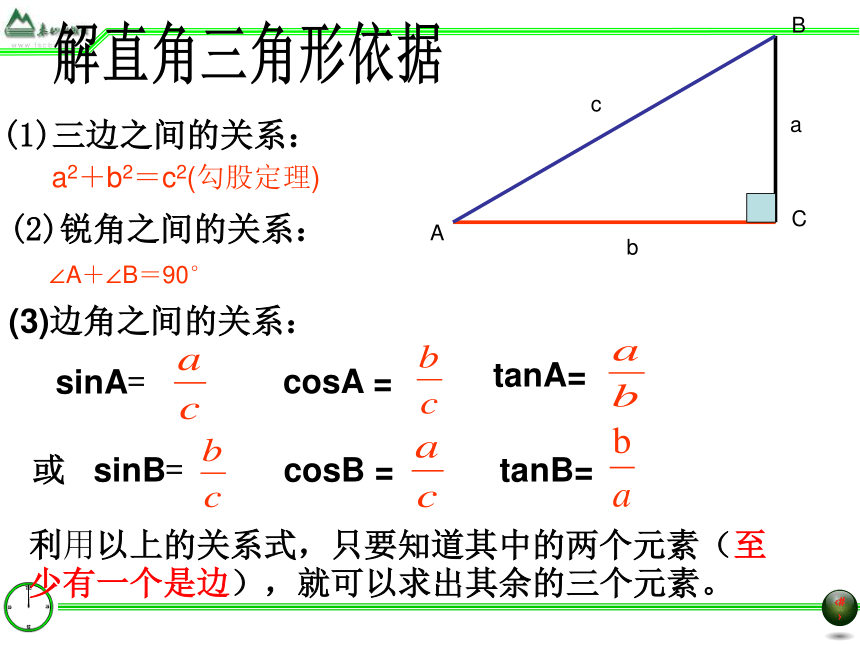
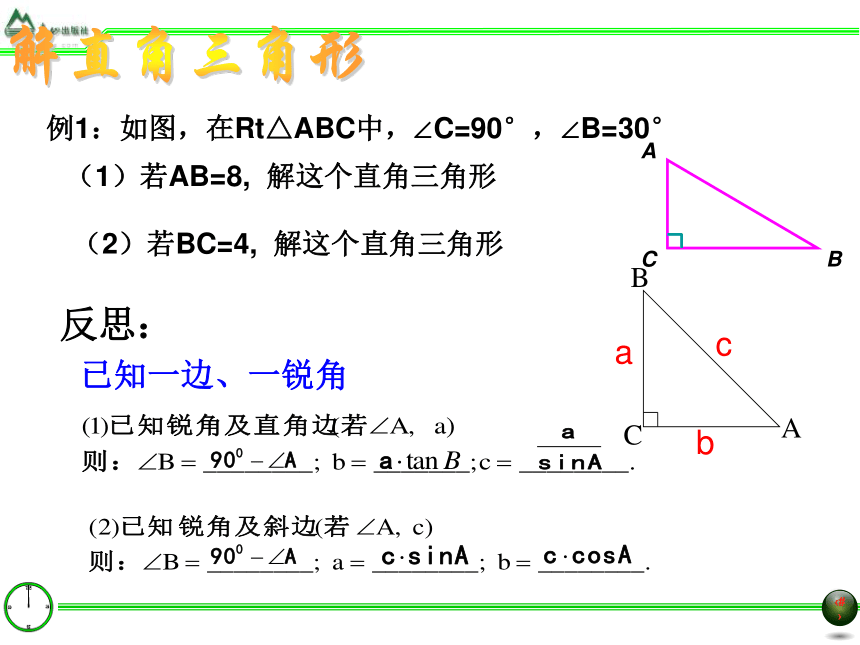
???????BCabcA(2)锐角之间的关系：　? a2＋b2＝c2(勾股定理) ∠A＋∠B＝90° (3)边角之间的关系： sinA=cosA =tanA=利用以上的关系式，只要知道其中的两个元素（至少有一个是边），就可以求出其余的三个元素。解直角三角形依据 或 sinB=cosB =tanB=例1：如图，在Rt△ABC中，∠C=90°，∠B=30°解直角三角形（1）若AB=8, 解这个直角三角形反思：已知一边、一锐角（2）若BC=4, 解这个直角三角形例2：如图，在Rt△ABC中，∠C=90°，
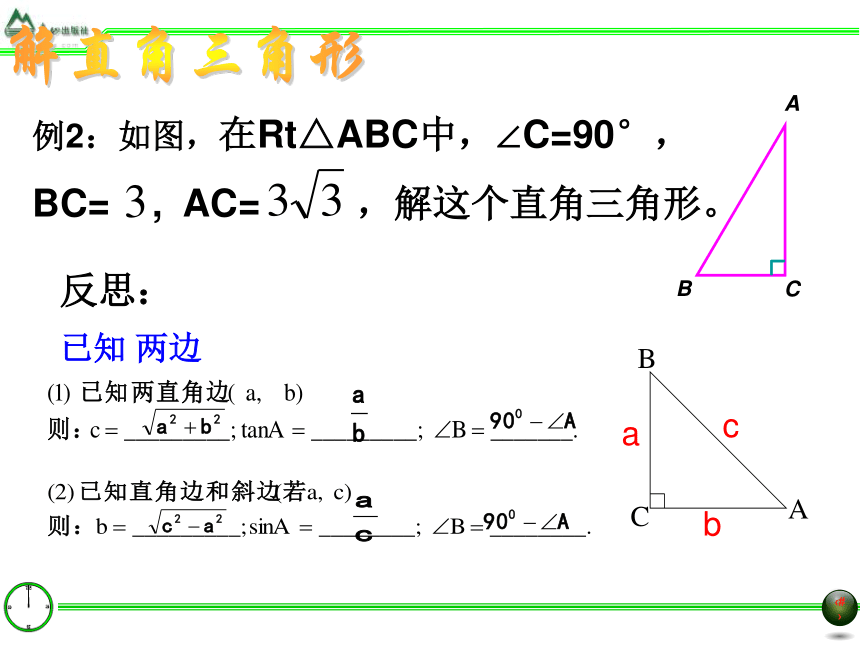
BC= , AC= ，解这个直角三角形。解直角三角形已知 两边反思：例3： 在Rt△ABC 中，已知∠C=90°，a = 17.5 ，c＝62.5 ．解这个直角三角形分析：这是已知直角三角形的两边解直角三角形的问题．
要会选择适当的三角比．A如图，在△ABC中，已知AC=6，
∠ C=75°，∠B=45°，
求:AB的长； 点睛：添加辅助线，“化斜为直”是我们常用的一种方法。尝试中考A B C 45°75°60°6D小结1、直角三角形解法2、点睛：在求解直角三角形有关问题时， 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据，以防止“累积误差”和“一错再错”∠A ＋ ∠B = 90 °；a2＋b2＝c2 ; （3）角与边之间的关系：（2）边之间的关系：（1）角之间的关系：2. 如果知道直角三角形的几个元素就可以求其他的元素？
有几种情况？两个元素(至少一个是边)两条边或一边一角1.直角三角形的边角关系：课堂小结3、优选关系式4、点睛：在求解直角三角形有关问题时， 要先画出图形以利于分析解决问题。
选择关系式时要尽量利用原始数据，以防止“累积误差”和“一错再错” 思考练习题1、已知在△ABC中,∠C＝９０o ∠A=60o ，BC=5，BD是中线，则BD的长为_______
2、在△ABC中 ∠C＝９０o ，CD ⊥AB 于D
AD=4， sin ∠ACD= , CD=__BC=__
求b,c,tanB；

(2)a＋C＝12，b＝8，求a，c，cosB
3、 △ABC中，∠C＝90°，a、b、c分别为∠A、∠B、∠C的对边，
(1)a＝4,，sinA＝