3.2.2相交线所成的角
图片预览



文档简介
课件13张PPT。3.3.2相交直线所成的角1.理解二线四角。
2.理解三线八角。1.内容:54页到56页;时间:5分钟。
2.自学思考题:
(1)什么叫邻补角?
(2)什么叫对顶角?它有什么性质?
(3)同位角,内错角,同旁内角各有什么特征?
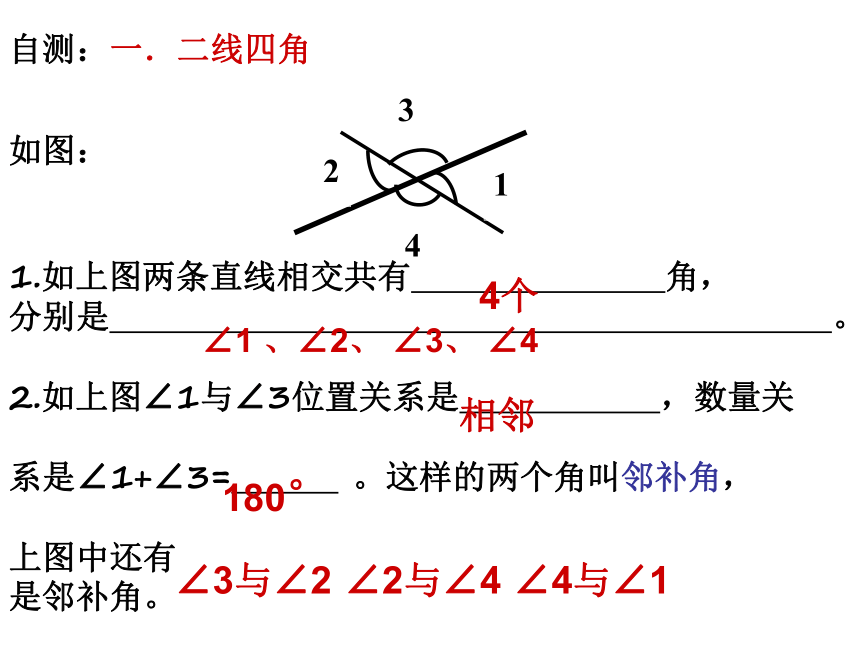
(4)自学完后完成学案中的自测部分(8分钟)〖学习目标〗〖自学指导〗〖小组合作〗 (5分钟) 团结就是力量!快乐参与,快乐成长!积极行动! 看哪一组动作快,效果好!如图:1.如上图两条直线相交共有 角,
分别是 。
2.如上图∠1与∠3位置关系是 ,数量关
系是∠1+∠3= 。这样的两个角叫邻补角,
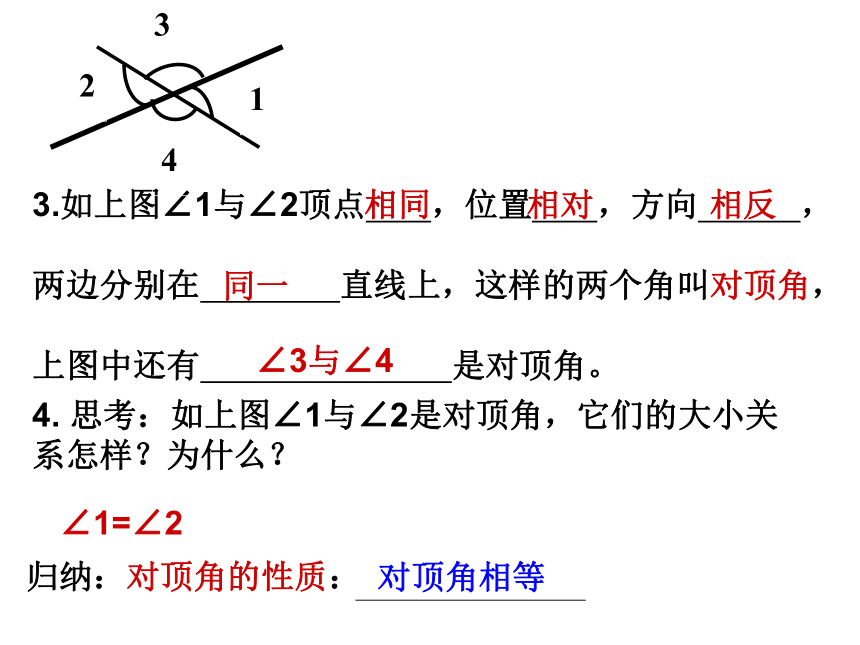
上图中还有 是邻补角。自测:一.二线四角4个∠1 、∠2、 ∠3、 ∠4相邻180°∠3与∠2∠2与∠4∠4与∠13.如上图∠1与∠2顶点 ,位置 ,方向 ,
两边分别在 直线上,这样的两个角叫对顶角,
上图中还有 是对顶角。
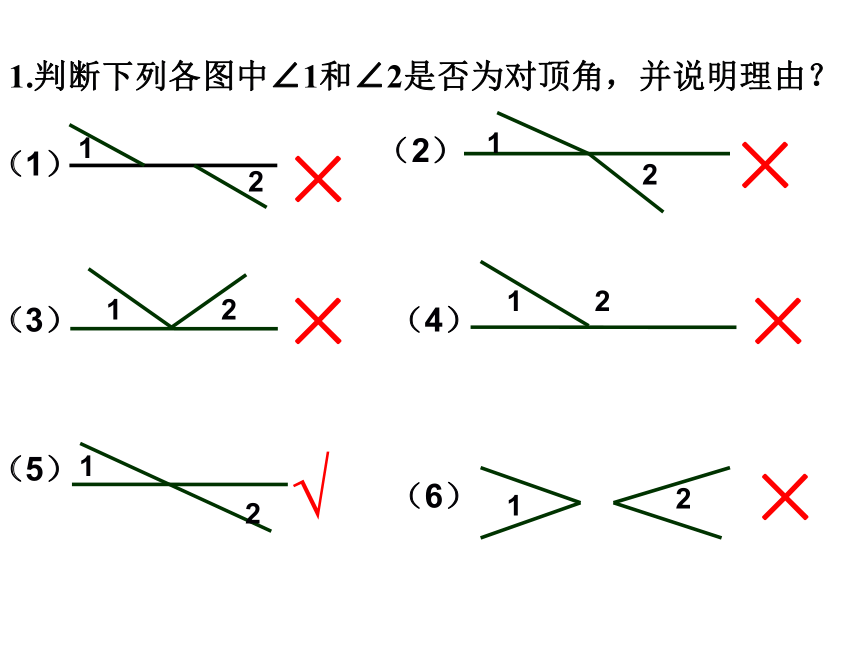
归纳:对顶角的性质:相同相对相反同一∠3与∠4对顶角相等4. 思考:如上图∠1与∠2是对顶角,它们的大小关系怎样?为什么?∠1=∠22212121212(1)(2)(3)(4)(5)(6)111.判断下列各图中∠1和∠2是否为对顶角,并说明理由?×××××√如图(1)三线是:被截直线是 ,截线是 ;
八角是: 。
2.先看图(1)中∠1和∠5,它们分别在被截直线AB、
CD的 方,并且都在截线EF的 侧,像这样位
置相同的一对角叫做 。
同位角的特征是:在被截直线的 ,在截线的 。
如图(1):二.三线八角在图(1)中,还有 也是同位角。AB和CD直线EF∠1 、∠2、 ∠3、 ∠4 ∠5 、∠6、 ∠7、∠8上或同同同位角同方同侧∠4和∠8∠2和∠7∠3和∠63.再看∠3与∠5,它们都在被截直线 AB、CD ,且∠3在截线EF 侧,∠5在截线EF 侧,像这样的一对角叫做 。
内错角的特征是:在被截直线 ,在截线的 。
在图(1)中,还有 也是内错角。如图(1):二.三线八角之间左右内错角之间异侧∠4与∠64.在图(1)中,∠3和∠6在被截直线AB、CD ,但它们在截线EF的 像这样的一对角,我们称它为 。
旁内角的特征是:在被截直线 ,在截线的 。
在图(1)中,还有 也是同旁内角。如图(1):二.三线八角之间同旁旁内角之间同旁∠4和∠52.下图中,∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?它们各是什么角? ∠1与∠2是直线AB截直线DE,BC而成的,它们是同位角。∠3与∠4是直线DE截直线AB,AC而成的,它们是同旁内角。∠1与∠2是直线BD截直线DE,AC而成的,它们是内错角。∠3与∠4是直线AC截直线AE,BD而成的,它们是同旁内角。∠1与∠2是直线AC截直线DC,AB而成的,它们是内错角。∠3与∠4是直线AC截直线AD,BC而成的,它们是内错角。例1.如图,直线DE交∠ABC的边BA于点F,如果∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由
〖课堂小结〗这节课你学会了什么?你还存什么问题?〖达标训练〗
2.理解三线八角。1.内容:54页到56页;时间:5分钟。
2.自学思考题:
(1)什么叫邻补角?
(2)什么叫对顶角?它有什么性质?
(3)同位角,内错角,同旁内角各有什么特征?
(4)自学完后完成学案中的自测部分(8分钟)〖学习目标〗〖自学指导〗〖小组合作〗 (5分钟) 团结就是力量!快乐参与,快乐成长!积极行动! 看哪一组动作快,效果好!如图:1.如上图两条直线相交共有 角,
分别是 。
2.如上图∠1与∠3位置关系是 ,数量关
系是∠1+∠3= 。这样的两个角叫邻补角,
上图中还有 是邻补角。自测:一.二线四角4个∠1 、∠2、 ∠3、 ∠4相邻180°∠3与∠2∠2与∠4∠4与∠13.如上图∠1与∠2顶点 ,位置 ,方向 ,
两边分别在 直线上,这样的两个角叫对顶角,
上图中还有 是对顶角。
归纳:对顶角的性质:相同相对相反同一∠3与∠4对顶角相等4. 思考:如上图∠1与∠2是对顶角,它们的大小关系怎样?为什么?∠1=∠22212121212(1)(2)(3)(4)(5)(6)111.判断下列各图中∠1和∠2是否为对顶角,并说明理由?×××××√如图(1)三线是:被截直线是 ,截线是 ;
八角是: 。
2.先看图(1)中∠1和∠5,它们分别在被截直线AB、
CD的 方,并且都在截线EF的 侧,像这样位
置相同的一对角叫做 。
同位角的特征是:在被截直线的 ,在截线的 。
如图(1):二.三线八角在图(1)中,还有 也是同位角。AB和CD直线EF∠1 、∠2、 ∠3、 ∠4 ∠5 、∠6、 ∠7、∠8上或同同同位角同方同侧∠4和∠8∠2和∠7∠3和∠63.再看∠3与∠5,它们都在被截直线 AB、CD ,且∠3在截线EF 侧,∠5在截线EF 侧,像这样的一对角叫做 。
内错角的特征是:在被截直线 ,在截线的 。
在图(1)中,还有 也是内错角。如图(1):二.三线八角之间左右内错角之间异侧∠4与∠64.在图(1)中,∠3和∠6在被截直线AB、CD ,但它们在截线EF的 像这样的一对角,我们称它为 。
旁内角的特征是:在被截直线 ,在截线的 。
在图(1)中,还有 也是同旁内角。如图(1):二.三线八角之间同旁旁内角之间同旁∠4和∠52.下图中,∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?它们各是什么角? ∠1与∠2是直线AB截直线DE,BC而成的,它们是同位角。∠3与∠4是直线DE截直线AB,AC而成的,它们是同旁内角。∠1与∠2是直线BD截直线DE,AC而成的,它们是内错角。∠3与∠4是直线AC截直线AE,BD而成的,它们是同旁内角。∠1与∠2是直线AC截直线DC,AB而成的,它们是内错角。∠3与∠4是直线AC截直线AD,BC而成的,它们是内错角。例1.如图,直线DE交∠ABC的边BA于点F,如果∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由
〖课堂小结〗这节课你学会了什么?你还存什么问题?〖达标训练〗
