特殊平行四边形教案
图片预览
文档简介
特殊平行四边形复习(教案)
马良中心学校 乔兆权
教学目标:
(1) 认知目标:使学生掌握特殊平行四边形的性质与判定,并会运用特殊平行四边形的性质与判定解(证)题。
(2) 能力目标:通过作图、操作说理培养学生用数学语言规范表达的能力,培养学生观察、分析、猜想、归纳知识的自学能力和培养学生类比、转化、推导、论证的数学思维品质。
(3) 情感目标:渗透从具体到抽象,特殊到一般的数学思想以及事物之间互相转化的辨证观点。
教学重点:矩形、菱形、正方形与平行四边形的性质的区别与联系;三种特殊平行四边形的判定的运用;能熟练运用特殊平行四边形的性质与判定解(证)题。
教学难点:运用特殊平行四边形的性质与判定解决有关问题。
教法:以学生的合作探究为主体,教师的适时引导为辅的教学方式。采用类比、归纳的方法让学生比较特殊平行四边形的性质和判定的异同和联系,帮助学生掌握知识。
学法: 学生始终以"自主、合作、探究"为主要学习方式。真正做到课堂教学中面向全体学生。
教学过程
1. 基础知识回顾
二.基本练习
四.感悟与小结:本节课你学到了什么?
五.能力检测
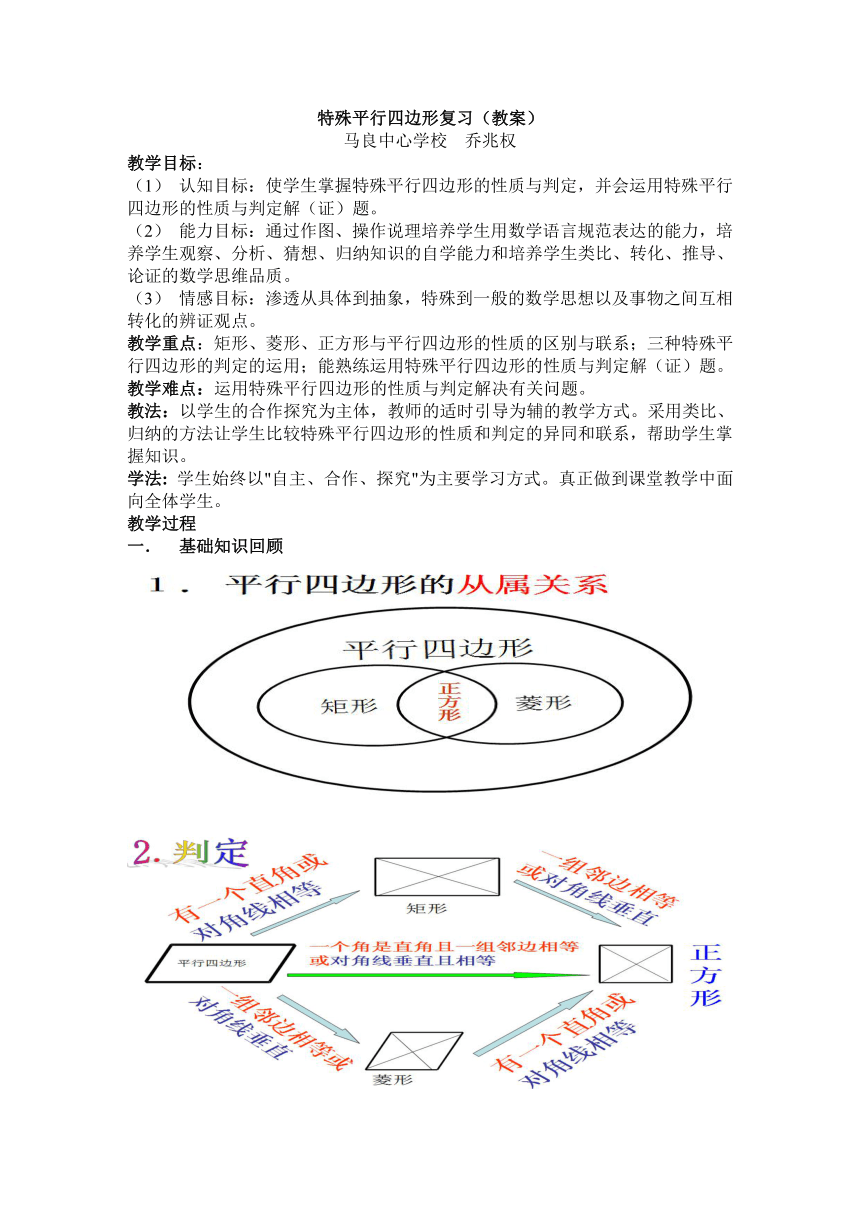
平行四边形的从属关系
行四边形
形(彩菱形
2.判定
矩形
公
个角是直角且一组邻边相等
平行四边形
对角线垂直且相等
菱形
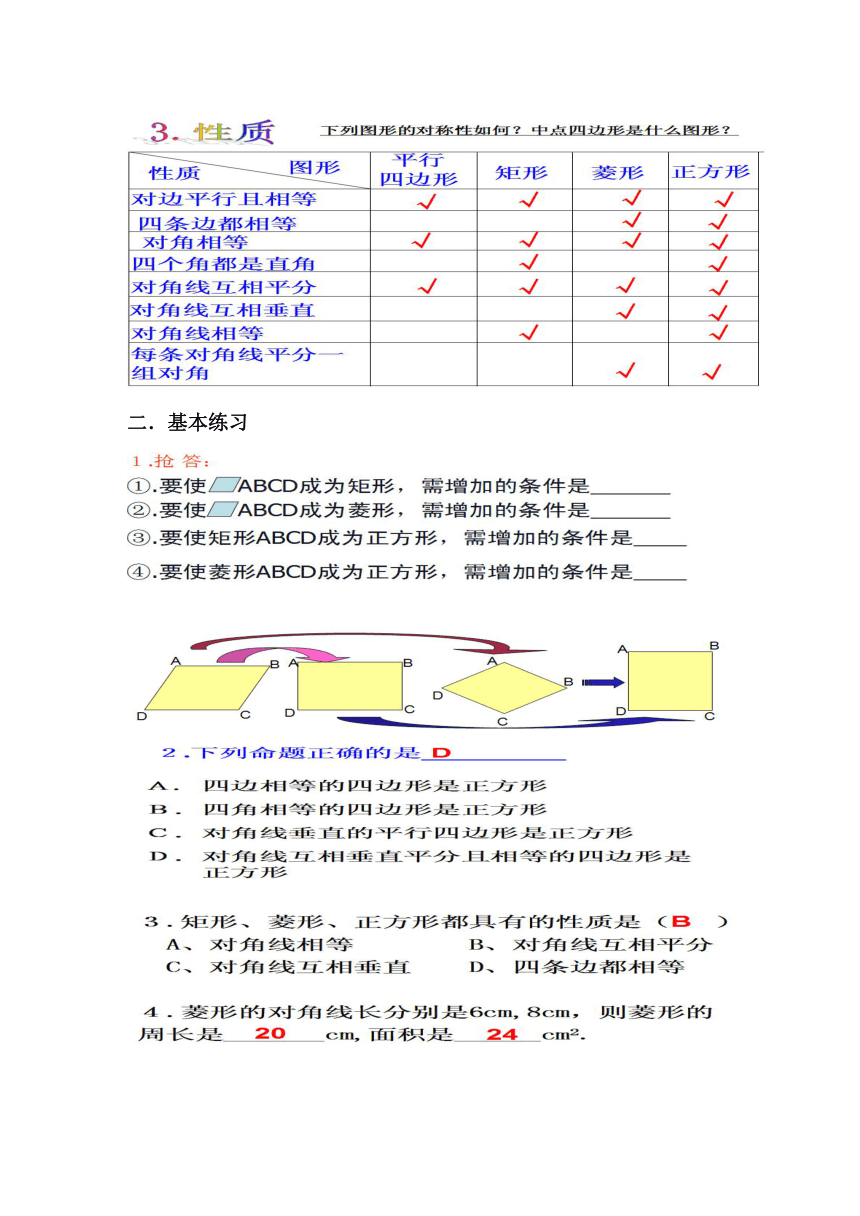
3.性质
下列图形的对称性如何 中点四边形是什么图形
图形
平行
性质
四边形矩形「菱形正方形
对边平行且相等
四条边都相等
对角相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
每条对角线平分
组对角
抢
要使ABCD成为矩形,需增加的条件
使□ABCD成为菱形,需增加的条
使矩形ABCD成为正方形,需增加的条件是
④要使菱形ABCD成为正方形,需增加的条件是
列命题正确的是D
A.四边相等的四边形是正方形
角相等的四边形是正方形
对角线垂直的平行四边形是正方形
对角线互相垂直平分且相等的四边形是
正方形
3.矩形、菱形、正方形都具有的性质是(B)
A、对角线相等
对角线互相平
C、对角线互相垂直
条边都相等
4.菱形的对角线长分别是6cm,8cm,则菱形的
周长是20cm,面积是
5如图,菱形ABCD的对角线
的长分别为2和5,P是对角线
AC上任一点(点P不与点A
重合)且PE∥BC交AB
交AD于F,则阴
影部分的面积
例题剖析
例1如图,矩形ABCD的对角线C、BD交于点
D作DP∥OC
P=OC,连结CP,试
判断四边形CODP的形状
析
得四边形CODP是平行四边形
再由四边形ABCD是矩形,得OC
得出四边形C
菱形。
解:四边形CODP是菱形
DPlOC, DP=OC
四边形CODP是平行四边形
四边形ABCD是矩形
CO=DO
四边形CODP是菱形
马良中心学校 乔兆权
教学目标:
(1) 认知目标:使学生掌握特殊平行四边形的性质与判定,并会运用特殊平行四边形的性质与判定解(证)题。
(2) 能力目标:通过作图、操作说理培养学生用数学语言规范表达的能力,培养学生观察、分析、猜想、归纳知识的自学能力和培养学生类比、转化、推导、论证的数学思维品质。
(3) 情感目标:渗透从具体到抽象,特殊到一般的数学思想以及事物之间互相转化的辨证观点。
教学重点:矩形、菱形、正方形与平行四边形的性质的区别与联系;三种特殊平行四边形的判定的运用;能熟练运用特殊平行四边形的性质与判定解(证)题。
教学难点:运用特殊平行四边形的性质与判定解决有关问题。
教法:以学生的合作探究为主体,教师的适时引导为辅的教学方式。采用类比、归纳的方法让学生比较特殊平行四边形的性质和判定的异同和联系,帮助学生掌握知识。
学法: 学生始终以"自主、合作、探究"为主要学习方式。真正做到课堂教学中面向全体学生。
教学过程
1. 基础知识回顾
二.基本练习
四.感悟与小结:本节课你学到了什么?
五.能力检测
平行四边形的从属关系
行四边形
形(彩菱形
2.判定
矩形
公
个角是直角且一组邻边相等
平行四边形
对角线垂直且相等
菱形
3.性质
下列图形的对称性如何 中点四边形是什么图形
图形
平行
性质
四边形矩形「菱形正方形
对边平行且相等
四条边都相等
对角相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
每条对角线平分
组对角
抢
要使ABCD成为矩形,需增加的条件
使□ABCD成为菱形,需增加的条
使矩形ABCD成为正方形,需增加的条件是
④要使菱形ABCD成为正方形,需增加的条件是
列命题正确的是D
A.四边相等的四边形是正方形
角相等的四边形是正方形
对角线垂直的平行四边形是正方形
对角线互相垂直平分且相等的四边形是
正方形
3.矩形、菱形、正方形都具有的性质是(B)
A、对角线相等
对角线互相平
C、对角线互相垂直
条边都相等
4.菱形的对角线长分别是6cm,8cm,则菱形的
周长是20cm,面积是
5如图,菱形ABCD的对角线
的长分别为2和5,P是对角线
AC上任一点(点P不与点A
重合)且PE∥BC交AB
交AD于F,则阴
影部分的面积
例题剖析
例1如图,矩形ABCD的对角线C、BD交于点
D作DP∥OC
P=OC,连结CP,试
判断四边形CODP的形状
析
得四边形CODP是平行四边形
再由四边形ABCD是矩形,得OC
得出四边形C
菱形。
解:四边形CODP是菱形
DPlOC, DP=OC
四边形CODP是平行四边形
四边形ABCD是矩形
CO=DO
四边形CODP是菱形
