锐角三角函数

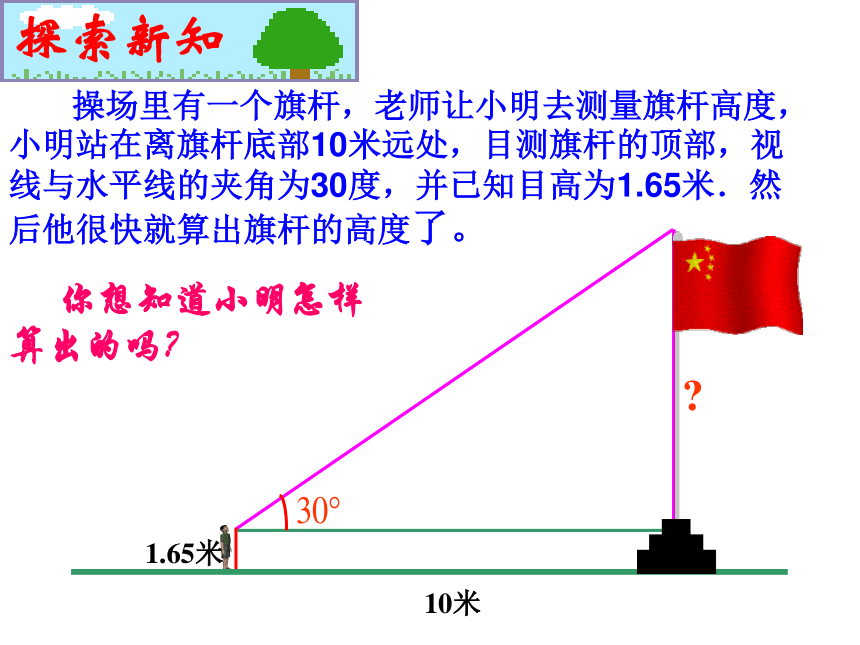
课件11张PPT。 §19.3.1 锐角三角函数 操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30度，并已知目高为1.65米．然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗？直角三角形中边角的再认识如图，Rt△ABC中： 找一找
如图，在Rt△MNP中，∠N＝90°.
∠P的对边是_________,∠P的邻边是_______;
∠M的对边是________ ,∠M的邻边是_______;MNPNPNMN如图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3，
∵ Rt△AB1C1∽Rt△_______∽Rt△________
∴　 = =AB3C3AB2C2探索一B4思考：
在Rt△ABC中，对于锐角A的每一个确定的值，
①∠A的对边与斜边的比值与△ABC的边长大小有关系吗？ ②∠A的邻边与斜边的比值呢？
③∠A的对边与邻边的比值呢？
④∠A的邻边与对边的比值呢？
由此可见：
在Rt△ABC中，对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值是惟一确定的.
????????? 这几个比值都是锐角∠A的函数，记作
sinA、cosA、tanA、cotA，即
sinA = cosA = tanA = cotA = 锐角∠A的正弦、余弦、正切、余切函数，统称为锐角∠A的三角函数.
概括正弦余弦正切余切例 求出如图所示的Rt△ABC中∠A的四个三角函数值. 解：∵ ∴ sinA = cosA = tanA = cotA = 17 求出如图所示的Rt△DEC（∠E＝90°）中∠D的四个三角函数值.
牛刀小试 解：　∵ ∴ sinD=
cosD= tanD= cotD= 8 操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部10米远处，目测旗杆的顶部，视线与水平线的夹角为30度，并已知目高为1.65米．然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗？sinA = cosA = tanA = cotA = 概括正弦余弦正切余切3、锐角α的三角函数值的取值范围 。正弦 0＜ sinα＜1 正切 tanα>0
余弦 0＜ cosα＜1 余切 cotα>0
在Rt△ABC中,∠C＝Rt∠,我们把: sin A= cos A= tan A= cot A= 分别叫做锐角∠A的正弦、余弦、正切、余切，统称为锐角∠A的三角函数.(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积
(3) sinA 是一个比值 (4)sinA 没有单位总结