相似三角形的判定（3）

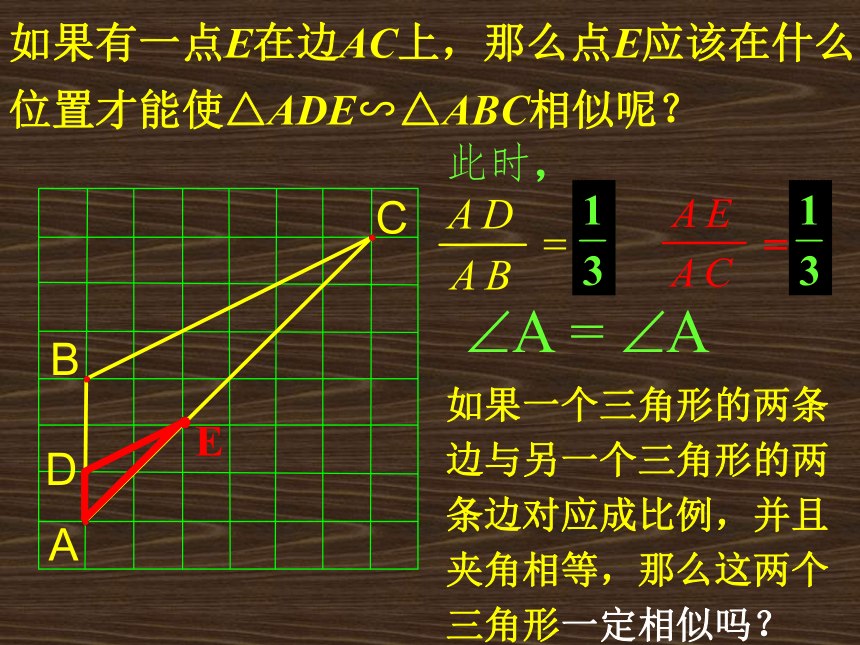
课件13张PPT。相似三角形的判定(3)相似三角形的判定判断两个三角形相似,你有哪些方法方法1：通过定义（不常用）方法2：通过平行线。方法3：三边对应成比例。如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE∽△ABC相似呢？ 此时，如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形一定相似吗？ 已知:如图△ABC和△A`B`C`中,∠A＝∠A` , ∠A` ,A`B`:AB=A`C`:AC.
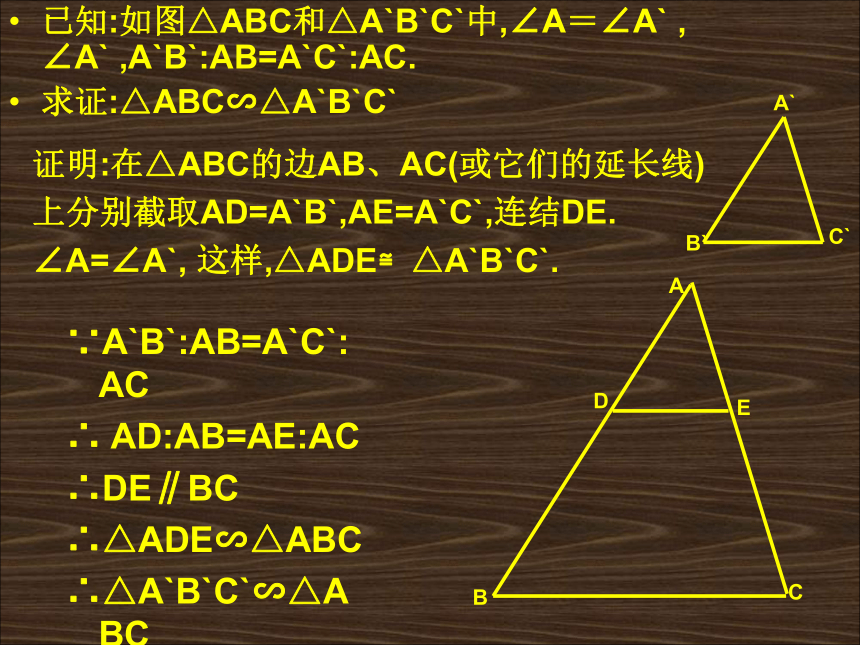
求证:△ABC∽△A`B`C`ABCED证明:在△ABC的边AB、AC(或它们的延长线)
上分别截取AD=A`B`,AE=A`C`,连结DE.
∠A=∠A`, 这样,△ADE≌△A`B`C`.∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A`B`C`∽△ABC相似三角形的识别 如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似 。(两边对应成比例且夹角相等，两三角形相似)A想一想：如果对应相等的角不是两条对应边的夹角，那么两个三角形是否相似呢？1、已知△ABC和 △A’B’C’,根据下列条件
判断它们是否相似.(2) ∠A＝45°，AB=12cm， AC=15cm
∠A’＝45°，A’B’＝16cm，A’C’＝20cm（1）∠A=120°,AB=7cm,AC=14cm,
∠A`=120°,A`B`=3cm,A`C`=6cm;2、判断图中△AEB和△FEC是否相似？ 解：∴△AEB∽△FEC ∵∠1＝∠2123.在正方形ABCD中，E为AD上的中点, F是AB的四分一等分点，连结EF、EC；△AEF与△DCE是否相似?说明理由.4、已知：如图，BD、CE是△ABC的高，
试说明 △ADE∽△ABC。? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.再见