3.4 基本不等式
图片预览





文档简介
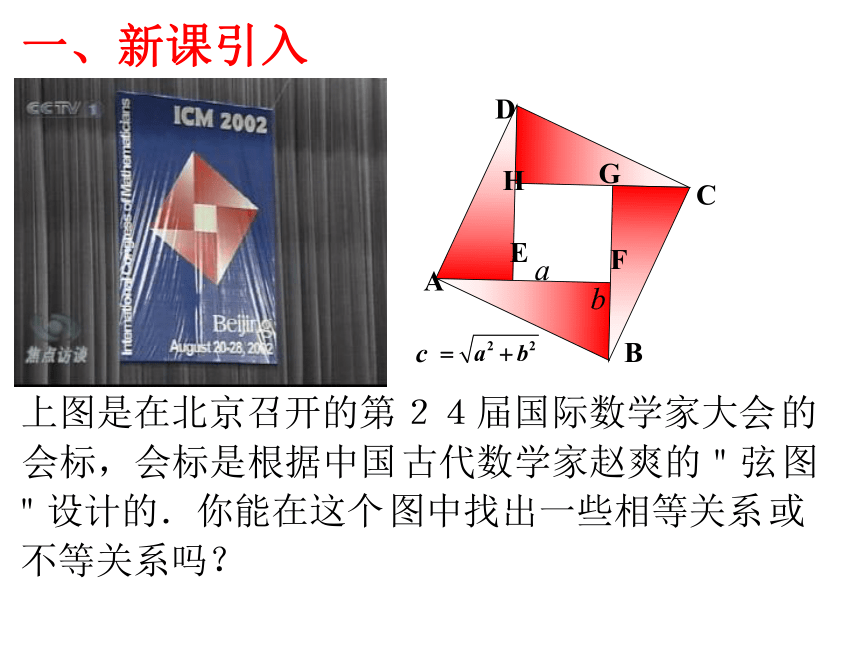
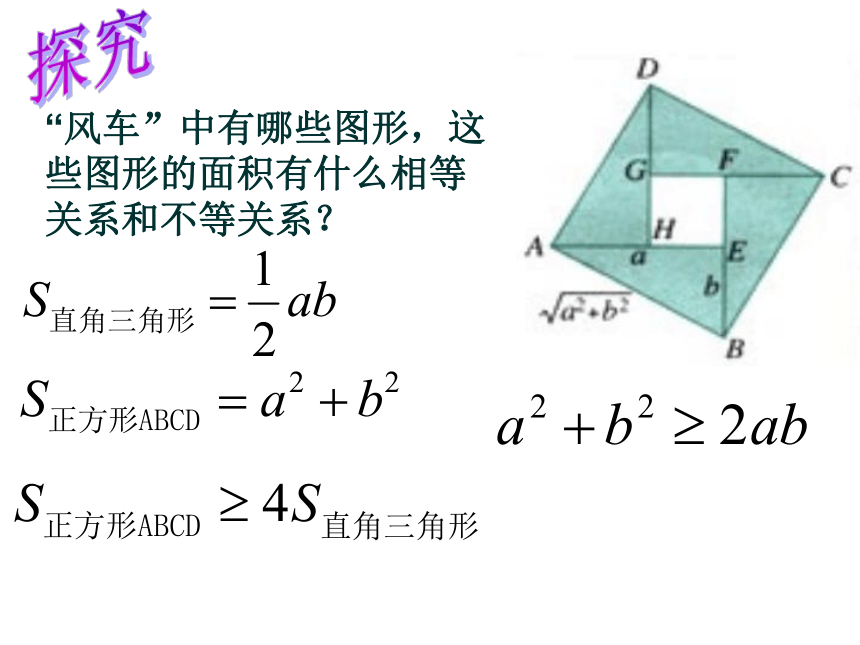
课件20张PPT。§3.4基本不等式2002年国际数学家大会会标 创设情境、体会感知:三国时期吴国数学家赵爽一、新课引入ADCBHGFE“风车”中有哪些图形,这些图形的面积有什么相等关系和不等关系?探究问:那么它们有相等的情况吗?
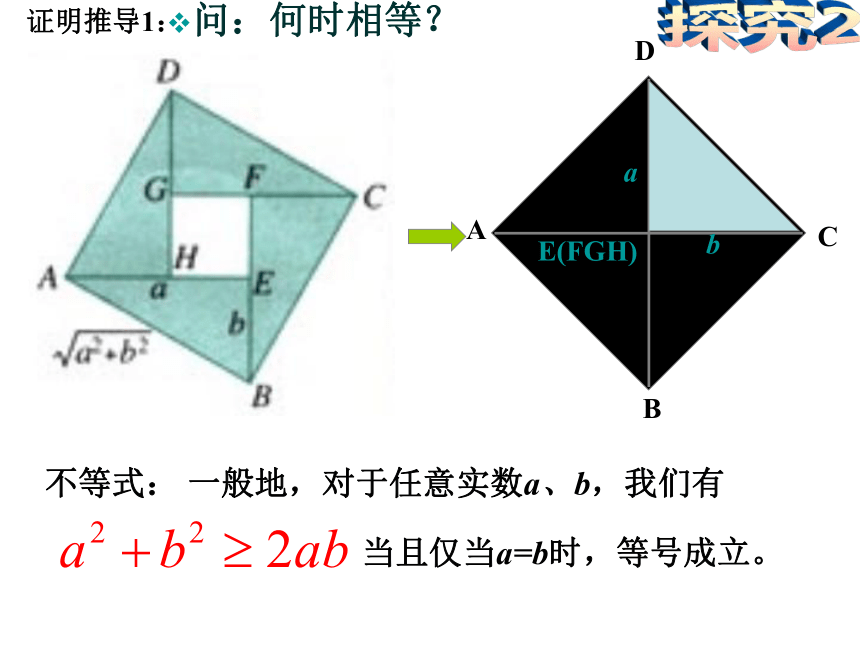
证明推导1:问:何时相等?探究2结论:一般地,对于任意实数a、b,我们有
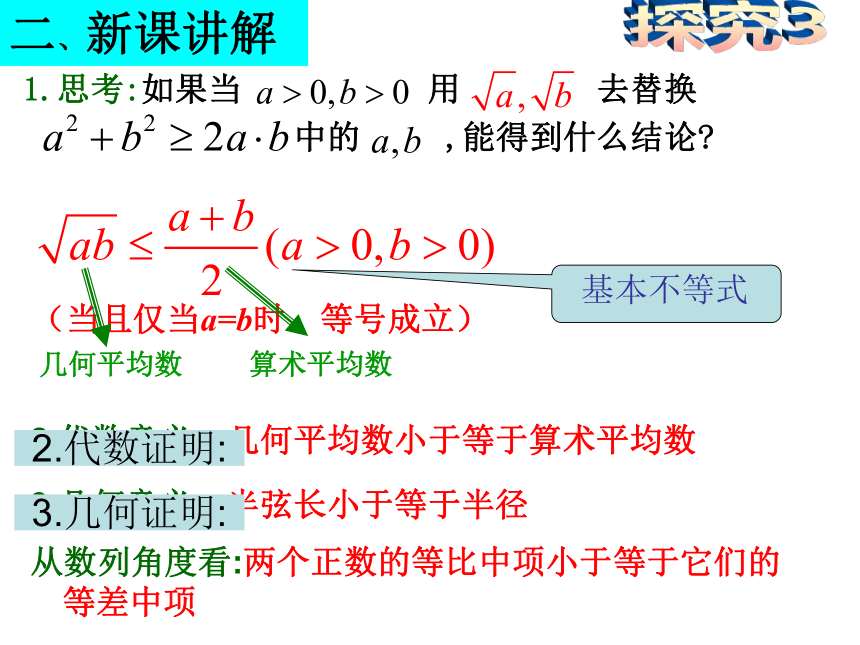
当且仅当a=b时,等号成立当a,b为任意实数时, 还成立吗?形数此不等式称为重要不等式2.代数意义:几何平均数小于等于算术平均数2.代数证明:3.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立)二、新课讲解3.几何证明:从数列角度看:两个正数的等比中项小于等于它们的等差中项1.思考:如果当 用 去替换
中的 ,能得到什么结论? 基本不等式探究3基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。例1.用篱笆围一个面积为 的矩形菜园, 问该矩形的长、宽各为多少时, 所用篱笆最短,最短的篱笆是多少?三、应用解: (1)设矩形菜园的长为 ,宽为 , 则 , 篱笆的长为 . 由(2)一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长,宽各为多少时,菜园的面积最大,最大面积是多少?已知a,b都是正数,
(1)若ab是定值P, 则当a=b时,
a+b有最小值 ;
(2)若a+b是定值S, 则当a=b
时,ab有最大值 ;
利用基本不等式求最值(均值不等式定理)积一定,和有最小值; 和一定,积有最大值。积一定,和有最小值; 和一定,积有最大值。注意:一正二定三相等!1、本节课主要内容?你会了吗?五 、小结2、两个结论:两个正数,积定和最小;和定积最大。构造条件三、应用例1、若 ,求 的最小值.变3:若 ,求 的最小值.变2:若 ,求 的最小值.发现运算结构,应用不等式问:在结论成立的基础上,条件“a>0,b>0”可以变化吗?变1:若 求 的最小值三、应用例2、已知 ,求函数 的最大值.变式:已知 ,求函数 的最大值.发现运算结构,应用不等式应用要点:
一正数 二定值 三相等结论1:两个正数积为定值,则和有最小值结论2:两个正数和为定值,则积有最大值3.已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?
4.用20cm长的铁丝折成一个面积最大的矩形,应怎样折? 四 、巩固大933小证明:要证只要证 ( )① ② 要证②,只要证 ( )③ 要证③,只要证( - ) ④证明:当 时, . 探究3作业课本P100习题3.4A组
第1,2题再见!oabABPQ1.如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=__ __,半径AO=_____几何意义:圆的半径不小于圆内半弦长探究4你能用这个图得出基本不等式的几何解释吗?2.PQ与AO的大小关系怎样?
证明推导1:问:何时相等?探究2结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立当a,b为任意实数时, 还成立吗?形数此不等式称为重要不等式2.代数意义:几何平均数小于等于算术平均数2.代数证明:3.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立)二、新课讲解3.几何证明:从数列角度看:两个正数的等比中项小于等于它们的等差中项1.思考:如果当 用 去替换
中的 ,能得到什么结论? 基本不等式探究3基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。例1.用篱笆围一个面积为 的矩形菜园, 问该矩形的长、宽各为多少时, 所用篱笆最短,最短的篱笆是多少?三、应用解: (1)设矩形菜园的长为 ,宽为 , 则 , 篱笆的长为 . 由(2)一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长,宽各为多少时,菜园的面积最大,最大面积是多少?已知a,b都是正数,
(1)若ab是定值P, 则当a=b时,
a+b有最小值 ;
(2)若a+b是定值S, 则当a=b
时,ab有最大值 ;
利用基本不等式求最值(均值不等式定理)积一定,和有最小值; 和一定,积有最大值。积一定,和有最小值; 和一定,积有最大值。注意:一正二定三相等!1、本节课主要内容?你会了吗?五 、小结2、两个结论:两个正数,积定和最小;和定积最大。构造条件三、应用例1、若 ,求 的最小值.变3:若 ,求 的最小值.变2:若 ,求 的最小值.发现运算结构,应用不等式问:在结论成立的基础上,条件“a>0,b>0”可以变化吗?变1:若 求 的最小值三、应用例2、已知 ,求函数 的最大值.变式:已知 ,求函数 的最大值.发现运算结构,应用不等式应用要点:
一正数 二定值 三相等结论1:两个正数积为定值,则和有最小值结论2:两个正数和为定值,则积有最大值3.已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?
4.用20cm长的铁丝折成一个面积最大的矩形,应怎样折? 四 、巩固大933小证明:要证只要证 ( )① ② 要证②,只要证 ( )③ 要证③,只要证( - ) ④证明:当 时, . 探究3作业课本P100习题3.4A组
第1,2题再见!oabABPQ1.如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=__ __,半径AO=_____几何意义:圆的半径不小于圆内半弦长探究4你能用这个图得出基本不等式的几何解释吗?2.PQ与AO的大小关系怎样?
