锐角三角函数(2)
图片预览



文档简介
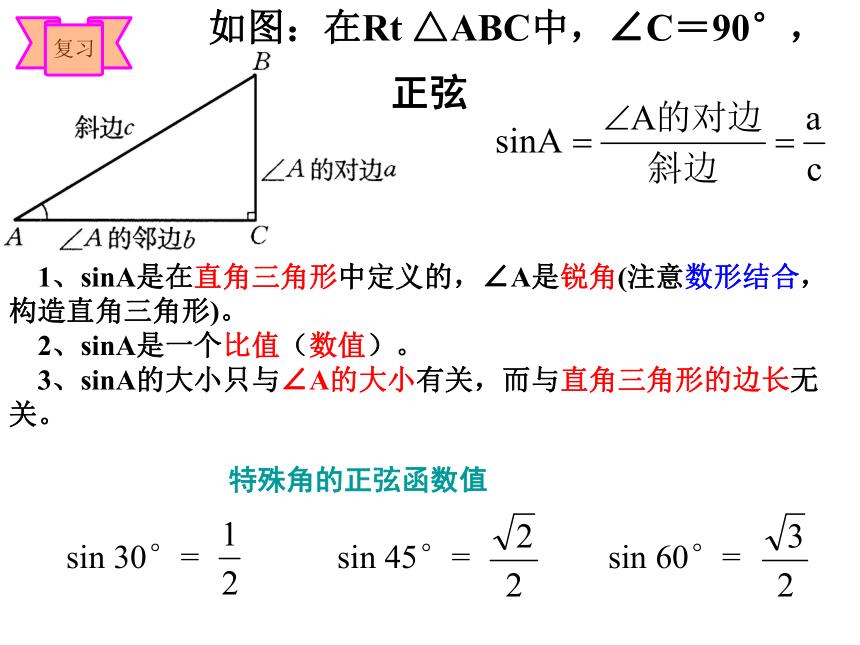
课件11张PPT。锐角三角函数(2)广水市城郊中心中学 1、sinA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2、sinA是一个比值(数值)。
3、sinA的大小只与∠A的大小有关,而与直角三角形的边长无关。如图:在Rt △ABC中,∠C=90°,sin 30°=sin 45°=sin 60°=特殊角的正弦函数值正弦 当直角三角形的一个锐角的大小确定时,其任意两边的比值都是惟一确定的吗?为什么?探究我们把∠A的邻边与斜边的比叫做∠A的余弦,
记作cosA,即把∠A的对边与邻边的比叫做∠A的正切,
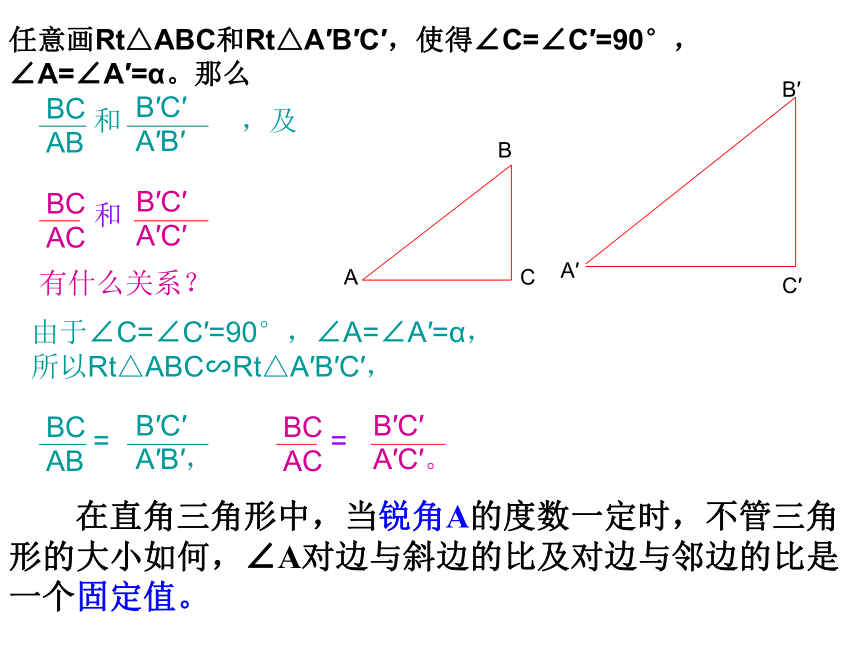
记作tanA,即 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A对边与斜边的比及对边与邻边的比是一个固定值。任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=α。那么有什么关系?,及由于∠C=∠C′=90°,∠A=∠A′=α,
所以Rt△ABC∽Rt△A′B′C′,如图:在Rt △ABC中,∠C=90°,∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c。邻边对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是A的函数,同样地,cosA,tanA也是A的函数。锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。例 如图,在Rt△ABC中,∠C=90°,BC=6,
sinA= ,求cosA,tanB的值。解:∵sinA= ,
∴AB= =6× =10,又 AC= = 8,∴cosA= ,tanB=应用举例1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。① a=9 b=12② a=9 b=12 2、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。 3、已知∠A为锐角,sinA= ,求cosA、tanA的值。4、如图,在Rt△ABC中,∠C=90°,AC=8,
tanA= ,求sinA,cosB的值。 1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定C试一试: 2、下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。BCADACBD在Rt△ABC中定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 再见
2、sinA是一个比值(数值)。
3、sinA的大小只与∠A的大小有关,而与直角三角形的边长无关。如图:在Rt △ABC中,∠C=90°,sin 30°=sin 45°=sin 60°=特殊角的正弦函数值正弦 当直角三角形的一个锐角的大小确定时,其任意两边的比值都是惟一确定的吗?为什么?探究我们把∠A的邻边与斜边的比叫做∠A的余弦,
记作cosA,即把∠A的对边与邻边的比叫做∠A的正切,
记作tanA,即 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A对边与斜边的比及对边与邻边的比是一个固定值。任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=α。那么有什么关系?,及由于∠C=∠C′=90°,∠A=∠A′=α,
所以Rt△ABC∽Rt△A′B′C′,如图:在Rt △ABC中,∠C=90°,∠A的对边记作a,
∠B的对边记作b,
∠C的对边记作c。邻边对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是A的函数,同样地,cosA,tanA也是A的函数。锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。例 如图,在Rt△ABC中,∠C=90°,BC=6,
sinA= ,求cosA,tanB的值。解:∵sinA= ,
∴AB= =6× =10,又 AC= = 8,∴cosA= ,tanB=应用举例1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。① a=9 b=12② a=9 b=12 2、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。 3、已知∠A为锐角,sinA= ,求cosA、tanA的值。4、如图,在Rt△ABC中,∠C=90°,AC=8,
tanA= ,求sinA,cosB的值。 1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定C试一试: 2、下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。BCADACBD在Rt△ABC中定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 再见
