24.1.2垂直于弦的直径课件
图片预览










文档简介
课件38张PPT。能记住圆是轴对称图形,并能正确说出圆的对称轴.
能记住垂径定理及推论,并能运用它们解决相关的证明、计算、作图等问题.24.1 圆的有关性质学习目标1第2课时 垂直于弦的直径什么是轴对称图形?
我们学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.回 顾线段角等腰三角形矩形菱形等腰梯形正方形互动课堂(探究与合作)探究点1:圆的对称性1.动手做一做: 剪一个圆形纸片,用对折的方法,在纸片上找出圆心O,并画出圆的任意一条直径CD,A是⊙O上任意一点(不与点C、D重合),过点A作AA1⊥CD,交⊙O于点A1,垂足为E,连接OA、OA1.3⑵在△OAA1中,∵OA=OA1,AA1⊥CD,∴AE=A1E.
即CD是AA1的 .这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A1,因此⊙O关于直线 对称.⑴在对折找圆心的过程中,我们发现:任意折痕(即
圆的直径所在的直线)两旁的部分 完全重合.4能够垂直平分线CD 圆是 图形,任何一条直径所在的
都是它的对称轴,圆有 条对称轴.轴对称直线无数2.通过上面的探究,你能得出结论:探究点2:垂径定理62.质疑1:若AB是直径,上述结论还成立么? 成立,当AB是直径时,OA=OB,CD⊥AB,所以CD是AB的垂直平分线,所以 = ,
= .⑵定理中的弦为直径时,结论仍然 .⑴垂径定理:垂直于弦的直径 弦,并且
平分弦所对的两条 .平分弧成立3.从上面的证明我们知道:注意:⑴垂径定理中的垂径可以是 、
半径或过圆心的直线或 ,其本
质是“过圆心”. ⑵垂径定理也可理
解为,如果一条直线,它具有两个性
质:①经过 ; ② 于弦.
那么这条直线就 这条弦, 弦
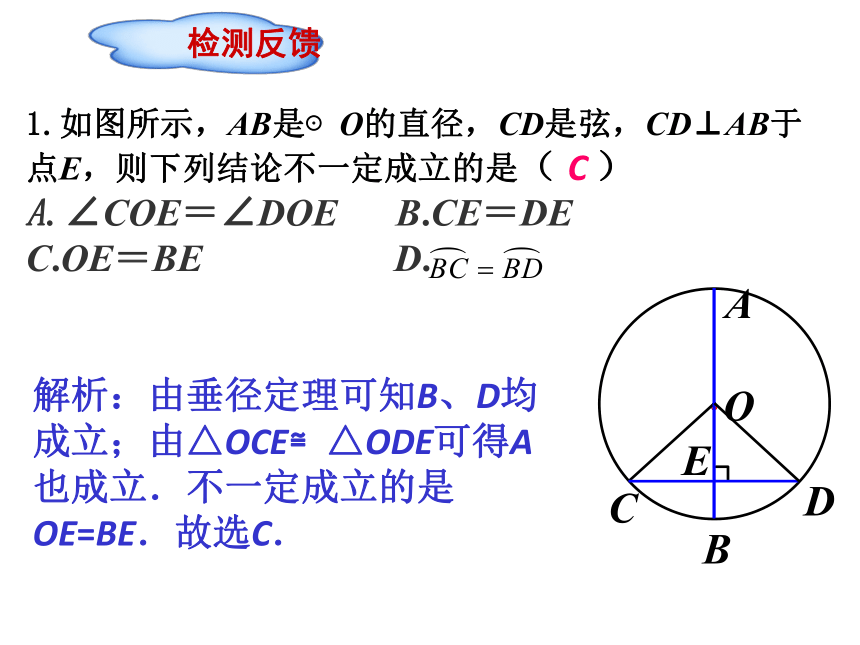
所对劣弧和优弧.7垂直直径线段圆心平分平分检测反馈解析:由垂径定理可知B、D均成立;由△OCE≌△ODE可得A也成立.不一定成立的是OE=BE.故选C.·OCDABE1.如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D. C探究点3 结论改为:②垂直于弦,④平分弦所对的劣弧,⑤平分弦所对的优弧.
这个命题正确吗?
1.垂径定理的条件和结论分别是什么?
条件:结论:③平分弦,④平分弦所对的劣弧,⑤平分弦所对的优弧.①过圆心,②垂直于弦.
质疑2.条件改为:①过圆心,③平分弦.
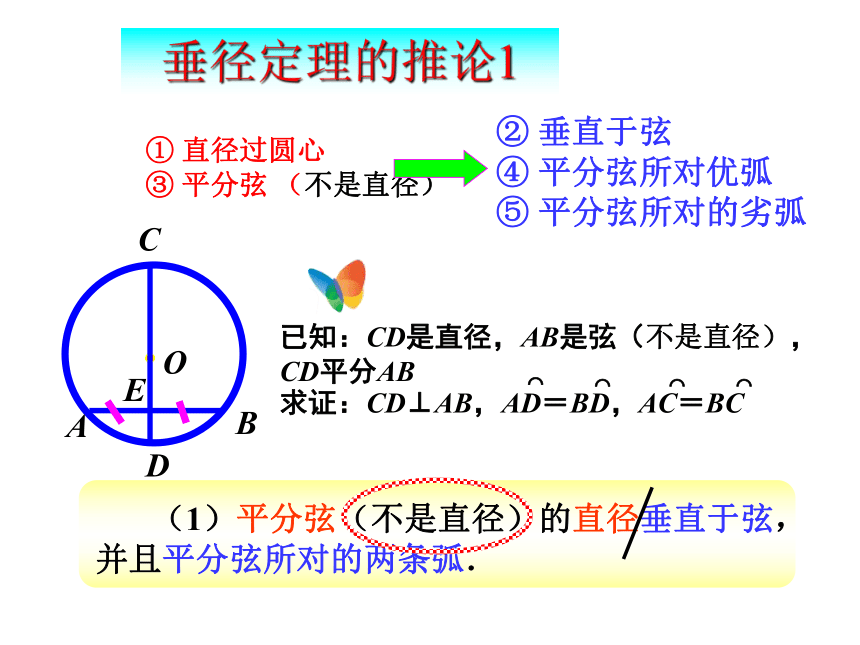
10探究点4:垂径定理的推论1.如图,在⊙O中,CD是直径,AB是弦(不是直径),AB、CD交于点E,且AE=BE,在⊙O中,连接OA、OB,则△OAB是 三角形,
∵AE=BE,
∴CD AB,即CD是垂直于弦的直径,
∴ , .⊥==等腰11质疑3:如果上图中的AB是直径,上述结论成立么? 不一定成立,如图所示,当AB是直径时,CD平分AB,但CD不垂直于AB,结论不成立.通过上面的证明,你能得出结论:⑴垂径定理的推论:平分弦(不是直径)的
直径 于弦,并且 弦所对的两条弧.垂直平分⑵垂径定理的推论中的弦一定要 为 ,否
则命题就不一定成立.非直径① 直径过圆心
③ 平分弦 (不是直径)② 垂直于弦
④ 平分弦所对优弧
⑤ 平分弦所对的劣弧 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论1① 直径过圆心
④ 平分弦所对优弧 ③ 平分弦
② 垂直于弦
⑤ 平分弦所对的劣弧垂径定理的推论1 (2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.② 垂直于弦
③ 平分弦 ① 直径过圆心
④ 平分弦所对优弧
⑤ 平分弦所对的劣弧 (3)弦的垂直平分线 经过圆心,并且平分弦所对的两条弧. 垂径定理的推论1② 垂直于弦
④ 平分弦所对优弧① 直径过圆心
③ 平分弦
⑤ 平分弦所对的劣弧推论1的其他命题......② 垂直于弦
⑤ 平分弦所对的劣弧① 直径过圆心
③ 平分弦
④ 平分弦所对优弧 (4)垂直于弦并且平分弦所对的一条弧的直径过圆心,并且平分弦和所对的另一条弧.③ 平分弦
④ 平分弦所对优弧① 直径过圆心
② 垂直于弦
⑤ 平分弦所对的劣弧 (5)平分弦并且平分弦所对的一条弧的直径过圆心,垂直于弦,并且平分弦所对的另一条弧 .③ 平分弦
⑤ 平分弦所对的劣弧① 直径过圆心
② 垂直于弦
④ 平分弦所对优弧④ 平分弦所对优弧
⑤ 平分弦所对的劣弧① 直径过圆心
② 垂直于弦
③ 平分弦 (6)平分弦所对的两条弧的直径过圆心,并且垂直平分弦.18归纳总结:综合以上探究可知: 如果一条直线具有:⑴经过 ;⑵垂直 ;⑶平分弦(被平分的弦不是 );⑷ 所对的优弧;⑸ 所对劣弧.这五条性质中的任意两条,那么必然具备其余三条性质.圆心于弦直径平分弦平分弦 平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.3.垂径定理的推论垂径定理的推论2圆的两条平行弦所夹的弧相等.MOABNCD证明:作直径MN垂直于弦AB∵ AB∥CD
∴ 直径MN也垂直于弦CD两条弦在圆心的同侧两条弦在圆心的两侧垂径定理的推论2有这两种情况:考考你探究案p147第6题垂径定理三角形d + h = rdhar有哪些等量关系? 在a,d,r,h中,已知其中任意两个量,可以求出其它两个量. 经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.4. 解决有关弦的问题1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
B解析:过O作OC⊥AB于C,∵OC过O,
∴AC=BC= AB=12,在Rt△AOC中,
由勾股定理得:
故选B. 2. 在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD.证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BDECDABE作法:1. 连结AB.小练习ABCDE作法:1. 连结AB.3. 连结AC.5. 点G同理.ABC作AC的垂直平分线作BC的垂直平分线这种方法对吗? 等分弧时一定要作弧所夹弦的垂直平分线.×你能破镜重圆吗?ABCmnO 作弦AB、AC及它们的垂直平分线m、n,交于O点;以O为圆心,OA为半径作圆.作法:依据: 弦的垂直平分线经过圆心,并且平分弦所对的两条弧. 你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.,拱高(弧的中点到弦的距离)为7.2m. 赵州桥主桥拱的半径是多少? 垂径定理的应用 用 表示主桥拱,设 所在圆的圆心为O,半径为R.
经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是 的中点,CD 就是拱高.解:AB=37.4,CD=7.2,OD=OC-CD=R-7.2解得 R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2 1. 判断:
(1)垂直于弦的直线平分这条弦,并且平分弦所对的两弧. ( )
(2)平分弦所对的一条弧的直径一定平分这条弦所对的另一弧. ( )
(3)经过弦的中点的直径一定垂直于弦. ( )
(4)圆的两条弦所夹的弧相等,则这两条弦平行.
( )
(5)弦的垂直平分线一定平分这条弦所对的弧.
( )√???√随堂练习2.如图所示,P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为______;最长弦长为______.8cm10cm解析:当弦与OP垂直时,弦最短,连接OA,由勾股定理可得,AP= =4,∵OP⊥AB,∴AB=2AP=8,最短弦为8cm.过P点经过圆心的弦最长为直径,最长弦为10cm.故填8cm,10cm.3.如图,AB是⊙O的弦,半径OC⊥AB于点D.
(1)若AB=8cm,OC=5cm,求CD的长;
(2)若OC=5cm,OD=3cm,求AB的长;
(3)若AB=8cm,CD=2cm,求⊙O的半径.(3)设⊙O的半径为r,则OD=r-2,∵OC⊥AB,∴AD= AB=4cm,在Rt△OAD中,OA2=DO2+AD2,∴r2=(r-2)2+42,解得r=5,∴⊙O的半径为5cm.解:连接OA,则AO=OC=5cm.∵OC⊥AB,∴∠ODA=90°.
(1) ∵OC⊥AB,∴AD= AB=4cm,在Rt△OAD中,
∴CD=OC-OD=2cm. (2)在Rt△OAD中,
∵OC⊥AB,AB=2AD=8cm. 4. 在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 5. 一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.
能记住垂径定理及推论,并能运用它们解决相关的证明、计算、作图等问题.24.1 圆的有关性质学习目标1第2课时 垂直于弦的直径什么是轴对称图形?
我们学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.回 顾线段角等腰三角形矩形菱形等腰梯形正方形互动课堂(探究与合作)探究点1:圆的对称性1.动手做一做: 剪一个圆形纸片,用对折的方法,在纸片上找出圆心O,并画出圆的任意一条直径CD,A是⊙O上任意一点(不与点C、D重合),过点A作AA1⊥CD,交⊙O于点A1,垂足为E,连接OA、OA1.3⑵在△OAA1中,∵OA=OA1,AA1⊥CD,∴AE=A1E.
即CD是AA1的 .这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A1,因此⊙O关于直线 对称.⑴在对折找圆心的过程中,我们发现:任意折痕(即
圆的直径所在的直线)两旁的部分 完全重合.4能够垂直平分线CD 圆是 图形,任何一条直径所在的
都是它的对称轴,圆有 条对称轴.轴对称直线无数2.通过上面的探究,你能得出结论:探究点2:垂径定理62.质疑1:若AB是直径,上述结论还成立么? 成立,当AB是直径时,OA=OB,CD⊥AB,所以CD是AB的垂直平分线,所以 = ,
= .⑵定理中的弦为直径时,结论仍然 .⑴垂径定理:垂直于弦的直径 弦,并且
平分弦所对的两条 .平分弧成立3.从上面的证明我们知道:注意:⑴垂径定理中的垂径可以是 、
半径或过圆心的直线或 ,其本
质是“过圆心”. ⑵垂径定理也可理
解为,如果一条直线,它具有两个性
质:①经过 ; ② 于弦.
那么这条直线就 这条弦, 弦
所对劣弧和优弧.7垂直直径线段圆心平分平分检测反馈解析:由垂径定理可知B、D均成立;由△OCE≌△ODE可得A也成立.不一定成立的是OE=BE.故选C.·OCDABE1.如图所示,AB是⊙O的直径,CD是弦,CD⊥AB于点E,则下列结论不一定成立的是( )
A.∠COE=∠DOE B.CE=DE
C.OE=BE D. C探究点3 结论改为:②垂直于弦,④平分弦所对的劣弧,⑤平分弦所对的优弧.
这个命题正确吗?
1.垂径定理的条件和结论分别是什么?
条件:结论:③平分弦,④平分弦所对的劣弧,⑤平分弦所对的优弧.①过圆心,②垂直于弦.
质疑2.条件改为:①过圆心,③平分弦.
10探究点4:垂径定理的推论1.如图,在⊙O中,CD是直径,AB是弦(不是直径),AB、CD交于点E,且AE=BE,在⊙O中,连接OA、OB,则△OAB是 三角形,
∵AE=BE,
∴CD AB,即CD是垂直于弦的直径,
∴ , .⊥==等腰11质疑3:如果上图中的AB是直径,上述结论成立么? 不一定成立,如图所示,当AB是直径时,CD平分AB,但CD不垂直于AB,结论不成立.通过上面的证明,你能得出结论:⑴垂径定理的推论:平分弦(不是直径)的
直径 于弦,并且 弦所对的两条弧.垂直平分⑵垂径定理的推论中的弦一定要 为 ,否
则命题就不一定成立.非直径① 直径过圆心
③ 平分弦 (不是直径)② 垂直于弦
④ 平分弦所对优弧
⑤ 平分弦所对的劣弧 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论1① 直径过圆心
④ 平分弦所对优弧 ③ 平分弦
② 垂直于弦
⑤ 平分弦所对的劣弧垂径定理的推论1 (2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.② 垂直于弦
③ 平分弦 ① 直径过圆心
④ 平分弦所对优弧
⑤ 平分弦所对的劣弧 (3)弦的垂直平分线 经过圆心,并且平分弦所对的两条弧. 垂径定理的推论1② 垂直于弦
④ 平分弦所对优弧① 直径过圆心
③ 平分弦
⑤ 平分弦所对的劣弧推论1的其他命题......② 垂直于弦
⑤ 平分弦所对的劣弧① 直径过圆心
③ 平分弦
④ 平分弦所对优弧 (4)垂直于弦并且平分弦所对的一条弧的直径过圆心,并且平分弦和所对的另一条弧.③ 平分弦
④ 平分弦所对优弧① 直径过圆心
② 垂直于弦
⑤ 平分弦所对的劣弧 (5)平分弦并且平分弦所对的一条弧的直径过圆心,垂直于弦,并且平分弦所对的另一条弧 .③ 平分弦
⑤ 平分弦所对的劣弧① 直径过圆心
② 垂直于弦
④ 平分弦所对优弧④ 平分弦所对优弧
⑤ 平分弦所对的劣弧① 直径过圆心
② 垂直于弦
③ 平分弦 (6)平分弦所对的两条弧的直径过圆心,并且垂直平分弦.18归纳总结:综合以上探究可知: 如果一条直线具有:⑴经过 ;⑵垂直 ;⑶平分弦(被平分的弦不是 );⑷ 所对的优弧;⑸ 所对劣弧.这五条性质中的任意两条,那么必然具备其余三条性质.圆心于弦直径平分弦平分弦 平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.3.垂径定理的推论垂径定理的推论2圆的两条平行弦所夹的弧相等.MOABNCD证明:作直径MN垂直于弦AB∵ AB∥CD
∴ 直径MN也垂直于弦CD两条弦在圆心的同侧两条弦在圆心的两侧垂径定理的推论2有这两种情况:考考你探究案p147第6题垂径定理三角形d + h = rdhar有哪些等量关系? 在a,d,r,h中,已知其中任意两个量,可以求出其它两个量. 经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件.4. 解决有关弦的问题1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
B解析:过O作OC⊥AB于C,∵OC过O,
∴AC=BC= AB=12,在Rt△AOC中,
由勾股定理得:
故选B. 2. 在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD.证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
AE-CE=BE-DE.
所以,AC=BDECDABE作法:1. 连结AB.小练习ABCDE作法:1. 连结AB.3. 连结AC.5. 点G同理.ABC作AC的垂直平分线作BC的垂直平分线这种方法对吗? 等分弧时一定要作弧所夹弦的垂直平分线.×你能破镜重圆吗?ABCmnO 作弦AB、AC及它们的垂直平分线m、n,交于O点;以O为圆心,OA为半径作圆.作法:依据: 弦的垂直平分线经过圆心,并且平分弦所对的两条弧. 你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.,拱高(弧的中点到弦的距离)为7.2m. 赵州桥主桥拱的半径是多少? 垂径定理的应用 用 表示主桥拱,设 所在圆的圆心为O,半径为R.
经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是 的中点,CD 就是拱高.解:AB=37.4,CD=7.2,OD=OC-CD=R-7.2解得 R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2 1. 判断:
(1)垂直于弦的直线平分这条弦,并且平分弦所对的两弧. ( )
(2)平分弦所对的一条弧的直径一定平分这条弦所对的另一弧. ( )
(3)经过弦的中点的直径一定垂直于弦. ( )
(4)圆的两条弦所夹的弧相等,则这两条弦平行.
( )
(5)弦的垂直平分线一定平分这条弦所对的弧.
( )√???√随堂练习2.如图所示,P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为______;最长弦长为______.8cm10cm解析:当弦与OP垂直时,弦最短,连接OA,由勾股定理可得,AP= =4,∵OP⊥AB,∴AB=2AP=8,最短弦为8cm.过P点经过圆心的弦最长为直径,最长弦为10cm.故填8cm,10cm.3.如图,AB是⊙O的弦,半径OC⊥AB于点D.
(1)若AB=8cm,OC=5cm,求CD的长;
(2)若OC=5cm,OD=3cm,求AB的长;
(3)若AB=8cm,CD=2cm,求⊙O的半径.(3)设⊙O的半径为r,则OD=r-2,∵OC⊥AB,∴AD= AB=4cm,在Rt△OAD中,OA2=DO2+AD2,∴r2=(r-2)2+42,解得r=5,∴⊙O的半径为5cm.解:连接OA,则AO=OC=5cm.∵OC⊥AB,∴∠ODA=90°.
(1) ∵OC⊥AB,∴AD= AB=4cm,在Rt△OAD中,
∴CD=OC-OD=2cm. (2)在Rt△OAD中,
∵OC⊥AB,AB=2AD=8cm. 4. 在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形. 5. 一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.
同课章节目录
