九年级上23.1.1图形的旋转课件

(共14张PPT)
人教版九年级数学上册第二十三章
23.1.1
(1)上面的转动现象，有什么共同的特征？
(2)钟表的指针、秋千、车轮在转动过程中，其形状、大小、位置是否发生变化呢？
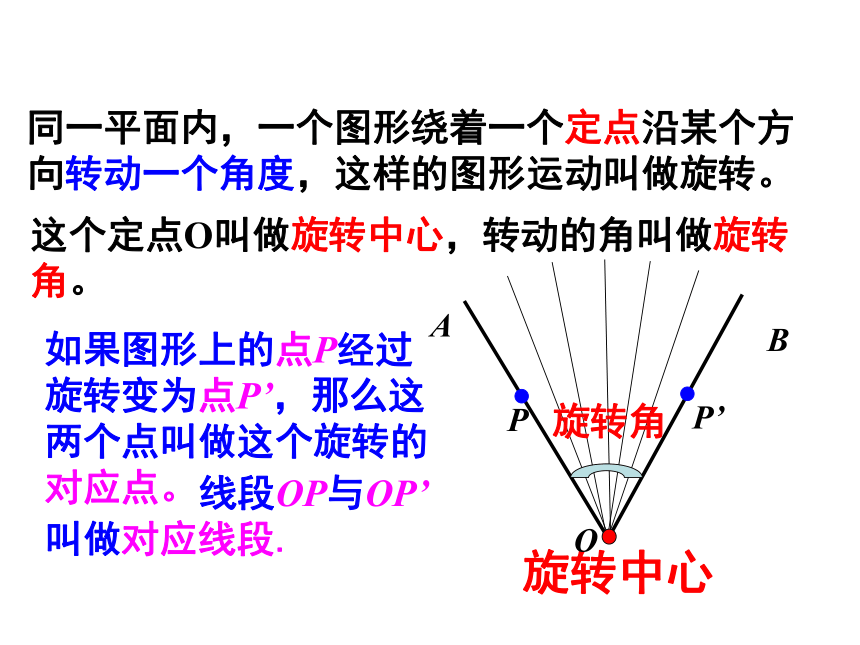
这个定点O叫做旋转中心，转动的角叫做旋转角。
旋转角
旋转中心
同一平面内，一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动叫做旋转。
A
O
B
P
P’
如果图形上的点P经过旋转变为点P’，那么这两个点叫做这个旋转的对应点。
线段OP与OP’叫做对应线段.
B
O
A
45
0
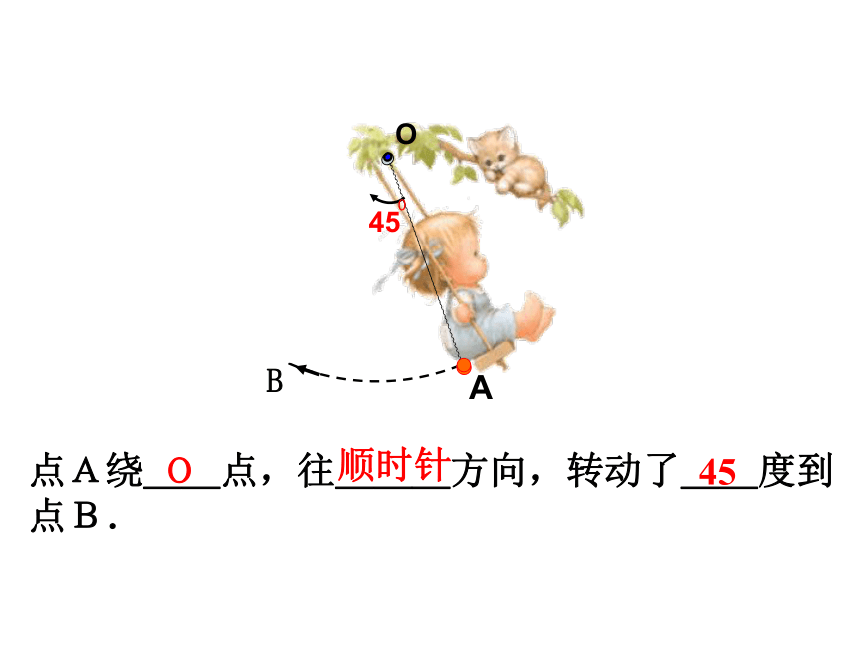
点Ａ绕＿＿点，往＿＿＿方向，转动了＿＿度到点Ｂ．
Ｏ
顺时针
45
P
B
A
B
/
A
/
90
0
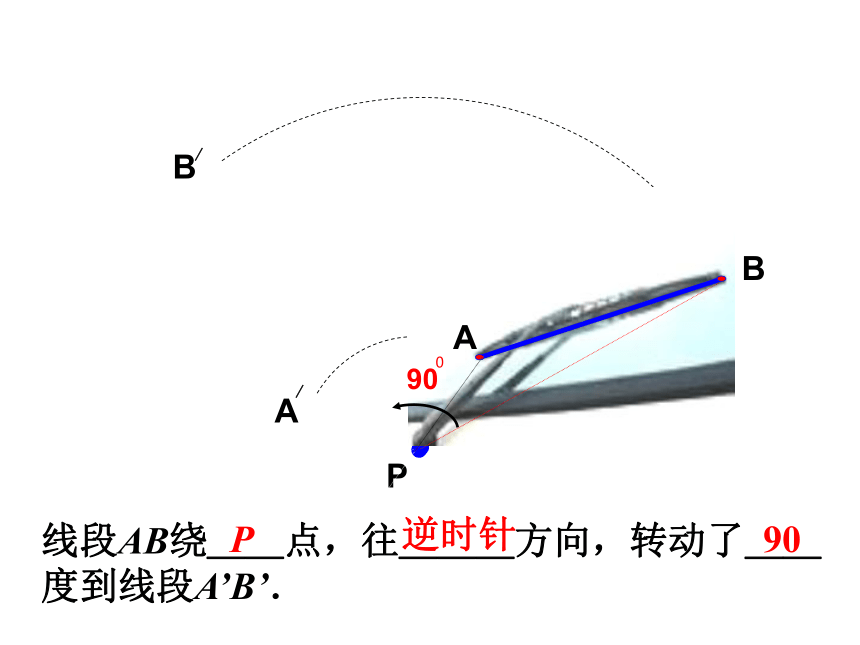
线段AB绕＿＿点，往＿＿＿方向，转动了＿＿度到线段A’B’．
P
逆时针
90
B
A
B
A
C
C
O
100
0
旋转中心
旋转角度
旋转方向
旋转的三要素:
△ABC绕＿＿点，往＿＿＿方向，转动了＿＿度到△A’B’C’ ．
Ｏ
顺时针
100
B
A
B
A
C
C
O
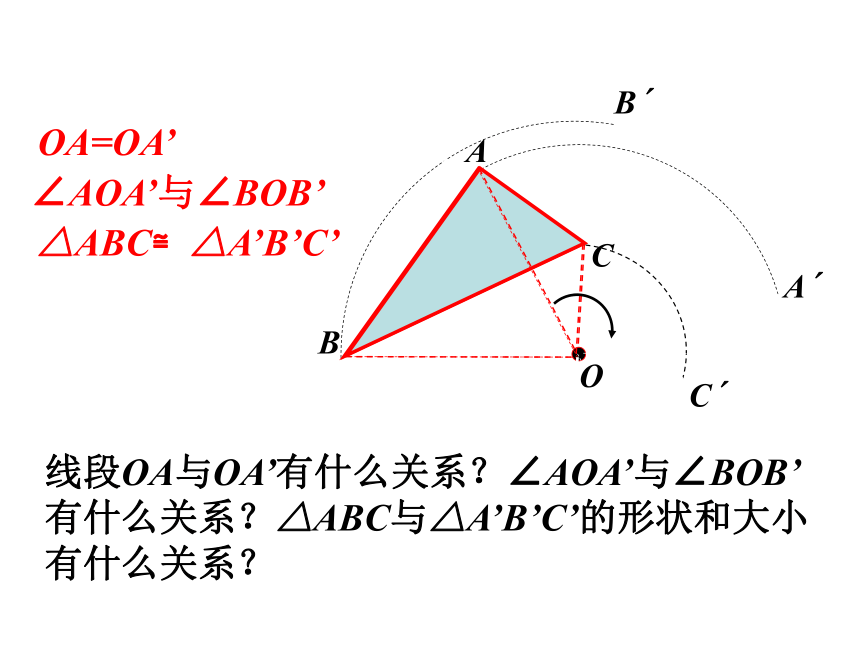
线段OA与OA’有什么关系？∠AOA’与∠BOB’有什么关系？△ABC与△A’B’C’的形状和大小有什么关系？
OA=OA’
∠AOA’与∠BOB’
△ABC≌△A’B’C’
B
A
B
A
C
C
O
OA=OA’
∠AOA’与∠BOB’
△ABC≌△A’B’C’
对应点到旋转中心的距离相等.
对应点与旋转中心所连线段的夹角等于旋转角.
旋转前后的图形全等.
B
A
C
D
例 如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.
E
E’
归纳与小结
1.旋转的相关概念.
2.旋转的性质.
A
B
O
C
D
点A的对应点是________;
旋转中心是________;
旋转角是_________________;
1.如图,△ABO绕点O旋转得到△CDO,则:
点C
点O
∠AOC,
∠BOD
B
A
E
D
C
F
M
2.如图,△ABC绕点M旋转得到△ DEF,则:
点Ｃ的对应点是________;
旋转中心是________;
旋转角是______________________;
点F
点M
∠AMD，
∠BME，
∠CMF
旋转方向是________;
顺时针
课 后
作 业
1. 《全品作业》相关内容.
2. 《同步练习册》相关内容.