高一物理人教版必修1(第3.2 弹力 课时同步附解析
文档属性
| 名称 | 高一物理人教版必修1(第3.2 弹力 课时同步附解析 |  | |
| 格式 | zip | ||
| 文件大小 | 109.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-11-29 19:08:25 | ||
图片预览


文档简介
绝密★启用前
人教版必修1
第三章相互作用
2.弹力
第Ⅰ部分选择题
一、选择题:本题共8小题。将正确答案填写在题干后面的括号里。
1.关于弹力,下列说法不正确的是( )
A.书对桌面压力的方向垂直于桌面
B.书对桌面的压力和桌面对书的支持力都是弹力
C.在弹性限度内,弹簧弹力的大小与弹簧的长度成正比
D.在弹性限度内,弹簧弹力的大小与弹簧的伸长量成正比
2.杂技演员有高超的技术,能轻松地顶接从高处落下的坛子,关于他顶坛时头顶受到的压力,产生的直接原因是( )
A.坛的形变
B.头的形变
C.物体受到的重力
D.人受到的重力
3.下列说法中不正确的是( )
A.书放在水平桌面上受到的支持力,是由于书发生了微小形变而产生的
B.用细木棍拨动浮在水中的圆木,圆木受到的弹力是由于细木棍发生形变而产生的
C.绳对物体的拉力方向总是沿着绳而指向绳收缩的方向
D.支持力的方向总是垂直于支持面而指向被支持的物体
4.篮球放在光滑水平地面上与竖直墙面相靠,且处于静止状态,则篮球的受力情况是( )
A.受重力、水平面的支持力和墙面的弹力
B.受重力、水平面的支持力和篮球对地面的压力
C.受重力和篮球对地面的压力
D.受重力和水平面的支持力
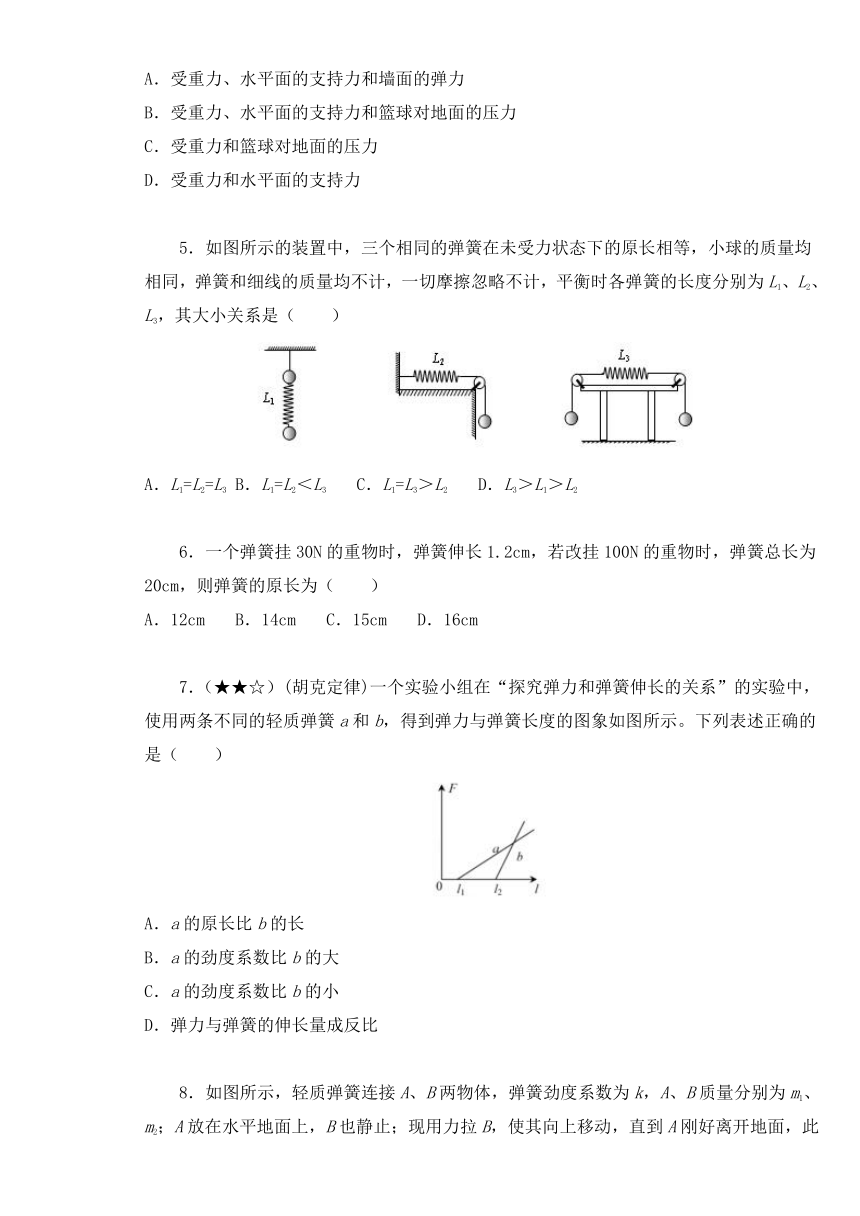
5.如图所示的装置中,三个相同的弹簧在未受力状态下的原长相等,小球的质量均相同,弹簧和细线的质量均不计,一切摩擦忽略不计,平衡时各弹簧的长度分别为L1、L2、L3,其大小关系是( )
A.L1=L2=L3
B.L1=L2<L3
C.L1=L3>L2
D.L3>L1>L2
6.一个弹簧挂30N的重物时,弹簧伸长1.2cm,若改挂100N的重物时,弹簧总长为20cm,则弹簧的原长为( )
A.12cm
B.14cm
C.15cm
D.16cm
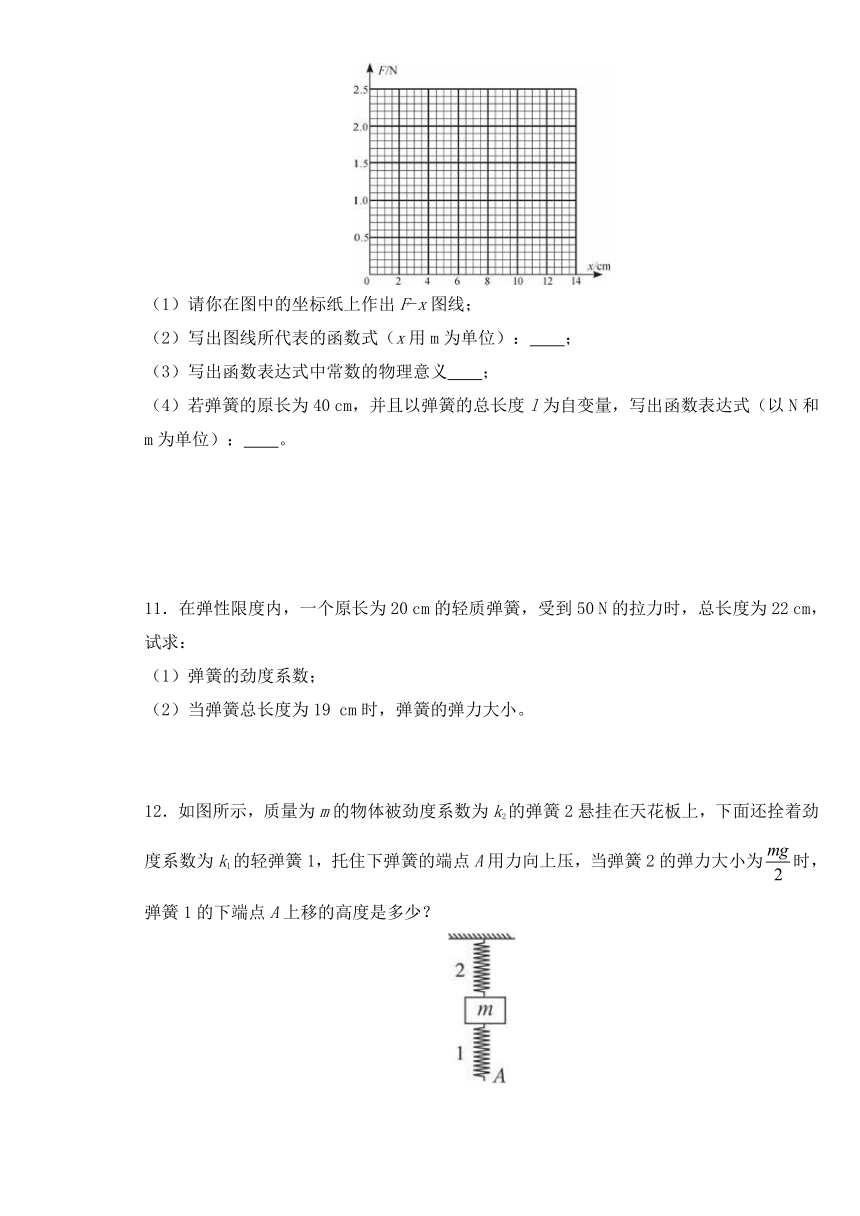
7.(★★☆)(胡克定律)一个实验小组在“探究弹力和弹簧伸长的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图所示。下列表述正确的是( )
A.a的原长比b的长
B.a的劲度系数比b的大
C.a的劲度系数比b的小
D.弹力与弹簧的伸长量成反比
8.如图所示,轻质弹簧连接A、B两物体,弹簧劲度系数为k,A、B质量分别为m1、m2;A放在水平地面上,B也静止;现用力拉B,使其向上移动,直到A刚好离开地面,此过程中,B物体向上移动的距离为( )
A.
B.
C.
D.
第Ⅱ部分非选择题
二、非选择题:本题4个小题。将符合题意的内容填写在题目中的横线上,或按题目要求作答。解答应写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分;有数值计算的题,答案中必须明确写出数值和单位。
9.在弹性限度之内,一轻弹簧受到10
N的拉力时,它的伸长量是4
cm,则该弹簧劲度系数是 N/m,当弹簧不受拉力时,该弹簧劲度系数是
N/m,当弹簧两端受到拉力为10
N,弹簧的伸长量是 cm。
10.下表是某同学为“探究弹力与弹簧伸长量的关系”所测的几组数据:
(1)请你在图中的坐标纸上作出F-x图线;
(2)写出图线所代表的函数式(x用m为单位): ;
(3)写出函数表达式中常数的物理意义 ;
(4)若弹簧的原长为40
cm,并且以弹簧的总长度l为自变量,写出函数表达式(以N和m为单位): 。
11.在弹性限度内,一个原长为20
cm的轻质弹簧,受到50
N的拉力时,总长度为22
cm,试求:
(1)弹簧的劲度系数;
(2)当弹簧总长度为19
cm时,弹簧的弹力大小。
12.如图所示,质量为m的物体被劲度系数为k2的弹簧2悬挂在天花板上,下面还拴着劲度系数为k1的轻弹簧1,托住下弹簧的端点A用力向上压,当弹簧2的弹力大小为时,弹簧1的下端点A上移的高度是多少?
人教版必修1
第三章相互作用
2.弹力
参考答案及解析
一、选择题
【答案】
1.C
【解析】弹力的方向垂直于接触面,所以书对桌面压力的方向垂直于桌面,故A不符合题意;压力和支持力都属于弹力,故B不符合题意;根据胡克定律F=kx,其中x为弹簧的形变量,而不是弹簧的长度,
D不符合题意,故本题选
C。
【答案】
2.A
【解析】头顶受到的压力是由于坛子产生形变,对与之接触的头产生力的作用,选项A正确,B、C、D错误。
【答案】
3.A
【解析】书受到的支持力,是由于桌面发生了微小形变而产生的,故A错误;圆木受到的弹力是由于木棍发生形变产生的,故B正确;绳的拉力与绳子形变量方向相反,故C正确;由支持力的概念可知,支持力的方向总是垂直于支持面而指向被支持的物体,故D正确。
【答案】
4.D
【解析】篮球受重力作用,要与地面接触并发生挤压,因此受到水平面的支持力,假设篮球受到竖直墙面的弹力,因为水平地面光滑,所以篮球不受面的摩擦力,水平方向不满足二力平衡,篮球不可能静止,假设不成立,即篮球不受竖直墙面的弹力,故选项D正确。
【答案】
5.A
【解析】以小球或下面小球为研究对象,由平衡条件得知,弹簧的弹力等于小球的重力G,由胡克定律F=kx(x是指弹簧的伸长量或压缩量)知,三个图中弹簧的形变量相同,故L1=L2=L3。选项A正确。
【答案】
6.D
【解析】一个弹簧挂30N的重物时,弹簧伸长1.2cm,根据胡克定律,有:F1=kx1;得k==
N/m
=2
500
N/m;若挂100N的重物时,有:F2=kx2;解得x2=m=0.04
m=4
cm,故弹簧的原长为:x0=x-x2=20cm-4cm=16cm。
【答案】
7.C
【解析】弹簧的弹力满足胡克定律,F=k(l-l0),在图象中横截距表示弹簧的原长,故b的原长比a的长,故A错误;在图象中斜率表示弹簧的劲度系数k,故a的劲度系数比b的小,故B错误,C正确;弹力与弹簧的形变量成正比,故D错误。
【答案】
8.C
【解析】开始时,A、B都处于静止状态,弹簧的压缩量设为x1,由胡克定律有kx1=m2g,
物体A恰好离开地面时,弹簧的拉力为m1g,设此时弹簧的伸长量为x2,由胡克定律有kx2=m1g,这一过程中,物体B上移的距离x=x1+x2=,故选C。
二、非选择题
【答案】
9.
250
250
4
【解析】根据胡克定律F=kΔx得,k==
N/m
=250
N/m;
弹簧的劲度系数由弹簧本身决定与受不受力无关,故为250
N/m;
当弹簧两端受到拉力为10
N,弹簧的拉力为10
N,则x′==m=0.04
m=4
cm。
【答案】
10.
(1)如图(2)F=20x(3)该弹簧每伸长(或压缩)1
m,其弹力增加20
N,即为弹簧的劲度系数(4)F=20(l-0.4)
【解析】(1)将x轴每一小格取为0.51cm,F轴每一小格取为0.1N,将各点描到坐标纸上,并连成直线
(2)由图象得直线的斜率k=0.2,如果x用m为单位,所以函数式为F=20x;
(3)函数表达式中常数的物理意义表示该弹簧每伸长(或压缩)1
m,其弹力增加20
N,即为弹簧的劲度系数;
(4)若弹簧的原长为40
cm,并且以弹簧的总长度l为自变量,函数表达式为:F=20x=
20(l-0.4)。
【答案】
11.
(1)2
500
N/m
(2)25
N
【解析】(1)根据胡克定律得:F=k
x
解得:k==2
500
N/m
(2)当弹簧总长度为19
cm时,根据胡克定律得F2=k(L0-L2)=25
N
【答案】
12.
或
【解析】A点上升的高度等于弹簧2和1缩短的长度之和,弹簧2可能处于拉伸状态也可能处于压缩状态
(1)A点上升,使弹簧2可能仍处于伸长状态时,弹力减小了
弹簧2比原来缩短:Δx2=
弹簧1的弹力为,压缩量为:Δx1=
所以A上移的高度是:Δx=Δx1+Δx2=
(2)A点上升,使弹簧2可能处于压缩状态时,向下的弹力
压缩量Δx2=,所以弹簧2上升的高度为:Δx′=
+Δx2=
弹簧1上的弹力为:mg+,弹簧1的形变量为:Δx1=
所以A上移的高度是:Δx=Δx1+Δx′=
所以弹簧1的下端点A上移的高度是或
人教版必修1
第三章相互作用
2.弹力
第Ⅰ部分选择题
一、选择题:本题共8小题。将正确答案填写在题干后面的括号里。
1.关于弹力,下列说法不正确的是( )
A.书对桌面压力的方向垂直于桌面
B.书对桌面的压力和桌面对书的支持力都是弹力
C.在弹性限度内,弹簧弹力的大小与弹簧的长度成正比
D.在弹性限度内,弹簧弹力的大小与弹簧的伸长量成正比
2.杂技演员有高超的技术,能轻松地顶接从高处落下的坛子,关于他顶坛时头顶受到的压力,产生的直接原因是( )
A.坛的形变
B.头的形变
C.物体受到的重力
D.人受到的重力
3.下列说法中不正确的是( )
A.书放在水平桌面上受到的支持力,是由于书发生了微小形变而产生的
B.用细木棍拨动浮在水中的圆木,圆木受到的弹力是由于细木棍发生形变而产生的
C.绳对物体的拉力方向总是沿着绳而指向绳收缩的方向
D.支持力的方向总是垂直于支持面而指向被支持的物体
4.篮球放在光滑水平地面上与竖直墙面相靠,且处于静止状态,则篮球的受力情况是( )
A.受重力、水平面的支持力和墙面的弹力
B.受重力、水平面的支持力和篮球对地面的压力
C.受重力和篮球对地面的压力
D.受重力和水平面的支持力
5.如图所示的装置中,三个相同的弹簧在未受力状态下的原长相等,小球的质量均相同,弹簧和细线的质量均不计,一切摩擦忽略不计,平衡时各弹簧的长度分别为L1、L2、L3,其大小关系是( )
A.L1=L2=L3
B.L1=L2<L3
C.L1=L3>L2
D.L3>L1>L2
6.一个弹簧挂30N的重物时,弹簧伸长1.2cm,若改挂100N的重物时,弹簧总长为20cm,则弹簧的原长为( )
A.12cm
B.14cm
C.15cm
D.16cm
7.(★★☆)(胡克定律)一个实验小组在“探究弹力和弹簧伸长的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图所示。下列表述正确的是( )
A.a的原长比b的长
B.a的劲度系数比b的大
C.a的劲度系数比b的小
D.弹力与弹簧的伸长量成反比
8.如图所示,轻质弹簧连接A、B两物体,弹簧劲度系数为k,A、B质量分别为m1、m2;A放在水平地面上,B也静止;现用力拉B,使其向上移动,直到A刚好离开地面,此过程中,B物体向上移动的距离为( )
A.
B.
C.
D.
第Ⅱ部分非选择题
二、非选择题:本题4个小题。将符合题意的内容填写在题目中的横线上,或按题目要求作答。解答应写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分;有数值计算的题,答案中必须明确写出数值和单位。
9.在弹性限度之内,一轻弹簧受到10
N的拉力时,它的伸长量是4
cm,则该弹簧劲度系数是 N/m,当弹簧不受拉力时,该弹簧劲度系数是
N/m,当弹簧两端受到拉力为10
N,弹簧的伸长量是 cm。
10.下表是某同学为“探究弹力与弹簧伸长量的关系”所测的几组数据:
(1)请你在图中的坐标纸上作出F-x图线;
(2)写出图线所代表的函数式(x用m为单位): ;
(3)写出函数表达式中常数的物理意义 ;
(4)若弹簧的原长为40
cm,并且以弹簧的总长度l为自变量,写出函数表达式(以N和m为单位): 。
11.在弹性限度内,一个原长为20
cm的轻质弹簧,受到50
N的拉力时,总长度为22
cm,试求:
(1)弹簧的劲度系数;
(2)当弹簧总长度为19
cm时,弹簧的弹力大小。
12.如图所示,质量为m的物体被劲度系数为k2的弹簧2悬挂在天花板上,下面还拴着劲度系数为k1的轻弹簧1,托住下弹簧的端点A用力向上压,当弹簧2的弹力大小为时,弹簧1的下端点A上移的高度是多少?
人教版必修1
第三章相互作用
2.弹力
参考答案及解析
一、选择题
【答案】
1.C
【解析】弹力的方向垂直于接触面,所以书对桌面压力的方向垂直于桌面,故A不符合题意;压力和支持力都属于弹力,故B不符合题意;根据胡克定律F=kx,其中x为弹簧的形变量,而不是弹簧的长度,
D不符合题意,故本题选
C。
【答案】
2.A
【解析】头顶受到的压力是由于坛子产生形变,对与之接触的头产生力的作用,选项A正确,B、C、D错误。
【答案】
3.A
【解析】书受到的支持力,是由于桌面发生了微小形变而产生的,故A错误;圆木受到的弹力是由于木棍发生形变产生的,故B正确;绳的拉力与绳子形变量方向相反,故C正确;由支持力的概念可知,支持力的方向总是垂直于支持面而指向被支持的物体,故D正确。
【答案】
4.D
【解析】篮球受重力作用,要与地面接触并发生挤压,因此受到水平面的支持力,假设篮球受到竖直墙面的弹力,因为水平地面光滑,所以篮球不受面的摩擦力,水平方向不满足二力平衡,篮球不可能静止,假设不成立,即篮球不受竖直墙面的弹力,故选项D正确。
【答案】
5.A
【解析】以小球或下面小球为研究对象,由平衡条件得知,弹簧的弹力等于小球的重力G,由胡克定律F=kx(x是指弹簧的伸长量或压缩量)知,三个图中弹簧的形变量相同,故L1=L2=L3。选项A正确。
【答案】
6.D
【解析】一个弹簧挂30N的重物时,弹簧伸长1.2cm,根据胡克定律,有:F1=kx1;得k==
N/m
=2
500
N/m;若挂100N的重物时,有:F2=kx2;解得x2=m=0.04
m=4
cm,故弹簧的原长为:x0=x-x2=20cm-4cm=16cm。
【答案】
7.C
【解析】弹簧的弹力满足胡克定律,F=k(l-l0),在图象中横截距表示弹簧的原长,故b的原长比a的长,故A错误;在图象中斜率表示弹簧的劲度系数k,故a的劲度系数比b的小,故B错误,C正确;弹力与弹簧的形变量成正比,故D错误。
【答案】
8.C
【解析】开始时,A、B都处于静止状态,弹簧的压缩量设为x1,由胡克定律有kx1=m2g,
物体A恰好离开地面时,弹簧的拉力为m1g,设此时弹簧的伸长量为x2,由胡克定律有kx2=m1g,这一过程中,物体B上移的距离x=x1+x2=,故选C。
二、非选择题
【答案】
9.
250
250
4
【解析】根据胡克定律F=kΔx得,k==
N/m
=250
N/m;
弹簧的劲度系数由弹簧本身决定与受不受力无关,故为250
N/m;
当弹簧两端受到拉力为10
N,弹簧的拉力为10
N,则x′==m=0.04
m=4
cm。
【答案】
10.
(1)如图(2)F=20x(3)该弹簧每伸长(或压缩)1
m,其弹力增加20
N,即为弹簧的劲度系数(4)F=20(l-0.4)
【解析】(1)将x轴每一小格取为0.51cm,F轴每一小格取为0.1N,将各点描到坐标纸上,并连成直线
(2)由图象得直线的斜率k=0.2,如果x用m为单位,所以函数式为F=20x;
(3)函数表达式中常数的物理意义表示该弹簧每伸长(或压缩)1
m,其弹力增加20
N,即为弹簧的劲度系数;
(4)若弹簧的原长为40
cm,并且以弹簧的总长度l为自变量,函数表达式为:F=20x=
20(l-0.4)。
【答案】
11.
(1)2
500
N/m
(2)25
N
【解析】(1)根据胡克定律得:F=k
x
解得:k==2
500
N/m
(2)当弹簧总长度为19
cm时,根据胡克定律得F2=k(L0-L2)=25
N
【答案】
12.
或
【解析】A点上升的高度等于弹簧2和1缩短的长度之和,弹簧2可能处于拉伸状态也可能处于压缩状态
(1)A点上升,使弹簧2可能仍处于伸长状态时,弹力减小了
弹簧2比原来缩短:Δx2=
弹簧1的弹力为,压缩量为:Δx1=
所以A上移的高度是:Δx=Δx1+Δx2=
(2)A点上升,使弹簧2可能处于压缩状态时,向下的弹力
压缩量Δx2=,所以弹簧2上升的高度为:Δx′=
+Δx2=
弹簧1上的弹力为:mg+,弹簧1的形变量为:Δx1=
所以A上移的高度是:Δx=Δx1+Δx′=
所以弹簧1的下端点A上移的高度是或
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
