第三章 函数的应用单元综合检测题三(带解析)
文档属性
| 名称 | 第三章 函数的应用单元综合检测题三(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 758.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-30 09:05:10 | ||
图片预览


文档简介
第三章 函数的应用单元综合检测题三(带解析)
一、选择题
1.已知函数f(x)=|log3x|,若a≠b时,有f(a)=f(b),则( )
A.a<b<1 B.a>b>1 C.ab=3 D.ab=1
2.若f(x)=|x2-2x-3|,则方程f3(x)-4f2(x)-f(x)+4=0的根的个数为( )
A.5 B.6 C.7 D.9
3.因工作人员不慎将63枚真纪念币和一枚假纪念币混在了一起,从其外形无法分辨,仅仅知道假纪念币的重量要比真纪念币稍稍轻一点点,现用一台天平,通过比较重量的方法来找出那枚假纪念币,则最多只需称量( )次.2-1-c-n-j-y
A.4 B.5 C.6 D.7
4.已知f(x)唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下面命题错误的( )
A.函数f(x)在(1,2)或[2,3)内有零点 B.函数f(x)在(3,5)内无零点 C.函数f(x)在(2,5)内有零点 D.函数f(x)在(2,4)内不一定有零点21*cnjy*com
5.用二分法求方程的近似根,精确度为e,则循环结构的终止条件是( )
A.|x1-x2|>e B.x1=x2=e C.|x1-x2|<e D.x1<e<x22·1·c·n·j·y
6.对实数a与b,定义新运算“?”:设函数f(x)=(x2-2)?(x-x2),x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A. B. C. D.
7.下列说法正确的是( )
A.函数y=f(x)的图象与直线x=a可能有两个交点
B.函数y=log2x2与函数y=2log2x是同一函数
C.对于[a,b]上的函数y=f(x),若有f(a)?f(b)<0,那么函数y=f(x)在(a,b)内有零点【来源:21cnj*y.co*m】
D.对于指数函数y=ax(a>1)与幂函数y=xn(n>0),总存在一个x,当x>x时,就会有ax>xn
8.在计算机的算法语言中有一种函数[x]叫做高斯函数,它表示数x的整数部分(即小于等于x的最大整数,如[3.15]=3,[0.7]=0,[-2.6]=-3)设函数,则函数的值域为( )
A.{-1,0} B.{0} C.{-1} D.{-1,0,1}
9.某市原来居民用电价为0.52元/kw?h,换装分时电表后,峰时段(早上八点到晚上九点)的电价0.55元/kw?h,谷时段(晚上九点到次日早上八点)的电价为0.35元/kw?h.对于一个平均每月用电量为200kw?h?的家庭,换装分时电表后,每月节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为( )【版权所有:21教育】
A.110kw?h B.114kw?h C.118kw?h D.120kw?h
10.国内快递1000g以内的包裹的邮资标准如下表:
运送距离x?(km)
0<x≤500
500<x≤1000
1000<x≤1500
1500<x≤2000
…
邮资y?(元)
5.00
6.00
7.00
8.00
…
如果某人在南京要快递800g的包裹到距南京1200km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元 C.7.00元 D.8.00元
11.从甲地到乙地途经丙地,其中甲、乙两地相距200千米,甲、丙两地相距离80千米,某人开汽车以40千米/小时的速度从甲地到达乙地,在丙地停留1小时,把汽车离开甲地的路程s表示为时间t(小时)的函数表达式是( )21cnjy.com
A.s=40t(0≤t≤5) B.s=40t(0≤t≤6) C. D.
二、填空题
12.函数f(x)=2x-log2(x+4)零点的个数为??? .
13.函数的值域是?? .
14.函数f(x)=?其中c>0,那么f(x)的零点是? ? .
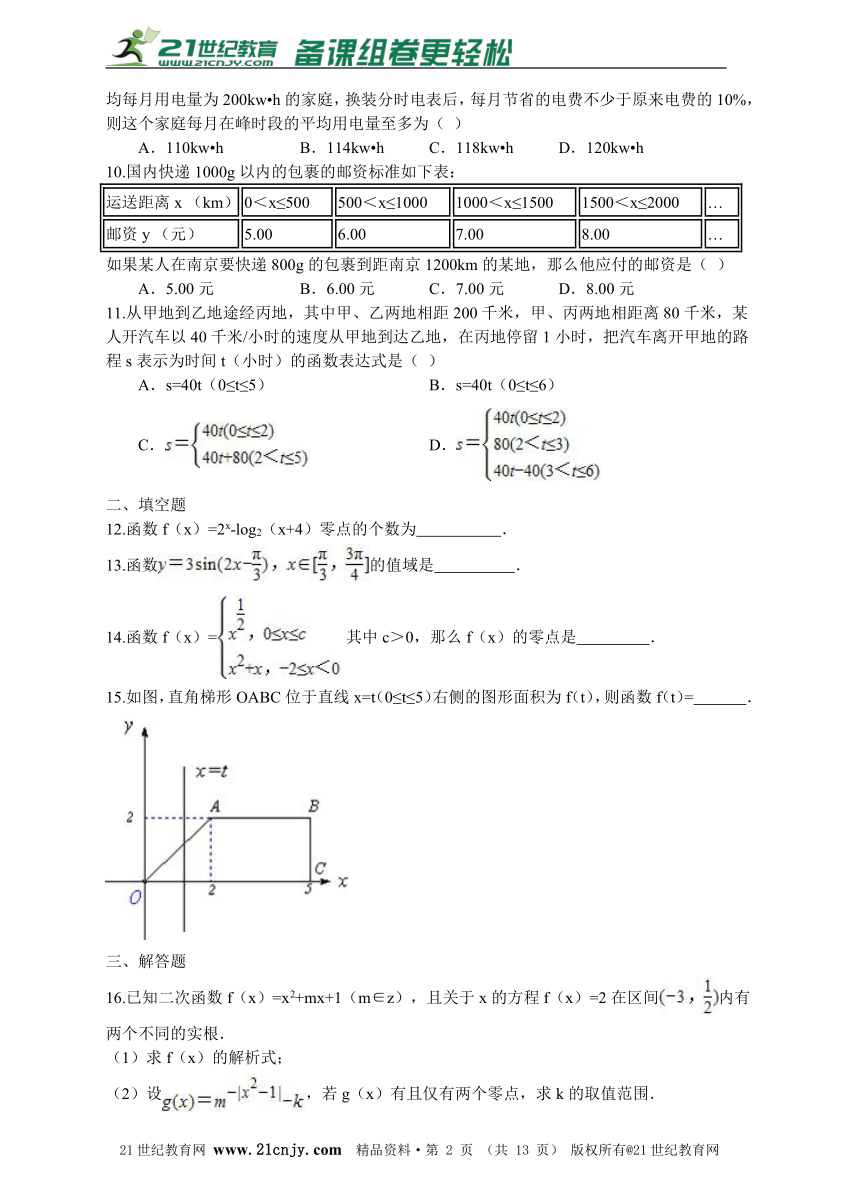
15.如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t),则函数f(t)=??? .
三、解答题
16.已知二次函数f(x)=x2+mx+1(m∈z),且关于x的方程f(x)=2在区间内有两个不同的实根. (1)求f(x)的解析式;21教育名师原创作品
(2)设,若g(x)有且仅有两个零点,求k的取值范围.
17.已知函数f(x)=, (1)在坐标系内画出函数f(x)大致图象; (2)分别求出f(a2+1)(a∈R),f(f(3))的值; (3)当-4≤x<3时,求f(x)取值的集合.
18.我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的. 某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定: ①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费a元; ②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付n元的超额费; ③每户每月的定额损耗费a不超过5元. (1)求每户每月水费y(元)与月用水量x(立方米)的函数关系; (2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
月份
用水量(立方米)
水费(元)
一
4
17
二
5
23
三
2.5
11
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.
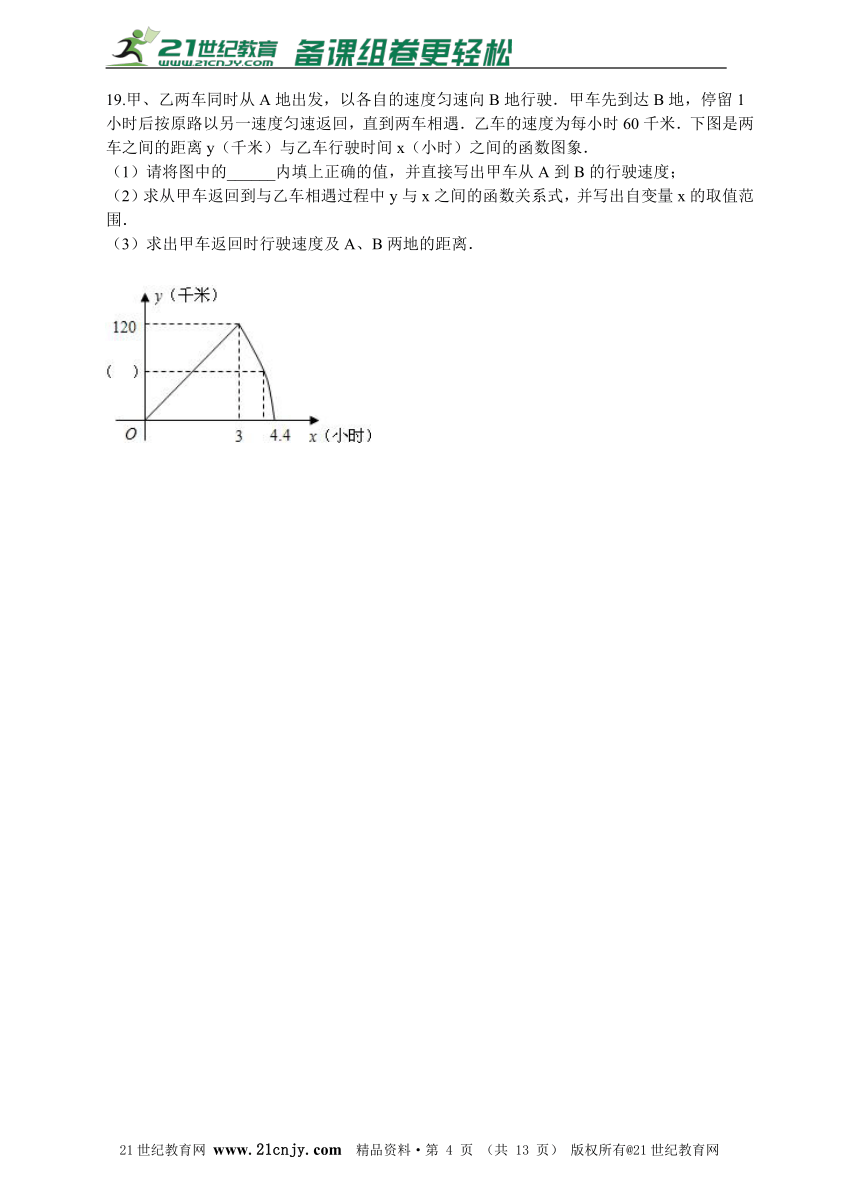
19.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象. (1)请将图中的______内填上正确的值,并直接写出甲车从A到B的行驶速度; (2)求从甲车返回到与乙车相遇过程中y与x之间的函数关系式,并写出自变量x的取值范围. (3)求出甲车返回时行驶速度及A、B两地的距离.21教育网
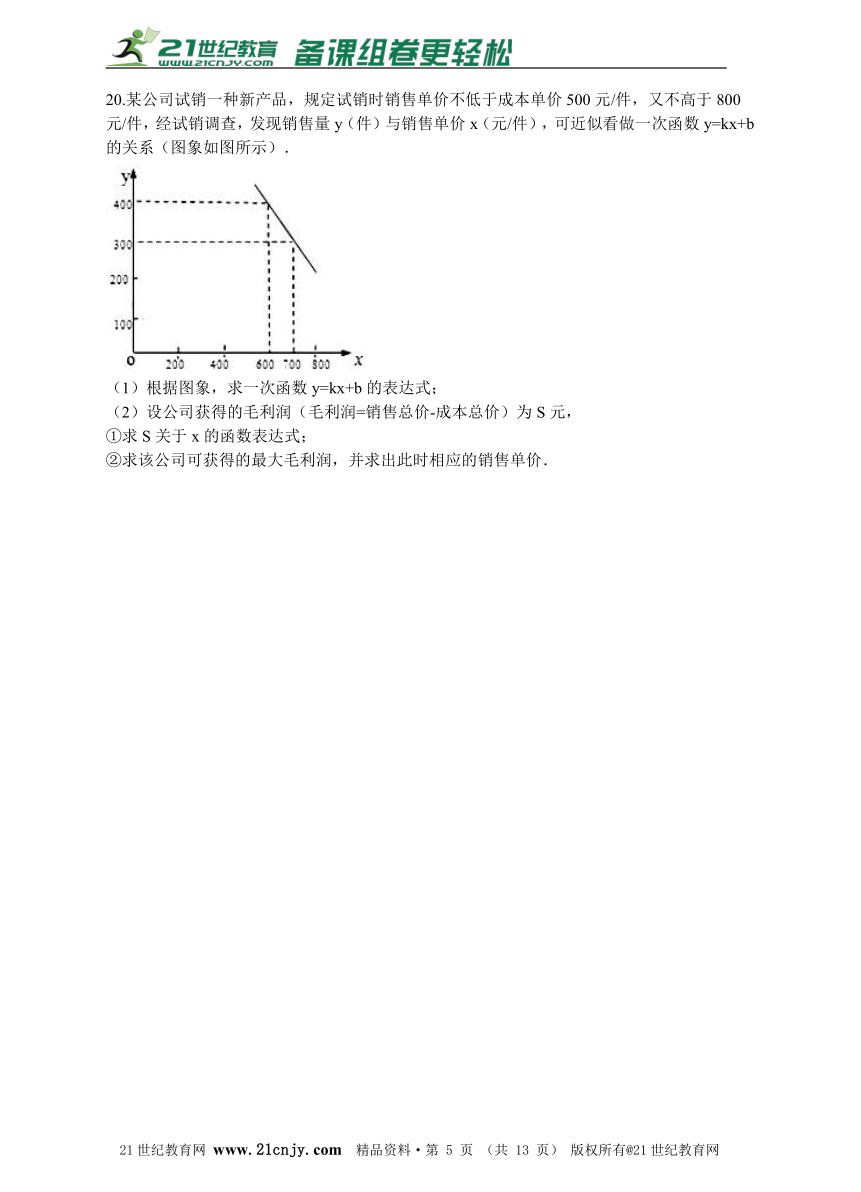
20.某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示).21世纪教育网版权所有
(1)根据图象,求一次函数y=kx+b的表达式; (2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元, ①求S关于x的函数表达式; ②求该公司可获得的最大毛利润,并求出此时相应的销售单价.21·cn·jy·com
参考答案及解析
1.D 【解析】由题意,不妨设a<b,则 ∵f(a)=f(b),∴-log3a=log3b,∴log3ab=0 ∴ab=1 2.Cwww.21-cn-jy.com
3.C 【解析】将64枚纪念币均分为两组,分别称量其重量, 假的一定在轻的哪一组,再将这一组(共32枚)均分为两组,称其重量, 这样一直均分下去,可以知道6次就能找出那枚假的,即最多只需称量6次. 4.C 【解析】由题意,f(x)唯一的零点在区间(1,3)、(1,4)、(1,5)内,可知该函数的唯一零点在区间(1,3)内,在其他区间不会存在零点.故A、B选项正确, 函数的零点可能在区间(2,3)内,也可能在(1,2)内,故C项不一定正确, 函数的零点可能在区间(2,3)内,也可能在(1,2)内,故函数在(2,4)内不一定有零点,D项正确. 5.C 【解析】根据循环结构的定义以及方程的根的精度的定义,循环结构的终止条件是两个根的差的绝对值小于精度, 即|x1-x2|<e, 6.B【来源:21·世纪·教育·网】
【解析】根据定义的运算法则化简函数f(x)=(x2-2)?(x-x2)的解析式,并求出f(x)的取值范围,函数y=f(x)-c的图象与x轴恰有两个公共点转化为y=f(x),y=c图象的交点问题,结合图象求得实数c的取值范围. 21·世纪*教育网
∴函数y=f(x)的图象与平行于y轴的直线最多只能有一个交点.(A)就不对了. B:由于两个函数的定义域不同,故不是同一个函数,错; C:根据零点存在性定理知,要求函数f(x)在区间[a,b]上连续才行,故其不正确; 8.A 【解析】由题意,g(x)=f(x)-==1--=-;f(-x)=-=; ∴g(-x)=-g(x),即g(x)是奇函数. 又∵2x>0,∴1+2x>1,∴,∴; 即 <g(-x)<.所以,g(x)<. 当x=0时,g(x)=g(-x)=0,y=[g(x)]+[g(-x)]=0; 当x≠0时,若x>0,则0<g(x)<,-<g(-x)<0, ∴y=[g(x)]+[g(-x)]=0+(-1)=-1, 若x<0,则y=[g(x)]+[g(-x)]=(-1)+0=-1. 所以函数y的值域为{0,-1}.
在丙地停留1小时,即2<t≤3,s=80; 当3<t≤6时,s=40(t-1); ∴汽车离开甲地的路程s表示为时间t(小时)的函数表达式是 12.2www-2-1-cnjy-com
【解析】由f(x)=2x-log2(x+4)=0,将函数转化为2x=log2(x+4),然后作出两个函数y=2x y=log2(x+4)在同一个坐标系中的图象,利用两个图象的交点个数判断函数零点个数. 21*cnjy*com
由f(x)=2x-log2(x+4)得2x=log2(x+4),设y=2x ,y=log2(x+4), 在同一个坐标系中作出两个函数y=2x ,y=log2(x+4)的图象如图: 由图象可知两个函数的交点为2个,
根据正弦函数图象则, 14.-1和0 【解析】函数f(x)=, 若0≤x≤c,f(x)=≥0,当x=0时,f(x)=0,x=0是f(x)的一个零点, 若-2≤x<0,f(x)=x2+x=x(x+1),令f(x)=0,可得x=0或x=-1,因为-2≤x<0,可得x=-1, 综上f(x)的零点是-1和0, 15. 【解析】由题意可知:当0<t≤2时,f(t)=2+2×3-t2=8-t2, 当2<t≤5 时,f(t)=2(5-t)=10-2t; 所以. 16.(1)f(x)=x2+2x+1 (2) 【解析】(1)由f(x)=2得,x2+mx-1=0, 则方程x2+mx-1=0在区间内有两个不同的实根, 即函数g(x)=x2+mx-1在区间内有两个不同的零点(图象与x轴有两个不同的交点), 由图得,log2k<-1或log2k=0, 解得, 故k的取值范围:. 17.(1)见解析 (2)11 (3)(-5,9] 【解析】【出处:21教育名师】
(1)∵函数f(x)=,其图象如图所示. (2)∵a2+1≥1, ∴f(a2+1)=4-(a2+1)2=3-2a2-a4,(a∈R), 因f(3)=-5, (2)解:∵0<a≤5, ∴9<9+a≤14. 由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于 最低限量m立方米. 将和分别代入(**), 得 两式相减,得n=6. 代入17=9+n(4-m)+a,得a=6m-16. 又三月份用水量为2.5立方米, 若m<2.5,将代入(**),得a=6m-13, 这与a=6m-16矛盾.(10分) ∴m≥2.5,即该家庭三月份用水量2.5立方米没有超最低限量. 将代入(*),得11=9+a, 由解得 故该家庭今年一、二月份用水超过最低限量,三月份用水没有超过最低限量,且m=3,n=6,
解得 甲车返回到与乙车相遇过程中y=-150x+660,x∈[4,4.4]; (3)甲车返回时行驶速度为150-60=90千米/小时;A、B两地相距100×3=300千米. 20.(1)y=-x+1000(500≤x≤800) (2)s=-x2+1500x-500000,(500≤x≤800)
该公司可获得的最大毛利润为62500元,此时相应的销售单价为750元/件. 【解析】(1)由图象可知,, 解得,, 所以y=-x+1000(500≤x≤800). (2)①由(1) S=x×y-500y =(-x+1000)(x-500) =-x2+1500x-500000,(500≤x≤800). ②由①可知,S=-(x-750)2+62500, 其图象开口向下,对称轴为x=750, 所以当x=750时,Smax=62500. 即该公司可获得的最大毛利润为62500元, 此时相应的销售单价为750元/件.
一、选择题
1.已知函数f(x)=|log3x|,若a≠b时,有f(a)=f(b),则( )
A.a<b<1 B.a>b>1 C.ab=3 D.ab=1
2.若f(x)=|x2-2x-3|,则方程f3(x)-4f2(x)-f(x)+4=0的根的个数为( )
A.5 B.6 C.7 D.9
3.因工作人员不慎将63枚真纪念币和一枚假纪念币混在了一起,从其外形无法分辨,仅仅知道假纪念币的重量要比真纪念币稍稍轻一点点,现用一台天平,通过比较重量的方法来找出那枚假纪念币,则最多只需称量( )次.2-1-c-n-j-y
A.4 B.5 C.6 D.7
4.已知f(x)唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下面命题错误的( )
A.函数f(x)在(1,2)或[2,3)内有零点 B.函数f(x)在(3,5)内无零点 C.函数f(x)在(2,5)内有零点 D.函数f(x)在(2,4)内不一定有零点21*cnjy*com
5.用二分法求方程的近似根,精确度为e,则循环结构的终止条件是( )
A.|x1-x2|>e B.x1=x2=e C.|x1-x2|<e D.x1<e<x22·1·c·n·j·y
6.对实数a与b,定义新运算“?”:设函数f(x)=(x2-2)?(x-x2),x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A. B. C. D.
7.下列说法正确的是( )
A.函数y=f(x)的图象与直线x=a可能有两个交点
B.函数y=log2x2与函数y=2log2x是同一函数
C.对于[a,b]上的函数y=f(x),若有f(a)?f(b)<0,那么函数y=f(x)在(a,b)内有零点【来源:21cnj*y.co*m】
D.对于指数函数y=ax(a>1)与幂函数y=xn(n>0),总存在一个x,当x>x时,就会有ax>xn
8.在计算机的算法语言中有一种函数[x]叫做高斯函数,它表示数x的整数部分(即小于等于x的最大整数,如[3.15]=3,[0.7]=0,[-2.6]=-3)设函数,则函数的值域为( )
A.{-1,0} B.{0} C.{-1} D.{-1,0,1}
9.某市原来居民用电价为0.52元/kw?h,换装分时电表后,峰时段(早上八点到晚上九点)的电价0.55元/kw?h,谷时段(晚上九点到次日早上八点)的电价为0.35元/kw?h.对于一个平均每月用电量为200kw?h?的家庭,换装分时电表后,每月节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为( )【版权所有:21教育】
A.110kw?h B.114kw?h C.118kw?h D.120kw?h
10.国内快递1000g以内的包裹的邮资标准如下表:
运送距离x?(km)
0<x≤500
500<x≤1000
1000<x≤1500
1500<x≤2000
…
邮资y?(元)
5.00
6.00
7.00
8.00
…
如果某人在南京要快递800g的包裹到距南京1200km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元 C.7.00元 D.8.00元
11.从甲地到乙地途经丙地,其中甲、乙两地相距200千米,甲、丙两地相距离80千米,某人开汽车以40千米/小时的速度从甲地到达乙地,在丙地停留1小时,把汽车离开甲地的路程s表示为时间t(小时)的函数表达式是( )21cnjy.com
A.s=40t(0≤t≤5) B.s=40t(0≤t≤6) C. D.
二、填空题
12.函数f(x)=2x-log2(x+4)零点的个数为??? .
13.函数的值域是?? .
14.函数f(x)=?其中c>0,那么f(x)的零点是? ? .
15.如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t),则函数f(t)=??? .
三、解答题
16.已知二次函数f(x)=x2+mx+1(m∈z),且关于x的方程f(x)=2在区间内有两个不同的实根. (1)求f(x)的解析式;21教育名师原创作品
(2)设,若g(x)有且仅有两个零点,求k的取值范围.
17.已知函数f(x)=, (1)在坐标系内画出函数f(x)大致图象; (2)分别求出f(a2+1)(a∈R),f(f(3))的值; (3)当-4≤x<3时,求f(x)取值的集合.
18.我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的. 某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定: ①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费a元; ②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付n元的超额费; ③每户每月的定额损耗费a不超过5元. (1)求每户每月水费y(元)与月用水量x(立方米)的函数关系; (2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
月份
用水量(立方米)
水费(元)
一
4
17
二
5
23
三
2.5
11
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.
19.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象. (1)请将图中的______内填上正确的值,并直接写出甲车从A到B的行驶速度; (2)求从甲车返回到与乙车相遇过程中y与x之间的函数关系式,并写出自变量x的取值范围. (3)求出甲车返回时行驶速度及A、B两地的距离.21教育网
20.某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件),可近似看做一次函数y=kx+b的关系(图象如图所示).21世纪教育网版权所有
(1)根据图象,求一次函数y=kx+b的表达式; (2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元, ①求S关于x的函数表达式; ②求该公司可获得的最大毛利润,并求出此时相应的销售单价.21·cn·jy·com
参考答案及解析
1.D 【解析】由题意,不妨设a<b,则 ∵f(a)=f(b),∴-log3a=log3b,∴log3ab=0 ∴ab=1 2.Cwww.21-cn-jy.com
3.C 【解析】将64枚纪念币均分为两组,分别称量其重量, 假的一定在轻的哪一组,再将这一组(共32枚)均分为两组,称其重量, 这样一直均分下去,可以知道6次就能找出那枚假的,即最多只需称量6次. 4.C 【解析】由题意,f(x)唯一的零点在区间(1,3)、(1,4)、(1,5)内,可知该函数的唯一零点在区间(1,3)内,在其他区间不会存在零点.故A、B选项正确, 函数的零点可能在区间(2,3)内,也可能在(1,2)内,故C项不一定正确, 函数的零点可能在区间(2,3)内,也可能在(1,2)内,故函数在(2,4)内不一定有零点,D项正确. 5.C 【解析】根据循环结构的定义以及方程的根的精度的定义,循环结构的终止条件是两个根的差的绝对值小于精度, 即|x1-x2|<e, 6.B【来源:21·世纪·教育·网】
【解析】根据定义的运算法则化简函数f(x)=(x2-2)?(x-x2)的解析式,并求出f(x)的取值范围,函数y=f(x)-c的图象与x轴恰有两个公共点转化为y=f(x),y=c图象的交点问题,结合图象求得实数c的取值范围. 21·世纪*教育网
∴函数y=f(x)的图象与平行于y轴的直线最多只能有一个交点.(A)就不对了. B:由于两个函数的定义域不同,故不是同一个函数,错; C:根据零点存在性定理知,要求函数f(x)在区间[a,b]上连续才行,故其不正确; 8.A 【解析】由题意,g(x)=f(x)-==1--=-;f(-x)=-=; ∴g(-x)=-g(x),即g(x)是奇函数. 又∵2x>0,∴1+2x>1,∴,∴; 即 <g(-x)<.所以,g(x)<. 当x=0时,g(x)=g(-x)=0,y=[g(x)]+[g(-x)]=0; 当x≠0时,若x>0,则0<g(x)<,-<g(-x)<0, ∴y=[g(x)]+[g(-x)]=0+(-1)=-1, 若x<0,则y=[g(x)]+[g(-x)]=(-1)+0=-1. 所以函数y的值域为{0,-1}.
在丙地停留1小时,即2<t≤3,s=80; 当3<t≤6时,s=40(t-1); ∴汽车离开甲地的路程s表示为时间t(小时)的函数表达式是 12.2www-2-1-cnjy-com
【解析】由f(x)=2x-log2(x+4)=0,将函数转化为2x=log2(x+4),然后作出两个函数y=2x y=log2(x+4)在同一个坐标系中的图象,利用两个图象的交点个数判断函数零点个数. 21*cnjy*com
由f(x)=2x-log2(x+4)得2x=log2(x+4),设y=2x ,y=log2(x+4), 在同一个坐标系中作出两个函数y=2x ,y=log2(x+4)的图象如图: 由图象可知两个函数的交点为2个,
根据正弦函数图象则, 14.-1和0 【解析】函数f(x)=, 若0≤x≤c,f(x)=≥0,当x=0时,f(x)=0,x=0是f(x)的一个零点, 若-2≤x<0,f(x)=x2+x=x(x+1),令f(x)=0,可得x=0或x=-1,因为-2≤x<0,可得x=-1, 综上f(x)的零点是-1和0, 15. 【解析】由题意可知:当0<t≤2时,f(t)=2+2×3-t2=8-t2, 当2<t≤5 时,f(t)=2(5-t)=10-2t; 所以. 16.(1)f(x)=x2+2x+1 (2) 【解析】(1)由f(x)=2得,x2+mx-1=0, 则方程x2+mx-1=0在区间内有两个不同的实根, 即函数g(x)=x2+mx-1在区间内有两个不同的零点(图象与x轴有两个不同的交点), 由图得,log2k<-1或log2k=0, 解得, 故k的取值范围:. 17.(1)见解析 (2)11 (3)(-5,9] 【解析】【出处:21教育名师】
(1)∵函数f(x)=,其图象如图所示. (2)∵a2+1≥1, ∴f(a2+1)=4-(a2+1)2=3-2a2-a4,(a∈R), 因f(3)=-5, (2)解:∵0<a≤5, ∴9<9+a≤14. 由于该家庭今年一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于 最低限量m立方米. 将和分别代入(**), 得 两式相减,得n=6. 代入17=9+n(4-m)+a,得a=6m-16. 又三月份用水量为2.5立方米, 若m<2.5,将代入(**),得a=6m-13, 这与a=6m-16矛盾.(10分) ∴m≥2.5,即该家庭三月份用水量2.5立方米没有超最低限量. 将代入(*),得11=9+a, 由解得 故该家庭今年一、二月份用水超过最低限量,三月份用水没有超过最低限量,且m=3,n=6,
解得 甲车返回到与乙车相遇过程中y=-150x+660,x∈[4,4.4]; (3)甲车返回时行驶速度为150-60=90千米/小时;A、B两地相距100×3=300千米. 20.(1)y=-x+1000(500≤x≤800) (2)s=-x2+1500x-500000,(500≤x≤800)
该公司可获得的最大毛利润为62500元,此时相应的销售单价为750元/件. 【解析】(1)由图象可知,, 解得,, 所以y=-x+1000(500≤x≤800). (2)①由(1) S=x×y-500y =(-x+1000)(x-500) =-x2+1500x-500000,(500≤x≤800). ②由①可知,S=-(x-750)2+62500, 其图象开口向下,对称轴为x=750, 所以当x=750时,Smax=62500. 即该公司可获得的最大毛利润为62500元, 此时相应的销售单价为750元/件.
