大庆市杜蒙县2016-2017学年八年级上期中数学试卷(解析版)
文档属性
| 名称 | 大庆市杜蒙县2016-2017学年八年级上期中数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-29 00:00:00 | ||
图片预览




文档简介
2016-2017学年黑龙江省大庆市杜蒙县八年级(上)期中数学试卷(五四学制)
一、认真选一选(本大题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知两个三角形相似,其中一个三角形的两个角分别为72°、63°,则另一个三角形的最小的内角为( )
A.72°
B.63°
C.45°
D.不能确定
2.若3x﹣2y=0,则+1等于( )
A.
B.
C.
D.﹣
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
4.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm
B.13.6cm
C.32.36cm
D.7.64cm
5.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根
D.使最简公分母的值为零的解是增根
6.无论x取何值,总是有意义的分式是( )
A.
B.
C.
D.
7.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个
B.可以有2个
C.有2个以上,但有限
D.有无数个
9.某厂接受为四川灾区生产活动板房的任务,计划在30天内完成,若每天多生产6套,则25天完成且还多生产10套,问原计划每天生产多少套板房?设原计划每天生产x套,列方程式是( )
A.
B.
C.
D.
10.若===k,则k的值为( )
A.2
B.﹣1
C.2或﹣1
D.﹣2或1
二、仔细填一填(本大题共10个小题;每空3分,共30分.)
11.分式当 时分式的值为零,当 时,分式有意义.
12.若方程﹣=8有增根,则增根是 .
13.若关于x的分式方程﹣2=无解,则m= .
14.东东和爸爸到广场散步,爸爸的身高是176cm,东东的身高是156cm,在同一时刻爸爸的影长是88cm,那么东东的影长是 cm.
15.已知==,则的值是 .
16.如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= .
17.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 米.
18.如图:AB、CD相交于O,且∠A=∠C,若OA=3,OD=4,OB=2,则OC= .
19.如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF= .
三.解答题:
20.计算下列各式:
(1)++
(2)3xy2÷
(3)﹣+
(4) .
21.如图,已知AD、BE是△ABC的两条高,试说明AD BC=BE AC.
22.解下列分式方程.
(1)=
(2)+=
(3)=﹣2
(4)=﹣.
23.先化简(﹣a+2)÷,再从﹣2,2,4,0中选择一个合适的数代入求值.
24.阅读下面对话:
小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
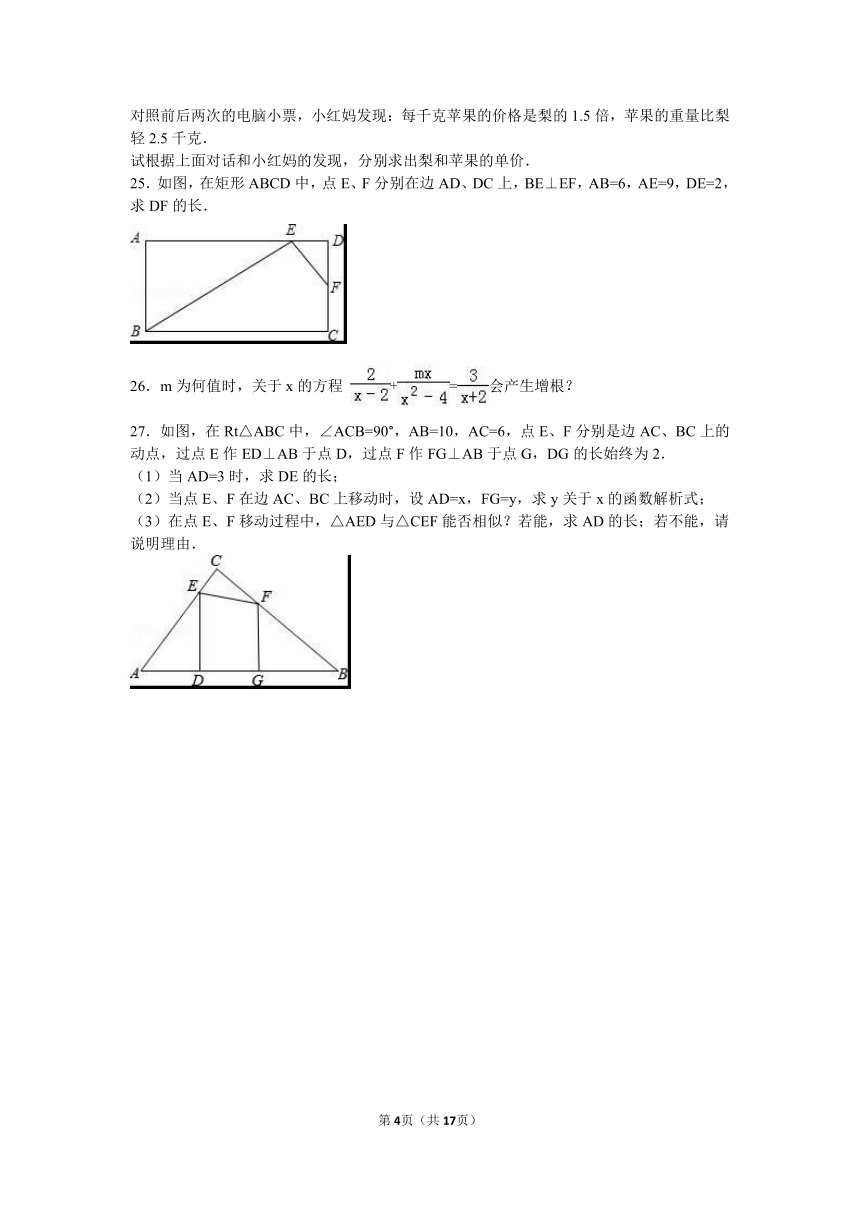
25.如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.
26.m为何值时,关于x的方程
+=会产生增根?
27.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设AD=x,FG=y,求y关于x的函数解析式;
(3)在点E、F移动过程中,△AED与△CEF能否相似?若能,求AD的长;若不能,请说明理由.
2016-2017学年黑龙江省大庆市杜蒙县八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、认真选一选(本大题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知两个三角形相似,其中一个三角形的两个角分别为72°、63°,则另一个三角形的最小的内角为( )
A.72°
B.63°
C.45°
D.不能确定
【考点】相似三角形的性质.
【分析】根据相似三角形的对应角相等,可知两个三角形的最小内角对应相等,可由三角形内角和定理求出其中一个三角形的最小内角,即可得出本题的结果.
【解答】解:由三角形内角和定理知:三角形的另外一角是180°﹣72°﹣63°=45°;
由于45°<63°<72°,所以45°角是此三角形的最小内角;
已知两个三角形相似,因此另一个三角形的最小内角也应该是45°;故选C.
2.若3x﹣2y=0,则+1等于( )
A.
B.
C.
D.﹣
【考点】比例的性质.
【分析】根据等式的性质,可得,根据有理数的加法,可得答案.
【解答】解:由题意,得
3x=2y.
两边都除以3y,得
=.
+1=+1=,
故选:C.
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
【考点】相似图形.
【分析】利用“对应角相等,对应边的比也相等的多边形是相似形”逐一进行判断即可.
【解答】解:A、任意两个等腰三角形都相似,错误;
B、任意两个菱形都相似,错误;
C、任意两个正五边形都相似,正确;
D、对应角相等的两个多边形相似,错误,
故选C.
4.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm
B.13.6cm
C.32.36cm
D.7.64cm
【考点】黄金分割.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
【解答】解:方法1:设书的宽为x,则有(20+x):20=20:x,解得x=12.36cm.
方法2:书的宽为20×0.618=12.36cm.
故选A.
5.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根
D.使最简公分母的值为零的解是增根
【考点】分式方程的增根.
【分析】分式方程的增根是最简公分母为零时,未知数的值.
【解答】解:分式方程的增根是使最简公分母的值为零的解.
故选D.
6.无论x取何值,总是有意义的分式是( )
A.
B.
C.
D.
【考点】分式有意义的条件.
【分析】根据分式有意义的条件对各选项进行判断.
【解答】解:A、当2x+1≠0时,分式有意义,即x≠﹣,所以A选项错误;
B、当x为任何实数,分式有意义,所以B选项正确;
C、当x3+1≠0时,分式有意义,即x≠﹣1,所以C选项错误;
D、当x2≠0时,分式有意义,即x≠0,所以D选项错误.
故选B.
7.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
【考点】相似三角形的判定.
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例,做题即可.
【解答】解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个
B.可以有2个
C.有2个以上,但有限
D.有无数个
【考点】勾股定理;相似三角形的判定与性质.
【分析】两条边长分别是6和8的直角三角形有两种可能,即已知边均为直角边或者8为斜边,运用勾股定理分别求出第三边后,和另外三角形构成相似三角形,利用对应边成比例即可解答.
【解答】解:根据题意,两条边长分别是6和8的直角三角形有两种可能,一种是6和8为直角边,那么根据勾股定理可知斜边为10;另一种可能是6是直角边,而8是斜边,那么根据勾股定理可知另一条直角边为.
所以另一个与它相似的直角三角形也有两种可能,
第一种是,解得x=5;
第二种是,解得x=.所以可以有2个.
故选:B.
9.某厂接受为四川灾区生产活动板房的任务,计划在30天内完成,若每天多生产6套,则25天完成且还多生产10套,问原计划每天生产多少套板房?设原计划每天生产x套,列方程式是( )
A.
B.
C.
D.
【考点】由实际问题抽象出分式方程.
【分析】设原计划每天生产x套,先求出实际25天完成的套数,再求出实际的工作效率=,最后依据工作时间=工作总量÷工作效率解答.
【解答】解:由分析可得列方程式是:
=25.
故选B.
10.若===k,则k的值为( )
A.2
B.﹣1
C.2或﹣1
D.﹣2或1
【考点】比例的性质.
【分析】分①a+b+c=0时,用c表示出a+b,然后求解,②a+b+c≠0时,利用等比性质列式计算即可得解.
【解答】解:①a+b+c=0时,a+b=﹣c,
所以,k===﹣1;
②a+b+c≠0时,
=====2,
所以,k=2,
综上所述,k的值为2或﹣1.
故选C.
二、仔细填一填(本大题共10个小题;每空3分,共30分.)
11.分式当 x=﹣3 时分式的值为零,当 x≠ 时,分式有意义.
【考点】分式的值为零的条件;分式有意义的条件.
【分析】要使分式的值为0,必须分式分子的值为0,并且分母的值不为0.分母的值是0时分式没有意义.
【解答】解:由分子x2﹣9=0解得:x=±3,
而x=3时,分母x﹣3=0
所以x=﹣3.
由1﹣2x≠0解得:x≠.
故第一个空填﹣3,第二个空填≠.
12.若方程﹣=8有增根,则增根是 x=7 .
【考点】分式方程的增根.
【分析】增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.
【解答】解:∵分式方程﹣=8有增根,
∴x﹣7=0
∴原方程增根为x=7,
故答案为x=7.
13.若关于x的分式方程﹣2=无解,则m= .
【考点】分式方程的解.
【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答】解:去分母,得x﹣2(x﹣3)=m2,
把x=3代入得3﹣2(3﹣3)=m2,
解得:m=±.
故答案是:.
14.东东和爸爸到广场散步,爸爸的身高是176cm,东东的身高是156cm,在同一时刻爸爸的影长是88cm,那么东东的影长是 78 cm.
【考点】相似三角形的应用.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【解答】解:据相同时刻的物高与影长成比例,
设东东的身高为xm,则可列比例为,
解得x=78cm,
故东东的影长78cm.
15.已知==,则的值是 7 .
【考点】比例的性质.
【分析】设===t,利用比例的性质可用t分别表示出x、y、z,然后把x、y、z分别代入原式,再进行分式的计算即可.
【解答】解:设===t,则x=2t,y=3t,z=0.5t,
所以原式==7.
故答案为7.
16.如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= 8 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】首先由平行四边形的性质可知BC∥AD,然后证明△BMP∽△DAP,再根据相似三角形的对应边成比例,得出AP:PM=AD:BM,从而求出AP的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴BC∥AD,AD=BC,
∴∠PBM=∠PDA,∠PMB=∠PAD,
∴△BMP∽△DAP,
∴AP:PM=AD:BM,
又∵M为BC边的中点,
∴BC=2BM,
∴AD=2BM,
∴AP=2PM=8.
17.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 8 米.
【考点】相似三角形的应用.
【分析】Rt△ABP和Rt△CDP相似,即1.2:1.8=CD:12求得该古城墙的高度.
【解答】解:由题意知:光线AP与光线PC,∠APB=∠CPD,
所以Rt△ABP∽Rt△CDP,
所以AB:BP=CD:PD
即1.2:1.8=CD:12,
解得CD=8米.
故答案为:8.
18.如图:AB、CD相交于O,且∠A=∠C,若OA=3,OD=4,OB=2,则OC= .
【考点】相似三角形的判定与性质.
【分析】首先根据已知条件证△AOD∽△COB,然后根据相似三角形的对应线段成比例求出OC的长.
【解答】解:∵∠A=∠C,∠AOD=∠BOC,
∴△AOD∽△COB;
∴,即OC=,
又∵OA=3,OD=4,OB=2,
∴OC=
19.如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF= 14.4 .
【考点】平行线分线段成比例;梯形.
【分析】过点A作AG∥CD,交BC于点G,交EF于点H,则可知AD=HF=CG=12,BG=6,又由AE:EB=2:3可求得AE:AB=2:5,利用平行线分线段成比例可求得EH,则可得出答案.
【解答】解:过点A作AG∥CD,交BC于点G,交EF于点H,
∵AD∥BC,EF∥BC,
∴AD=FH=GC=12cm,BG=BC﹣CG=18﹣12=6,
∵=,
∴=,
∴==,
即=,
解得EH=,
∴EF=EH+HF=+12=,
故答案为:14.4.
三.解答题:
20.计算下列各式:
(1)++
(2)3xy2÷
(3)﹣+
(4) .
【考点】分式的混合运算.
【分析】根据分式的基本性质即可求出答案.
【解答】解:(1)原式=++=;
(2)原式=3xy2×=;
(3)原式=﹣﹣===﹣;
(4)原式= =
21.如图,已知AD、BE是△ABC的两条高,试说明AD BC=BE AC.
【考点】相似三角形的判定与性质.
【分析】根据三角形高的定义可得到相等的直角,再由公共角,可证得△ADC∽△BEC,再根据相似三角形的性质:对应边成比例变形即可求得.
【解答】证明:∵AD、BE是△ABC的高,
∴∠ADC=∠BEC.
∵∠C=∠C,
∴△ADC∽△BEC.
∴AD:BE=AC:BC.
∴AD BC=BE AC.
22.解下列分式方程.
(1)=
(2)+=
(3)=﹣2
(4)=﹣.
【考点】解分式方程.
【分析】各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:3x=x﹣2,
解得:x=﹣1,
检验x=﹣1是分式方程的解;
(2)去分母得:x﹣1+2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:1﹣x=﹣1﹣2x+4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(4)去分母得:1=3x﹣1+4,
解得:x=﹣,
经检验x=﹣是分式方程的解.
23.先化简(﹣a+2)÷,再从﹣2,2,4,0中选择一个合适的数代入求值.
【考点】分式的化简求值.
【分析】根据分式的混合运算顺序和运算法则化简原式,再将符合分式有意义的a的值,即4代入计算可得.
【解答】解:原式=(﹣)
=
=,
当a=4时,原式==.
24.阅读下面对话:
小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
【考点】一元一次方程的应用.
【分析】设每千克梨的价格是x元,则每千克苹果的价格是1.5x元.根据苹果的重量比梨轻2.5千克这个等量关系列方程求解.
【解答】解:设每千克梨的价格是x元,则每千克苹果的价格是1.5x元.
则有:,
解得:x=4,
经检验得x=4是原方程的根且符合题意,
1.5x=6.
答:梨和苹果的单价分别为4元/千克和6元/千克.
25.如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.
【考点】矩形的性质.
【分析】由在矩形ABCD中,BE⊥EF,易证得△ABE∽△DEF,然后由相似三角形的对应边成比例,求得答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠ABE+∠AEB=90°,
∵BE⊥EF,
∴∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF,
∴=,
∴=,
解得:DF=3.
26.m为何值时,关于x的方程
+=会产生增根?
【考点】分式方程的增根.
【分析】先去分母得2(x+2)+mx=3(x﹣2),整理得(m﹣1)x+10=0,由于关于x的方程
+=会产生增根,则(x+2)(x﹣2)=0,解得x=﹣2
或x=2,然后把x=﹣2
和x=2分别代入(m﹣1)x+10=0即可得到m的值.
【解答】解:原方程化为+=,
方程两边同时乘以(x+2)(x﹣2)
得2(x+2)+mx=3(x﹣2),
整理得(m﹣1)x+10=0,
∵关于x的方程
+=会产生增根,
∴(x+2)(x﹣2)=0,
∴x=﹣2
或x=2,
∴当x=﹣2时,(m﹣1)×(﹣2)+10=0,解得m=6,
当x=2时,(m﹣1)×2+10=0,解得m=﹣4,
∴m=﹣4或m=6时,原方程会产生增根.
27.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设AD=x,FG=y,求y关于x的函数解析式;
(3)在点E、F移动过程中,△AED与△CEF能否相似?若能,求AD的长;若不能,请说明理由.
【考点】相似形综合题.
【分析】(1)由△ADE∽△ACB,得=,由此即可解决问题.
(2)由△BGF∽△BCA,得=,由此即可解决问题.
(3)分两种情形①当∠A=∠CEF时,△ADE∽△ECF,
=.②当∠A=∠CFE时,△ADE∽△FCE,
=,分别列出方程即可解决问题.
【解答】解:(1)∵∠ACB=90°,AB=10,AC=6
∴BC=8∵ED⊥AB,
∴∠ADE=∠ACB=90°
又∵∠A=∠A,
∴△ADE∽△ACB,
∴=,
∴=,
∴DE=4.
(2)∵FG⊥AB,
∴∠BGF=∠BCA=90°,
又∵∠B=∠B,
∴△BGF∽△BCA,
∴=,
∴=,
∴y=﹣x+6.
(3)由(1)(2)可得:AE=x,BF=10﹣x,
∴CE=6﹣x,CF=x﹣2,
当∠A=∠CEF时,△ADE∽△ECF,
∴=.
∴=,
解得:x=;
当∠A=∠CFE时,△ADE∽△FCE,
∴=,
∴=,
解得:,
∴当AD的长为或时△AED与△CEF相似.
2016年11月29日
第1页(共17页)
一、认真选一选(本大题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知两个三角形相似,其中一个三角形的两个角分别为72°、63°,则另一个三角形的最小的内角为( )
A.72°
B.63°
C.45°
D.不能确定
2.若3x﹣2y=0,则+1等于( )
A.
B.
C.
D.﹣
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
4.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm
B.13.6cm
C.32.36cm
D.7.64cm
5.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根
D.使最简公分母的值为零的解是增根
6.无论x取何值,总是有意义的分式是( )
A.
B.
C.
D.
7.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个
B.可以有2个
C.有2个以上,但有限
D.有无数个
9.某厂接受为四川灾区生产活动板房的任务,计划在30天内完成,若每天多生产6套,则25天完成且还多生产10套,问原计划每天生产多少套板房?设原计划每天生产x套,列方程式是( )
A.
B.
C.
D.
10.若===k,则k的值为( )
A.2
B.﹣1
C.2或﹣1
D.﹣2或1
二、仔细填一填(本大题共10个小题;每空3分,共30分.)
11.分式当 时分式的值为零,当 时,分式有意义.
12.若方程﹣=8有增根,则增根是 .
13.若关于x的分式方程﹣2=无解,则m= .
14.东东和爸爸到广场散步,爸爸的身高是176cm,东东的身高是156cm,在同一时刻爸爸的影长是88cm,那么东东的影长是 cm.
15.已知==,则的值是 .
16.如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= .
17.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 米.
18.如图:AB、CD相交于O,且∠A=∠C,若OA=3,OD=4,OB=2,则OC= .
19.如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF= .
三.解答题:
20.计算下列各式:
(1)++
(2)3xy2÷
(3)﹣+
(4) .
21.如图,已知AD、BE是△ABC的两条高,试说明AD BC=BE AC.
22.解下列分式方程.
(1)=
(2)+=
(3)=﹣2
(4)=﹣.
23.先化简(﹣a+2)÷,再从﹣2,2,4,0中选择一个合适的数代入求值.
24.阅读下面对话:
小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
25.如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.
26.m为何值时,关于x的方程
+=会产生增根?
27.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设AD=x,FG=y,求y关于x的函数解析式;
(3)在点E、F移动过程中,△AED与△CEF能否相似?若能,求AD的长;若不能,请说明理由.
2016-2017学年黑龙江省大庆市杜蒙县八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、认真选一选(本大题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知两个三角形相似,其中一个三角形的两个角分别为72°、63°,则另一个三角形的最小的内角为( )
A.72°
B.63°
C.45°
D.不能确定
【考点】相似三角形的性质.
【分析】根据相似三角形的对应角相等,可知两个三角形的最小内角对应相等,可由三角形内角和定理求出其中一个三角形的最小内角,即可得出本题的结果.
【解答】解:由三角形内角和定理知:三角形的另外一角是180°﹣72°﹣63°=45°;
由于45°<63°<72°,所以45°角是此三角形的最小内角;
已知两个三角形相似,因此另一个三角形的最小内角也应该是45°;故选C.
2.若3x﹣2y=0,则+1等于( )
A.
B.
C.
D.﹣
【考点】比例的性质.
【分析】根据等式的性质,可得,根据有理数的加法,可得答案.
【解答】解:由题意,得
3x=2y.
两边都除以3y,得
=.
+1=+1=,
故选:C.
3.下列说法正确的是( )
A.任意两个等腰三角形都相似
B.任意两个菱形都相似
C.任意两个正五边形都相似
D.对应角相等的两个多边形相似
【考点】相似图形.
【分析】利用“对应角相等,对应边的比也相等的多边形是相似形”逐一进行判断即可.
【解答】解:A、任意两个等腰三角形都相似,错误;
B、任意两个菱形都相似,错误;
C、任意两个正五边形都相似,正确;
D、对应角相等的两个多边形相似,错误,
故选C.
4.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为( )
A.12.36cm
B.13.6cm
C.32.36cm
D.7.64cm
【考点】黄金分割.
【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值()叫做黄金比.
【解答】解:方法1:设书的宽为x,则有(20+x):20=20:x,解得x=12.36cm.
方法2:书的宽为20×0.618=12.36cm.
故选A.
5.下列关于分式方程增根的说法正确的是( )
A.使所有的分母的值都为零的解是增根
B.分式方程的解为零就是增根
C.使分子的值为零的解就是增根
D.使最简公分母的值为零的解是增根
【考点】分式方程的增根.
【分析】分式方程的增根是最简公分母为零时,未知数的值.
【解答】解:分式方程的增根是使最简公分母的值为零的解.
故选D.
6.无论x取何值,总是有意义的分式是( )
A.
B.
C.
D.
【考点】分式有意义的条件.
【分析】根据分式有意义的条件对各选项进行判断.
【解答】解:A、当2x+1≠0时,分式有意义,即x≠﹣,所以A选项错误;
B、当x为任何实数,分式有意义,所以B选项正确;
C、当x3+1≠0时,分式有意义,即x≠﹣1,所以C选项错误;
D、当x2≠0时,分式有意义,即x≠0,所以D选项错误.
故选B.
7.下列四个三角形中,与图中的三角形相似的是( )
A.
B.
C.
D.
【考点】相似三角形的判定.
【分析】本题主要应用两三角形相似的判定定理,三边对应成比例,做题即可.
【解答】解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个
B.可以有2个
C.有2个以上,但有限
D.有无数个
【考点】勾股定理;相似三角形的判定与性质.
【分析】两条边长分别是6和8的直角三角形有两种可能,即已知边均为直角边或者8为斜边,运用勾股定理分别求出第三边后,和另外三角形构成相似三角形,利用对应边成比例即可解答.
【解答】解:根据题意,两条边长分别是6和8的直角三角形有两种可能,一种是6和8为直角边,那么根据勾股定理可知斜边为10;另一种可能是6是直角边,而8是斜边,那么根据勾股定理可知另一条直角边为.
所以另一个与它相似的直角三角形也有两种可能,
第一种是,解得x=5;
第二种是,解得x=.所以可以有2个.
故选:B.
9.某厂接受为四川灾区生产活动板房的任务,计划在30天内完成,若每天多生产6套,则25天完成且还多生产10套,问原计划每天生产多少套板房?设原计划每天生产x套,列方程式是( )
A.
B.
C.
D.
【考点】由实际问题抽象出分式方程.
【分析】设原计划每天生产x套,先求出实际25天完成的套数,再求出实际的工作效率=,最后依据工作时间=工作总量÷工作效率解答.
【解答】解:由分析可得列方程式是:
=25.
故选B.
10.若===k,则k的值为( )
A.2
B.﹣1
C.2或﹣1
D.﹣2或1
【考点】比例的性质.
【分析】分①a+b+c=0时,用c表示出a+b,然后求解,②a+b+c≠0时,利用等比性质列式计算即可得解.
【解答】解:①a+b+c=0时,a+b=﹣c,
所以,k===﹣1;
②a+b+c≠0时,
=====2,
所以,k=2,
综上所述,k的值为2或﹣1.
故选C.
二、仔细填一填(本大题共10个小题;每空3分,共30分.)
11.分式当 x=﹣3 时分式的值为零,当 x≠ 时,分式有意义.
【考点】分式的值为零的条件;分式有意义的条件.
【分析】要使分式的值为0,必须分式分子的值为0,并且分母的值不为0.分母的值是0时分式没有意义.
【解答】解:由分子x2﹣9=0解得:x=±3,
而x=3时,分母x﹣3=0
所以x=﹣3.
由1﹣2x≠0解得:x≠.
故第一个空填﹣3,第二个空填≠.
12.若方程﹣=8有增根,则增根是 x=7 .
【考点】分式方程的增根.
【分析】增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.
【解答】解:∵分式方程﹣=8有增根,
∴x﹣7=0
∴原方程增根为x=7,
故答案为x=7.
13.若关于x的分式方程﹣2=无解,则m= .
【考点】分式方程的解.
【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答】解:去分母,得x﹣2(x﹣3)=m2,
把x=3代入得3﹣2(3﹣3)=m2,
解得:m=±.
故答案是:.
14.东东和爸爸到广场散步,爸爸的身高是176cm,东东的身高是156cm,在同一时刻爸爸的影长是88cm,那么东东的影长是 78 cm.
【考点】相似三角形的应用.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
【解答】解:据相同时刻的物高与影长成比例,
设东东的身高为xm,则可列比例为,
解得x=78cm,
故东东的影长78cm.
15.已知==,则的值是 7 .
【考点】比例的性质.
【分析】设===t,利用比例的性质可用t分别表示出x、y、z,然后把x、y、z分别代入原式,再进行分式的计算即可.
【解答】解:设===t,则x=2t,y=3t,z=0.5t,
所以原式==7.
故答案为7.
16.如图:M为平行四边形ABCD的BC边的中点,AM交BD于点P,若PM=4,则AP= 8 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】首先由平行四边形的性质可知BC∥AD,然后证明△BMP∽△DAP,再根据相似三角形的对应边成比例,得出AP:PM=AD:BM,从而求出AP的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴BC∥AD,AD=BC,
∴∠PBM=∠PDA,∠PMB=∠PAD,
∴△BMP∽△DAP,
∴AP:PM=AD:BM,
又∵M为BC边的中点,
∴BC=2BM,
∴AD=2BM,
∴AP=2PM=8.
17.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 8 米.
【考点】相似三角形的应用.
【分析】Rt△ABP和Rt△CDP相似,即1.2:1.8=CD:12求得该古城墙的高度.
【解答】解:由题意知:光线AP与光线PC,∠APB=∠CPD,
所以Rt△ABP∽Rt△CDP,
所以AB:BP=CD:PD
即1.2:1.8=CD:12,
解得CD=8米.
故答案为:8.
18.如图:AB、CD相交于O,且∠A=∠C,若OA=3,OD=4,OB=2,则OC= .
【考点】相似三角形的判定与性质.
【分析】首先根据已知条件证△AOD∽△COB,然后根据相似三角形的对应线段成比例求出OC的长.
【解答】解:∵∠A=∠C,∠AOD=∠BOC,
∴△AOD∽△COB;
∴,即OC=,
又∵OA=3,OD=4,OB=2,
∴OC=
19.如图,梯形ABCD中,AD∥BC∥EF,AE:EB=2:3,AD=12,则BC=18,则EF= 14.4 .
【考点】平行线分线段成比例;梯形.
【分析】过点A作AG∥CD,交BC于点G,交EF于点H,则可知AD=HF=CG=12,BG=6,又由AE:EB=2:3可求得AE:AB=2:5,利用平行线分线段成比例可求得EH,则可得出答案.
【解答】解:过点A作AG∥CD,交BC于点G,交EF于点H,
∵AD∥BC,EF∥BC,
∴AD=FH=GC=12cm,BG=BC﹣CG=18﹣12=6,
∵=,
∴=,
∴==,
即=,
解得EH=,
∴EF=EH+HF=+12=,
故答案为:14.4.
三.解答题:
20.计算下列各式:
(1)++
(2)3xy2÷
(3)﹣+
(4) .
【考点】分式的混合运算.
【分析】根据分式的基本性质即可求出答案.
【解答】解:(1)原式=++=;
(2)原式=3xy2×=;
(3)原式=﹣﹣===﹣;
(4)原式= =
21.如图,已知AD、BE是△ABC的两条高,试说明AD BC=BE AC.
【考点】相似三角形的判定与性质.
【分析】根据三角形高的定义可得到相等的直角,再由公共角,可证得△ADC∽△BEC,再根据相似三角形的性质:对应边成比例变形即可求得.
【解答】证明:∵AD、BE是△ABC的高,
∴∠ADC=∠BEC.
∵∠C=∠C,
∴△ADC∽△BEC.
∴AD:BE=AC:BC.
∴AD BC=BE AC.
22.解下列分式方程.
(1)=
(2)+=
(3)=﹣2
(4)=﹣.
【考点】解分式方程.
【分析】各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:3x=x﹣2,
解得:x=﹣1,
检验x=﹣1是分式方程的解;
(2)去分母得:x﹣1+2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:1﹣x=﹣1﹣2x+4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(4)去分母得:1=3x﹣1+4,
解得:x=﹣,
经检验x=﹣是分式方程的解.
23.先化简(﹣a+2)÷,再从﹣2,2,4,0中选择一个合适的数代入求值.
【考点】分式的化简求值.
【分析】根据分式的混合运算顺序和运算法则化简原式,再将符合分式有意义的a的值,即4代入计算可得.
【解答】解:原式=(﹣)
=
=,
当a=4时,原式==.
24.阅读下面对话:
小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
【考点】一元一次方程的应用.
【分析】设每千克梨的价格是x元,则每千克苹果的价格是1.5x元.根据苹果的重量比梨轻2.5千克这个等量关系列方程求解.
【解答】解:设每千克梨的价格是x元,则每千克苹果的价格是1.5x元.
则有:,
解得:x=4,
经检验得x=4是原方程的根且符合题意,
1.5x=6.
答:梨和苹果的单价分别为4元/千克和6元/千克.
25.如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求DF的长.
【考点】矩形的性质.
【分析】由在矩形ABCD中,BE⊥EF,易证得△ABE∽△DEF,然后由相似三角形的对应边成比例,求得答案.
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠ABE+∠AEB=90°,
∵BE⊥EF,
∴∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF,
∴=,
∴=,
解得:DF=3.
26.m为何值时,关于x的方程
+=会产生增根?
【考点】分式方程的增根.
【分析】先去分母得2(x+2)+mx=3(x﹣2),整理得(m﹣1)x+10=0,由于关于x的方程
+=会产生增根,则(x+2)(x﹣2)=0,解得x=﹣2
或x=2,然后把x=﹣2
和x=2分别代入(m﹣1)x+10=0即可得到m的值.
【解答】解:原方程化为+=,
方程两边同时乘以(x+2)(x﹣2)
得2(x+2)+mx=3(x﹣2),
整理得(m﹣1)x+10=0,
∵关于x的方程
+=会产生增根,
∴(x+2)(x﹣2)=0,
∴x=﹣2
或x=2,
∴当x=﹣2时,(m﹣1)×(﹣2)+10=0,解得m=6,
当x=2时,(m﹣1)×2+10=0,解得m=﹣4,
∴m=﹣4或m=6时,原方程会产生增根.
27.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设AD=x,FG=y,求y关于x的函数解析式;
(3)在点E、F移动过程中,△AED与△CEF能否相似?若能,求AD的长;若不能,请说明理由.
【考点】相似形综合题.
【分析】(1)由△ADE∽△ACB,得=,由此即可解决问题.
(2)由△BGF∽△BCA,得=,由此即可解决问题.
(3)分两种情形①当∠A=∠CEF时,△ADE∽△ECF,
=.②当∠A=∠CFE时,△ADE∽△FCE,
=,分别列出方程即可解决问题.
【解答】解:(1)∵∠ACB=90°,AB=10,AC=6
∴BC=8∵ED⊥AB,
∴∠ADE=∠ACB=90°
又∵∠A=∠A,
∴△ADE∽△ACB,
∴=,
∴=,
∴DE=4.
(2)∵FG⊥AB,
∴∠BGF=∠BCA=90°,
又∵∠B=∠B,
∴△BGF∽△BCA,
∴=,
∴=,
∴y=﹣x+6.
(3)由(1)(2)可得:AE=x,BF=10﹣x,
∴CE=6﹣x,CF=x﹣2,
当∠A=∠CEF时,△ADE∽△ECF,
∴=.
∴=,
解得:x=;
当∠A=∠CFE时,△ADE∽△FCE,
∴=,
∴=,
解得:,
∴当AD的长为或时△AED与△CEF相似.
2016年11月29日
第1页(共17页)
同课章节目录
