14.2.1平方差公式课件

课件15张PPT。14.2.1平方差公式计算下列多项式的积.你能发现什么规律?（1）（2）（3）1.等式左边相乘的两个多项式有什么共同特点？=x2-12=m2-22=(2x)2-122.等式右边的各项和左边各项有什么关系？4.你能证明吗？3.你能将发现的规律用式子表示出来吗？【探究】【思考？】你能将平方差公式用文字语言表述吗?平方差公式两个数的和与这两个数的差的积，
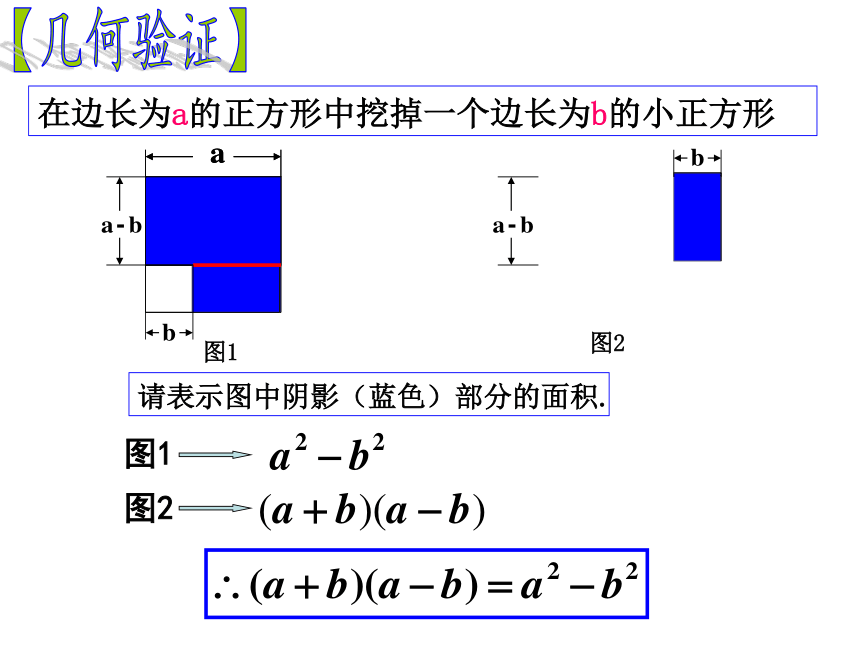
等于这两个数的平方差.你还能用其它方法证明此结论的正确性吗？【代数验证】请表示图中阴影（蓝色）部分的面积.图2图1在边长为a的正方形中挖掉一个边长为b的小正方形【几何验证】这两个数的平方差； (1)公式左边是：两项×两项是相同两数的和与差的积. 第一项相同、第二项符号相反. (2)公式右边是： （第一项）2－（第二项）2【理解公式】｛特征
结构(1) (a+b)(?a?b)
(2) (-2x+y)(y+2x).
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (a?b)(b?a) ;(不能) 1.下列式子可用平方差公式计算吗? (能) (不能) (能) (不能) (a?b)(?a+b)(a+2b)(a+2b)(y-2x)(y+2x)【练习】加法交换律例1：运用平方差公式计算：（1） （2） （3） ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别公式中的两数a, b.【例题解析】【分析】 (1)公式左边是：两项×两项(2)公式右边是： 【重新理解公式】｛特征
结构一项相同、另一项符号相反. （相同项）2－（相反项）2(2) (m +2n) (2n -m) = ( )2 – ( )2试一试： 填空： (1) (5x +2) (5x -2) = ( )2 – ( )2m (3) (-a +2b) (-2b -a) = ( )2 – ( )2 5x22n 2b -a (4) (-1.2y +x) (x +1.2y) = ( )2 – ( )2 x 1.2yy3(1) (2x+3a)(2x-3b)=(2x)2-(3a)2;
(2) (2a-3b)(2a-3b)=(2a)2-(3b)2 ;
(3) (x+2)(x-2)=x2-2;
(4) (-3a?2)(3a-2)=9a2-4 ;
(不对) 2.下列各式的计算对不对？? 如果不对，应当怎样改正? (不对) (不对) =4x2-6bx+6ax-9ab(不对) =4a2-6ab-6ab+9b2=x2-4=(-2)2-(3a)2=4-9a2【练习】=4a2-12ab+9b2例2：计算：（1） （2） 【例题解析】(1) 51×49;
(2) (y+2)(2-y) - (-3-y)(y-3)
(3) (3x+4)(3x-4)-(2x+3)(3x-2) ;3.计算. 【练习】你有几种不同的填法？【拓展升华】（2+1)(22+1)(24+1). (2+1)(22+1)(24+1) … (22n+1)= 24n-1 解：原式 =(2-1)(2+1)(22+1)(24+1)=(22-1)(22+1)(24+1)=(24-1)(24+1)=28-1【课堂小结】1.本节课学了哪些主要内容？2. 平方差公式的结构特征是什么？3. 应用平方差公式是要注意什么？再见【作业】作业本1，原创A