黑龙江省哈尔滨市第四十一中学2016-2017学年七年级(五四制)9月月考数学试题(答案不全)
文档属性
| 名称 | 黑龙江省哈尔滨市第四十一中学2016-2017学年七年级(五四制)9月月考数学试题(答案不全) |  | |
| 格式 | zip | ||
| 文件大小 | 57.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-30 18:02:57 | ||
图片预览

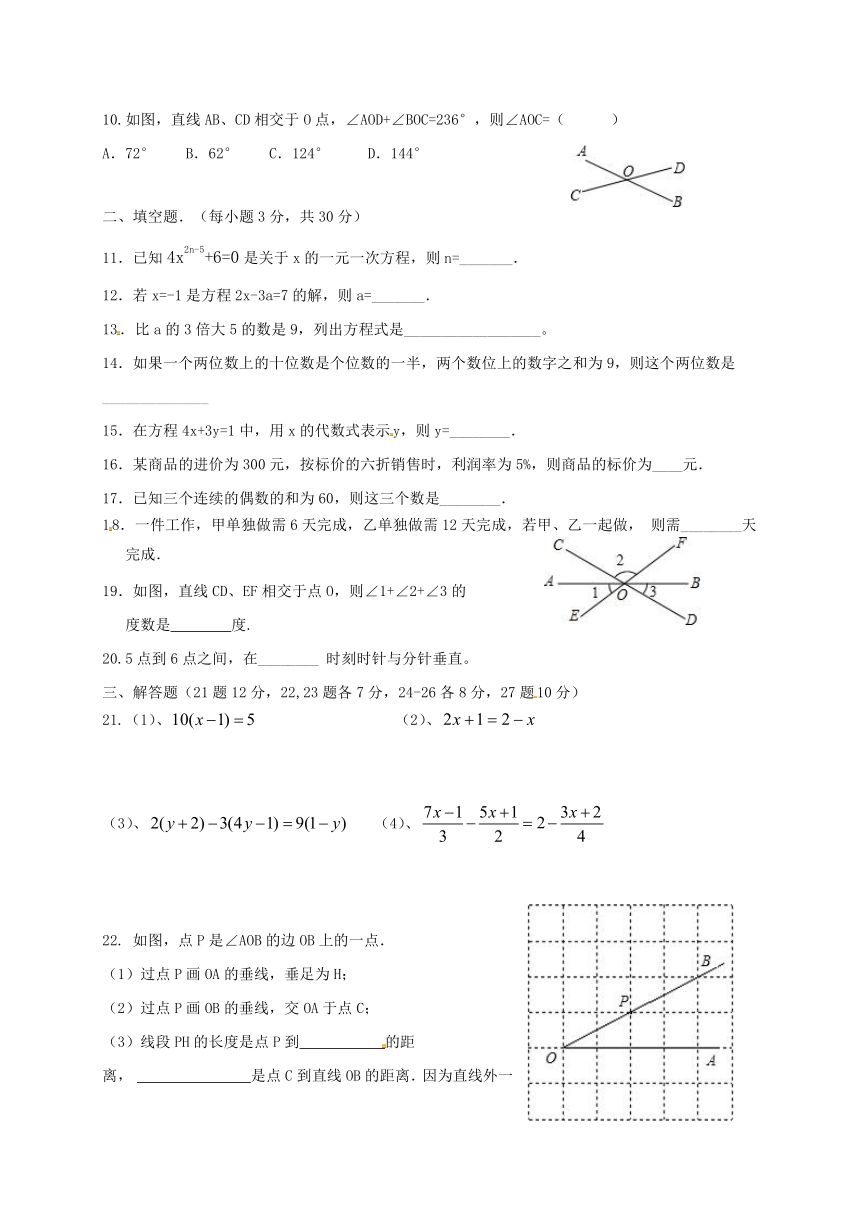
文档简介
2016年哈尔滨是第四十一中学校七年级数学9月月考试题
一、选择题(每小题3分,共30分)
1.下列方程中,属于一元一次方程的是( )
A.
B.
C
D.
2.已知ax
=
ay,下列等式中成立的是(
)
A.x
=
y
B.ax
+
1
=
ay
-
1
C.
ax
=
-
ay
D.3
-
ax
=
3
-
ay
3.一件商品提价25%后发现销路不是很好,欲恢复原价,则应降价(
)
A.40%
B.20%
C
25%
D.15%
4.一列长a米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程是(
)
A.a米
B.(a+60)米
C.60a米 D.(60+2a
)米
5.解方程时,把分母化为整数,得
(
)。
A、
B、
C、
D、
6.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(
)
A.相等
B.互余
C.互补
D.互为对顶角
7.把一捆书分给一个课外小组的每位同学,如果每人5本,那么剩
4本书,如果每人6本,那么刚好最后一人无书可领,
这捆书的本数是(
)
A.10
B.52
C.54 D.56
8.一条山路,某人从山下往山顶走3小时还有1千米才到山顶,若从山顶走到山下只用150分钟,已知下山速度是上山速度的1.5倍,求山下到山顶的路程.设上山速度为x千米/分钟,则所列方程为(
)
A.x-1=5(1.5x)
B.3x+1=50(1.5x)
C.3x-1=
(1.5x)
D.180x+1=150(1.5x)
9.某商品的进货价为每件x元,零售价为每件900元,为了适应市场竞争,商店按零售价的九折让利40元销售,仍可获利10%,则x为( )
A.约700元
B.约773元
C.约736元 D.约865元
10.如图,直线AB、CD相交于O点,∠AOD+∠BOC=236°,则∠AOC=(
)
A.72°
B.62°
C.124°
D.144°
二、填空题.(每小题3分,共30分)
11.已知4x2n-5+6=0是关于x的一元一次方程,则n=_______.
12.若x=-1是方程2x-3a=7的解,则a=_______.
13.比a的3倍大5的数是9,列出方程式是__________________。
14.如果一个两位数上的十位数是个位数的一半,两个数位上的数字之和为9,则这个两位数是______________
15.在方程4x+3y=1中,用x的代数式表示y,则y=________.
16.某商品的进价为300元,按标价的六折销售时,利润率为5%,则商品的标价为____元.
17.已知三个连续的偶数的和为60,则这三个数是________.
18.一件工作,甲单独做需6天完成,乙单独做需12天完成,若甲、乙一起做,则需________天完成.
19.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的
度数是
度.
20.5点到6点之间,在________
时刻时针与分针垂直。
三、解答题(21题12分,22,23题各7分,24-26各8分,27题10分)
21.(1)、
(2)、
(3)、
(4)、
22.
如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)线段PH的长度是点P到
的距
离,
是点C到直线OB的距离.因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是
.(用“<”号连接)
23.
y=1是方程的解,求关于x的方程的解。
24.
一艘船在两个码头之间航行,水流的速度是3千米/时,顺水航行需要2小时,逆水航行需要3小时,求两码头之间的距离。
25.
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=∠BOC,求∠AOC与∠MOD.
26.
张老师带领该校七年级"三好学生"去开展夏令营活动,甲旅行社说:"如果老师买全票一张,则学生可享受半价优惠。"乙旅行社说:"包括老师在内按全票价的6折优惠。"若全票价为240元,当学生人数为多少人时,两家旅行社的收费一样多?
27.与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。
⑴
行人的速度为每秒多少米?
⑵
这列火车的车长是多少米?
7年9月月考选择答案
1—5
CDBBB
6—10
BCDAB
一、选择题(每小题3分,共30分)
1.下列方程中,属于一元一次方程的是( )
A.
B.
C
D.
2.已知ax
=
ay,下列等式中成立的是(
)
A.x
=
y
B.ax
+
1
=
ay
-
1
C.
ax
=
-
ay
D.3
-
ax
=
3
-
ay
3.一件商品提价25%后发现销路不是很好,欲恢复原价,则应降价(
)
A.40%
B.20%
C
25%
D.15%
4.一列长a米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程是(
)
A.a米
B.(a+60)米
C.60a米 D.(60+2a
)米
5.解方程时,把分母化为整数,得
(
)。
A、
B、
C、
D、
6.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(
)
A.相等
B.互余
C.互补
D.互为对顶角
7.把一捆书分给一个课外小组的每位同学,如果每人5本,那么剩
4本书,如果每人6本,那么刚好最后一人无书可领,
这捆书的本数是(
)
A.10
B.52
C.54 D.56
8.一条山路,某人从山下往山顶走3小时还有1千米才到山顶,若从山顶走到山下只用150分钟,已知下山速度是上山速度的1.5倍,求山下到山顶的路程.设上山速度为x千米/分钟,则所列方程为(
)
A.x-1=5(1.5x)
B.3x+1=50(1.5x)
C.3x-1=
(1.5x)
D.180x+1=150(1.5x)
9.某商品的进货价为每件x元,零售价为每件900元,为了适应市场竞争,商店按零售价的九折让利40元销售,仍可获利10%,则x为( )
A.约700元
B.约773元
C.约736元 D.约865元
10.如图,直线AB、CD相交于O点,∠AOD+∠BOC=236°,则∠AOC=(
)
A.72°
B.62°
C.124°
D.144°
二、填空题.(每小题3分,共30分)
11.已知4x2n-5+6=0是关于x的一元一次方程,则n=_______.
12.若x=-1是方程2x-3a=7的解,则a=_______.
13.比a的3倍大5的数是9,列出方程式是__________________。
14.如果一个两位数上的十位数是个位数的一半,两个数位上的数字之和为9,则这个两位数是______________
15.在方程4x+3y=1中,用x的代数式表示y,则y=________.
16.某商品的进价为300元,按标价的六折销售时,利润率为5%,则商品的标价为____元.
17.已知三个连续的偶数的和为60,则这三个数是________.
18.一件工作,甲单独做需6天完成,乙单独做需12天完成,若甲、乙一起做,则需________天完成.
19.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的
度数是
度.
20.5点到6点之间,在________
时刻时针与分针垂直。
三、解答题(21题12分,22,23题各7分,24-26各8分,27题10分)
21.(1)、
(2)、
(3)、
(4)、
22.
如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)线段PH的长度是点P到
的距
离,
是点C到直线OB的距离.因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是
.(用“<”号连接)
23.
y=1是方程的解,求关于x的方程的解。
24.
一艘船在两个码头之间航行,水流的速度是3千米/时,顺水航行需要2小时,逆水航行需要3小时,求两码头之间的距离。
25.
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=∠BOC,求∠AOC与∠MOD.
26.
张老师带领该校七年级"三好学生"去开展夏令营活动,甲旅行社说:"如果老师买全票一张,则学生可享受半价优惠。"乙旅行社说:"包括老师在内按全票价的6折优惠。"若全票价为240元,当学生人数为多少人时,两家旅行社的收费一样多?
27.与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。
⑴
行人的速度为每秒多少米?
⑵
这列火车的车长是多少米?
7年9月月考选择答案
1—5
CDBBB
6—10
BCDAB
同课章节目录
