鲁教版(五四学制)七年级上3.1探索勾股定理(1)同步测试含答案解析
文档属性
| 名称 | 鲁教版(五四学制)七年级上3.1探索勾股定理(1)同步测试含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 06:29:45 | ||
图片预览

文档简介
知能提升作业(十五)
第三章 勾股定理
1 探索勾股定理
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图,现有一长方形公园ABCD,如果游人要从景点A走到景点C,则至少走( )
(A)200米
(B)250米
(C)600米
(D)800米
2.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
(A)2
(B)4
(C)9
(D)16
3.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
(A)600m
(B)500m
(C)400m
(D)300m
二、填空题(每小题4分,共12分)
4.在直角三角形ABC中,∠C=90°,BC=12,AC=9,则AB=________.
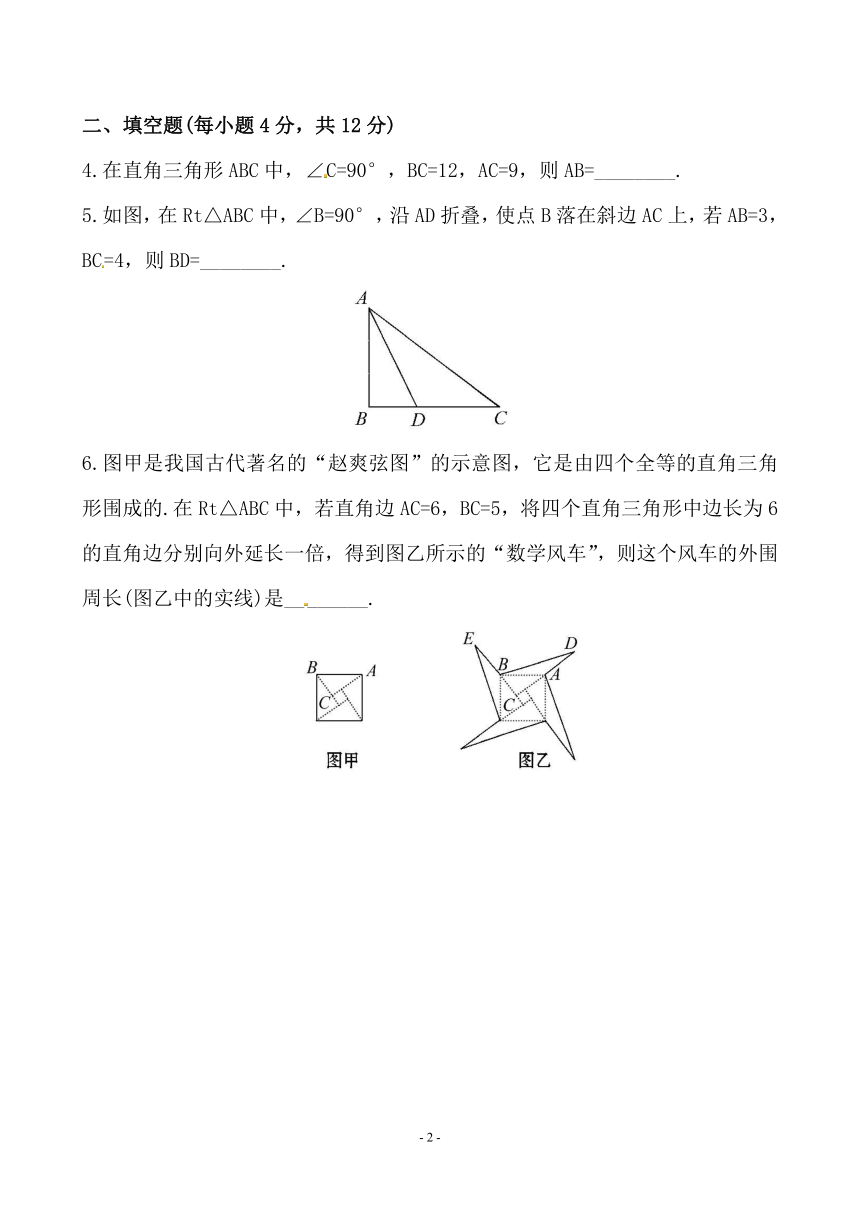
5.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=________.
6.图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是________.
三、解答题(共26分)
7.
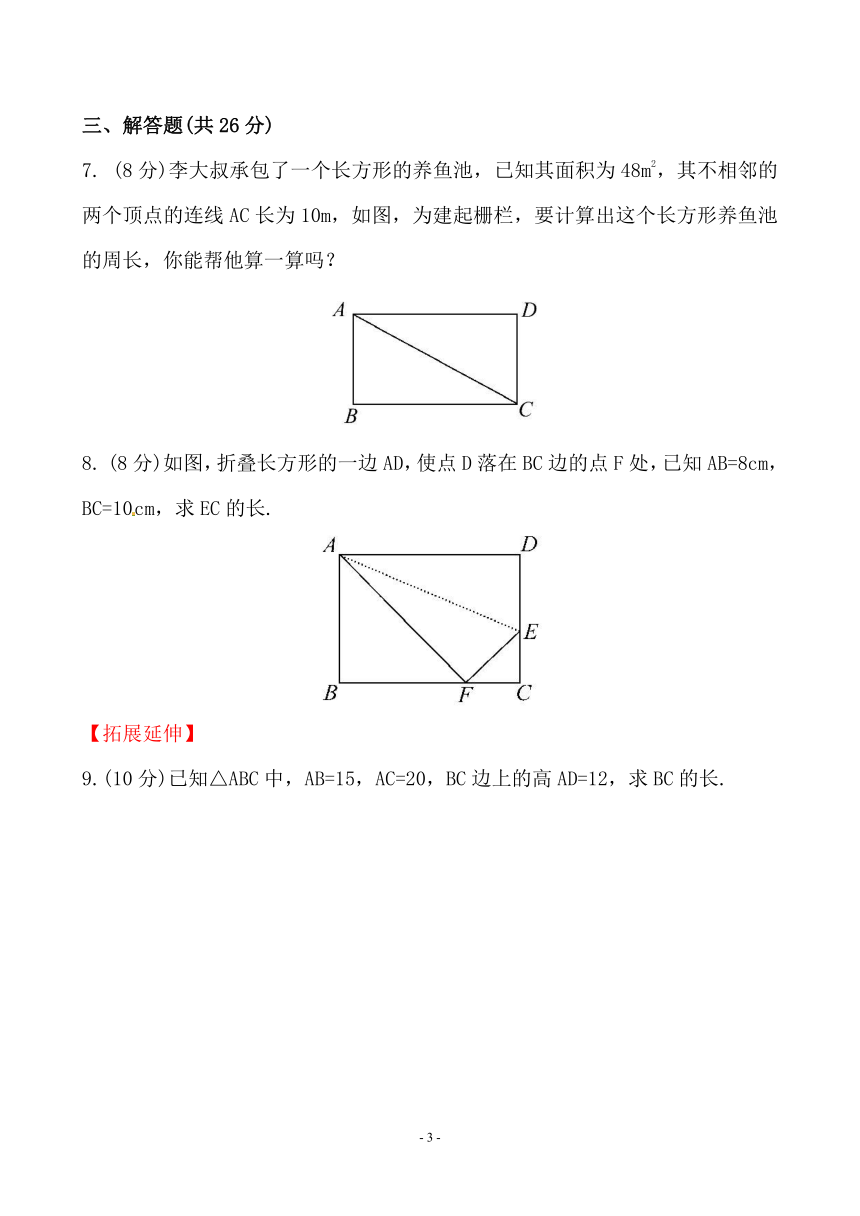
(8分)李大叔承包了一个长方形的养鱼池,已知其面积为48m2,其不相邻的两个顶点的连线AC长为10m,如图,为建起栅栏,要计算出这个长方形养鱼池的周长,你能帮他算一算吗?
8.
(8分)如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
【拓展延伸】
9.(10分)已知△ABC中,AB=15,AC=20,BC边上的高AD=12,求BC的长.
答案解析
1.【解析】选B.从景点A走到景点C的最短距离为AC,
在直角△ACD中,因为AC2=AD2+CD2=2002+1502=62500,
所以AC=250米.
2.【解析】选A.由勾股定理得
AE2=DE2+AD2
=DE2+CD2+AC2
=DE2+CD2+BC2+AB2
=1+1+1+1=4=22,
故AE=2.
3.【解析】选B.小明去书店共有三种走法:
(1)A→C→书店;
(2)A→B→书店;
(3)A→B→D→书店.
因为曙光路与环城路垂直,
所以△BDE为直角三角形,所以BD>BE,
所以(3)的路程大于(2)的路程,
因此只比较(1)、(2)的路程即可.
在△ABC和△EDB中,
因为∠CAB=∠BED=90°,AC∥BD,∠ACB=∠EBD,AB=ED,所以△ABC≌△EDB,
所以BE=AC=300m,由勾股定理得BC=500m,
所以EC=500-300=200(m),
所以(1)的路程为:300+200=500(m);
(2)的路程为:400+300=700(m),
所以(1)的路程最短,为500m,故选B.
4.【解析】在直角三角形ABC中,由勾股定理可得AB=15.
答案:15
5.【解析】设B点的对应点为B′,连接DB′,
由勾股定理得AC=5,又AB′=AB,
所以B′C=5-3=2,
设DB=DB′=x,则DC=4-x.
在Rt△DB′C中,利用勾股定理得x2+22=(4-x)2,
解得x=,即BD=.
答案:
6.【解析】因为BD2=122+52=132,BE=6,
所以风车的外围周长=4×(13+6)=76.
答案:76
7.【解析】设长方形中,BC=x,AB=y,根据题意得
由②可得(x+y)2-2xy=100 ③
将①代入③得x+y=±14(负值舍去),
所以2(x+y)=2×14=28(m),
所以长方形养鱼池的周长为28m.
8.【解析】设EC=xcm,则DE=(8-x)cm,由折叠可知,EF=DE,AD=AF,
在直角△ABF中,由勾股定理得AB2+BF2=AF2,
即82+BF2=102,所以BF=6cm,
所以FC=10-6=4(cm).
在直角△EFC中,由勾股定理得FC2+CE2=EF2,即
42+x2=(8-x)2,解之得x=3,
即EC的长度为3cm.
9.【解析】本题应分两种情况:
①当AD在三角形内部时,如图(1)
在直角△ADB和直角△ADC中,由勾股定理得
BD2=AB2-AD2=152-122=81,
CD2=AC2-AD2=202-122=256,
所以BD=9,CD=16,
所以BC=BD+CD=9+16=25.
②当AD在三角形外部时,如图(2)
由勾股定理得
CD2=AC2-AD2=202-122
=256,
BD2=AB2-AD2=152-122
=81,
所以CD=16,BD=9,
所以BC=CD-BD=16-9=7.
综上所述,BC的长为25或7.
PAGE
-
1
-
第三章 勾股定理
1 探索勾股定理
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图,现有一长方形公园ABCD,如果游人要从景点A走到景点C,则至少走( )
(A)200米
(B)250米
(C)600米
(D)800米
2.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
(A)2
(B)4
(C)9
(D)16
3.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
(A)600m
(B)500m
(C)400m
(D)300m
二、填空题(每小题4分,共12分)
4.在直角三角形ABC中,∠C=90°,BC=12,AC=9,则AB=________.
5.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=________.
6.图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是________.
三、解答题(共26分)
7.
(8分)李大叔承包了一个长方形的养鱼池,已知其面积为48m2,其不相邻的两个顶点的连线AC长为10m,如图,为建起栅栏,要计算出这个长方形养鱼池的周长,你能帮他算一算吗?
8.
(8分)如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
【拓展延伸】
9.(10分)已知△ABC中,AB=15,AC=20,BC边上的高AD=12,求BC的长.
答案解析
1.【解析】选B.从景点A走到景点C的最短距离为AC,
在直角△ACD中,因为AC2=AD2+CD2=2002+1502=62500,
所以AC=250米.
2.【解析】选A.由勾股定理得
AE2=DE2+AD2
=DE2+CD2+AC2
=DE2+CD2+BC2+AB2
=1+1+1+1=4=22,
故AE=2.
3.【解析】选B.小明去书店共有三种走法:
(1)A→C→书店;
(2)A→B→书店;
(3)A→B→D→书店.
因为曙光路与环城路垂直,
所以△BDE为直角三角形,所以BD>BE,
所以(3)的路程大于(2)的路程,
因此只比较(1)、(2)的路程即可.
在△ABC和△EDB中,
因为∠CAB=∠BED=90°,AC∥BD,∠ACB=∠EBD,AB=ED,所以△ABC≌△EDB,
所以BE=AC=300m,由勾股定理得BC=500m,
所以EC=500-300=200(m),
所以(1)的路程为:300+200=500(m);
(2)的路程为:400+300=700(m),
所以(1)的路程最短,为500m,故选B.
4.【解析】在直角三角形ABC中,由勾股定理可得AB=15.
答案:15
5.【解析】设B点的对应点为B′,连接DB′,
由勾股定理得AC=5,又AB′=AB,
所以B′C=5-3=2,
设DB=DB′=x,则DC=4-x.
在Rt△DB′C中,利用勾股定理得x2+22=(4-x)2,
解得x=,即BD=.
答案:
6.【解析】因为BD2=122+52=132,BE=6,
所以风车的外围周长=4×(13+6)=76.
答案:76
7.【解析】设长方形中,BC=x,AB=y,根据题意得
由②可得(x+y)2-2xy=100 ③
将①代入③得x+y=±14(负值舍去),
所以2(x+y)=2×14=28(m),
所以长方形养鱼池的周长为28m.
8.【解析】设EC=xcm,则DE=(8-x)cm,由折叠可知,EF=DE,AD=AF,
在直角△ABF中,由勾股定理得AB2+BF2=AF2,
即82+BF2=102,所以BF=6cm,
所以FC=10-6=4(cm).
在直角△EFC中,由勾股定理得FC2+CE2=EF2,即
42+x2=(8-x)2,解之得x=3,
即EC的长度为3cm.
9.【解析】本题应分两种情况:
①当AD在三角形内部时,如图(1)
在直角△ADB和直角△ADC中,由勾股定理得
BD2=AB2-AD2=152-122=81,
CD2=AC2-AD2=202-122=256,
所以BD=9,CD=16,
所以BC=BD+CD=9+16=25.
②当AD在三角形外部时,如图(2)
由勾股定理得
CD2=AC2-AD2=202-122
=256,
BD2=AB2-AD2=152-122
=81,
所以CD=16,BD=9,
所以BC=CD-BD=16-9=7.
综上所述,BC的长为25或7.
PAGE
-
1
-
