鲁教版(五四学制)七年级上3.1探索勾股定理(2)同步测试含答案解析
文档属性
| 名称 | 鲁教版(五四学制)七年级上3.1探索勾股定理(2)同步测试含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 07:01:31 | ||
图片预览


文档简介
知能提升作业(十六)
第2课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
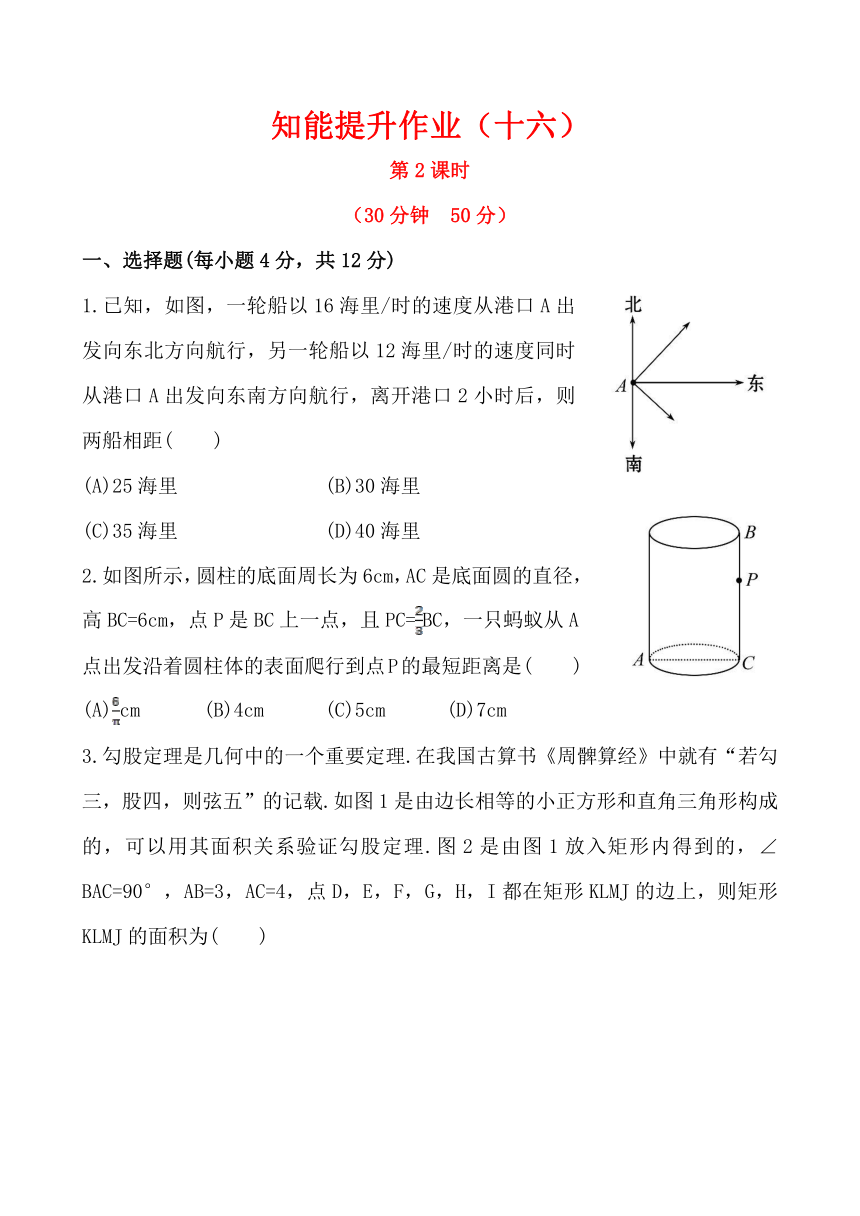
1.已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
(A)25海里
(B)30海里
(C)35海里
(D)40海里
2.如图所示,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是BC上一点,且PC=BC,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
(A)cm
(B)4cm
(C)5cm
(D)7cm
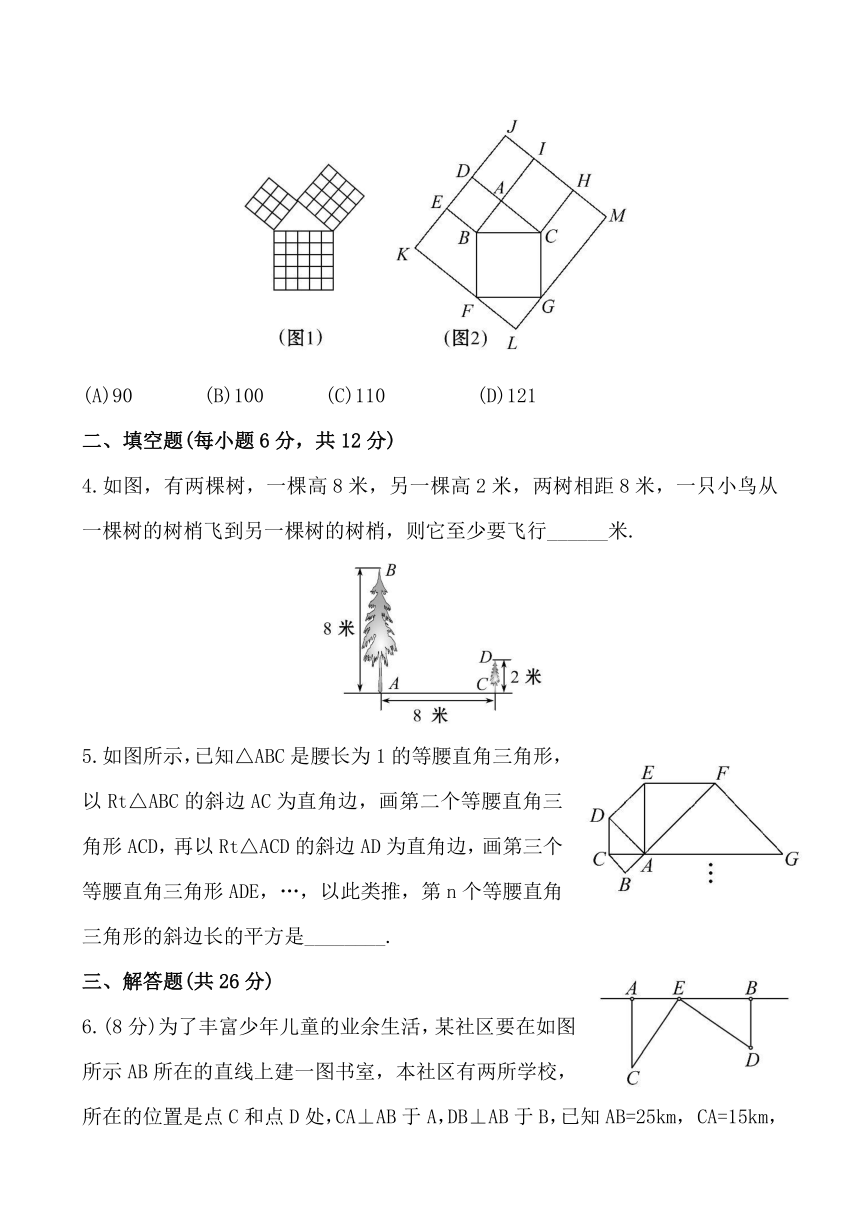
3.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
( http: / / www.21cnjy.com )
(A)90
(B)100
(C)110
(D)121
二、填空题(每小题6分,共12分)
4.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行______米.
( http: / / www.21cnjy.com )
5.如图所示,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,以此类推,第n个等腰直角三角形的斜边长的平方是________.
三、解答题(共26分)
6.(8分)为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置是点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,
CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
7.(8分)如图所示,隔湖有两点A,B,
( http: / / www.21cnjy.com )在与BA方向成直角的BC上的C点,测得CA=50米,CB=40米.求:(1)A,B两点的距离.(2)请求出B点到直线AC的最短距离.
【拓展延伸】
8.(10分)如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度沿BC方向移动,已知城市A到BC的最短距离AD=90km.
(1)台风中心经过多长时间从B点移到D点?
(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,游人必须在接到台风警报后的几小时内撤离(撤离速度为6km/h),最好选择什么方向?
答案解析
1.【解析】选D.两小时后,两艘船分别行驶
( http: / / www.21cnjy.com )了16×2=32(海里),12×2=24(海里),设两小时后两船相距x海里,根据勾股定理得:x2=322+242=402,x=40.故选D.
2.【解析】选C.如图为圆柱的侧面展开图,AP即为所求的最短距离,因为圆柱的底面周长为6cm,所以AA′=6cm,所以AC=3cm,又因为PC=BC=×6=4(cm).在Rt△APC中,AP2=AC2+CP2=32+42,所以AP=5cm.
3.【解析】选C.如图,过B作BN⊥KL于
( http: / / www.21cnjy.com )N.则△BNF≌△CAB.所以BN=AC=4,NF=AB=3,同理FL=4.所以KL=KN+NF+FL=10,KJ=KE+ED+DJ=11,所以矩形KLMJ的面积为10×11=110.
( http: / / www.21cnjy.com )
4.【解析】如图,连接BD,作DH⊥AB交AB于H,
则DH=AC=8米,
BH=AB-AH
=8-2=6(米),
在直角三角形BDH中,BD2=BH2+DH2=62+82=100,
所以BD=10米,即小鸟至少要飞行10米.
答案:10
5.【解析】第一个等腰直角
( http: / / www.21cnjy.com )三角形的斜边长的平方等于2,第2个等腰直角三角形的斜边长的平方等于4,第3个等腰直角三角形的斜边长的平方等于8,…,故第n个等腰直角三角形的斜边长的平方等于2n.
答案:2n
6.【解析】设AE=xkm,则BE=(25-x)km;
在Rt△ACE中,由勾股定理得:
CE2=AE2+AC2=x2+152;
同理可得:DE2=(25-x)2+102;
若CE=DE,则x2+152=(25-x)2+102;
解得:x=10.
答:图书室E应建在A,B之间,距离A点10km处.
7.【解析】(1)由题意知△ABC是直角三角形,由勾股定理可知AC2=BC2+AB2,
又AC=50米,BC=40米,于是AB2=502-402=900,
所以AB=30米.
(2)过点B作BD⊥AC,垂足为D.
△ABC的面积=AB×BC
=AC×BD,
则AB×BC=AC×BD
所以BD====24(米).
答:(1)A,B两点的距离为30米.(2)B点到AC的最短距离为24米.
8.【解析】(1)在直角三角形ABD中,
根据勾股定理,得BD2=1502-902,
故得,BD=120(km).
120÷20=6(h).
即台风中心经过6小时从B点移到D点.
(2)根据题意,可得游人最好选择沿射线DA方向撤离.
撤离的时间为:30÷6=5(时).
又台风到点D的时间是6小时,
即游人必须在接到台风警报后的1小时内撤离,最好选择射线DA方向.
第2课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
(A)25海里
(B)30海里
(C)35海里
(D)40海里
2.如图所示,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是BC上一点,且PC=BC,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
(A)cm
(B)4cm
(C)5cm
(D)7cm
3.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
( http: / / www.21cnjy.com )
(A)90
(B)100
(C)110
(D)121
二、填空题(每小题6分,共12分)
4.如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行______米.
( http: / / www.21cnjy.com )
5.如图所示,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,以此类推,第n个等腰直角三角形的斜边长的平方是________.
三、解答题(共26分)
6.(8分)为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置是点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,
CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
7.(8分)如图所示,隔湖有两点A,B,
( http: / / www.21cnjy.com )在与BA方向成直角的BC上的C点,测得CA=50米,CB=40米.求:(1)A,B两点的距离.(2)请求出B点到直线AC的最短距离.
【拓展延伸】
8.(10分)如图,某沿海城市A接到台风警报,在该市正南方向150km的B处有一台风中心正以20km/h的速度沿BC方向移动,已知城市A到BC的最短距离AD=90km.
(1)台风中心经过多长时间从B点移到D点?
(2)如果在距台风中心30km的圆形区域内都有受到台风破坏的危险,为让D点的游人脱离危险,游人必须在接到台风警报后的几小时内撤离(撤离速度为6km/h),最好选择什么方向?
答案解析
1.【解析】选D.两小时后,两艘船分别行驶
( http: / / www.21cnjy.com )了16×2=32(海里),12×2=24(海里),设两小时后两船相距x海里,根据勾股定理得:x2=322+242=402,x=40.故选D.
2.【解析】选C.如图为圆柱的侧面展开图,AP即为所求的最短距离,因为圆柱的底面周长为6cm,所以AA′=6cm,所以AC=3cm,又因为PC=BC=×6=4(cm).在Rt△APC中,AP2=AC2+CP2=32+42,所以AP=5cm.
3.【解析】选C.如图,过B作BN⊥KL于
( http: / / www.21cnjy.com )N.则△BNF≌△CAB.所以BN=AC=4,NF=AB=3,同理FL=4.所以KL=KN+NF+FL=10,KJ=KE+ED+DJ=11,所以矩形KLMJ的面积为10×11=110.
( http: / / www.21cnjy.com )
4.【解析】如图,连接BD,作DH⊥AB交AB于H,
则DH=AC=8米,
BH=AB-AH
=8-2=6(米),
在直角三角形BDH中,BD2=BH2+DH2=62+82=100,
所以BD=10米,即小鸟至少要飞行10米.
答案:10
5.【解析】第一个等腰直角
( http: / / www.21cnjy.com )三角形的斜边长的平方等于2,第2个等腰直角三角形的斜边长的平方等于4,第3个等腰直角三角形的斜边长的平方等于8,…,故第n个等腰直角三角形的斜边长的平方等于2n.
答案:2n
6.【解析】设AE=xkm,则BE=(25-x)km;
在Rt△ACE中,由勾股定理得:
CE2=AE2+AC2=x2+152;
同理可得:DE2=(25-x)2+102;
若CE=DE,则x2+152=(25-x)2+102;
解得:x=10.
答:图书室E应建在A,B之间,距离A点10km处.
7.【解析】(1)由题意知△ABC是直角三角形,由勾股定理可知AC2=BC2+AB2,
又AC=50米,BC=40米,于是AB2=502-402=900,
所以AB=30米.
(2)过点B作BD⊥AC,垂足为D.
△ABC的面积=AB×BC
=AC×BD,
则AB×BC=AC×BD
所以BD====24(米).
答:(1)A,B两点的距离为30米.(2)B点到AC的最短距离为24米.
8.【解析】(1)在直角三角形ABD中,
根据勾股定理,得BD2=1502-902,
故得,BD=120(km).
120÷20=6(h).
即台风中心经过6小时从B点移到D点.
(2)根据题意,可得游人最好选择沿射线DA方向撤离.
撤离的时间为:30÷6=5(时).
又台风到点D的时间是6小时,
即游人必须在接到台风警报后的1小时内撤离,最好选择射线DA方向.
