鲁教版(五四学制)七年级上5.2平面直角坐标系(1)同步测试含答案解析
文档属性
| 名称 | 鲁教版(五四学制)七年级上5.2平面直角坐标系(1)同步测试含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 526.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 08:33:48 | ||
图片预览


文档简介
知能提升作业(二十七)
2 平面直角坐标系
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.已知M(2+x,9-x2)在x轴的负半轴上,则点M的坐标为( )
(A)(-1,0)
(B)(-3,0)
(C)(0,-3)
(D)(1,1)
2.如图,若在象棋盘上建立直角坐标系,使“”位于点(-1,-2),“”位于点(2,-2),则“”位于点( )
(A)(-1,1)
(B)(-2,-1)
(C)(-3,1)
(D)(1,-2)
3.如图,在平面直角坐标系中,点E的坐标是( )
(A)(1,2)
(B)(2,1)
(C)(-1,2)
(D)(1,-2)
二、填空题(每小题4分,共12分)
4.若点A(a,b)在第三象限,则点B(-a+1,3b-5)在第______象限.
5.若点P(2m-3,m+1)在第一象限的角平分线上,则点P的坐标为________.
6.若|2x-4|+(y-3)2=0,那么点P(x+5,y-1)在第________象限.
三、解答题(共26分)
7.(8分)如图的直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(9,0),C(7,5),D(2,7),试确定这个四边形的面积.
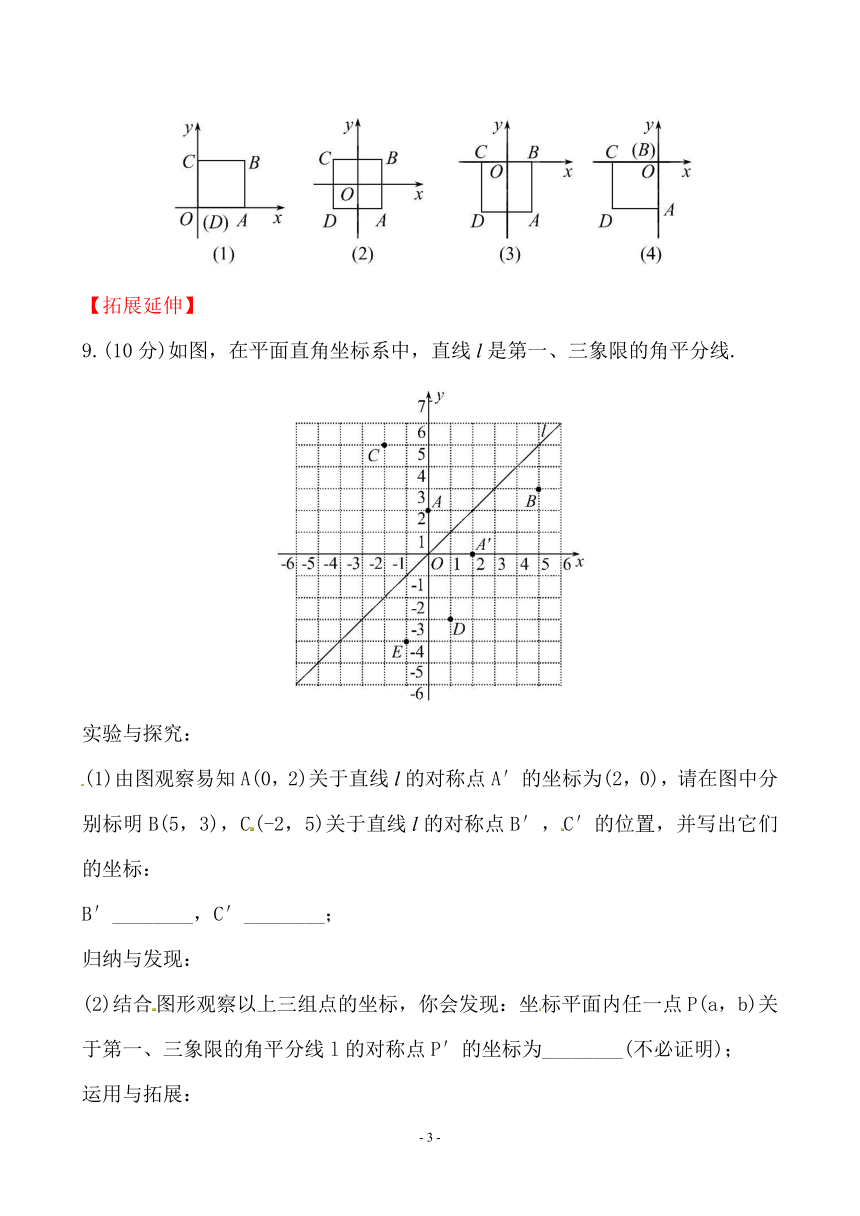
8.(8分)已知正方形ABCD的边长为4,它在坐标系内的位置如图所示,请分别求出下列情况下四个顶点的坐标.
【拓展延伸】
9.(10分)如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3),C(-2,5)关于直线l的对称点B′,C′的位置,并写出它们的坐标:
B′________,C′________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为________(不必证明);
运用与拓展:
(3)已知两点D(1,-3),E(-1,-4),试在直线l上确定一点Q,使点Q到D,E两点的距离之和最小.
答案解析
1.【解析】选A.由题意知2+x<0且9-x2=0,可得x=-3,因此点M坐标为(-1,0).
2.【解析】选C.如图,根据“”位于点(-1,-2)推知“”位于(0,0)处,以“”的位置可以验证推断正确,因此可知“”的位置为(-3,1).
3.【解析】选A.过点E向x轴画垂线,垂足在x轴上对应的实数是1,因此点E的横坐标为1;同理,过点E向y轴画垂线,对应的实数是2,则点E的纵坐标为2,所以点E的坐标为(1,2).
4.【解析】因为点A(a,b)在第三象限,则有a<0,b<0,所以-a+1>0,3b-5<0,所以点B(-a+1,3b-5)在第四象限.
答案:四
5.【解析】第一象限的角平分线上的点横、纵坐标相等,且都为正值.P点在第一象限的角平分线上,则有2m-3=m+1,解得m=4,则P点的坐标为(5,5).
答案:(5,5)
6.【解析】根据非负数原则可知
求出x=2,y=3.
所以x+5=2+5=7>0,y-1=3-1=2>0,
故知点P是第一象限的点.
答案:一
7.【解析】分别过点D,C向x轴作垂线,垂足分别为E,F,如图.
则四边形ABCD被分割成△AED,△BCF和梯形CDEF.由各点的坐标可得AE=2,DE=7,EF=5,FB=2,CF=5.
所以S四边形ABCD=S△AED+S梯形CDEF+S△BCF
=×2×7+×(7+5)×5+×5×2
=7+30+5=42.
【归纳整合】
1.求不规则图形的面积
将不规则图形分割为n个规则图形是求不规则图形面积的一种常用方法.
2.将点的坐标转化为距离
由点的坐标的意义知,横坐标的绝对值是点到y轴的距离,纵坐标的绝对值是点到x轴的距离.
8.【解析】(1)A(4,0),B(4,4),C(0,4),D(0,0).
(2)A(2,-2),B(2,2),C(-2,2),D(-2,-2).
(3)A(2,-4),B(2,0),C(-2,0),D(-2,-4).
(4)A(0,-4),B(0,0),C(-4,0),D(-4,-4).
9.【解析】(1)如图:B′(3,5),C′(5,-2).
(2)(b,a).
(3)由(2)得,D(1,-3)关于直线l的对称点D′的坐标为(-3,1),连接D′E交直线l于点Q,此时点Q到D,E两点的距离之和最小.
PAGE
-
1
-
2 平面直角坐标系
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.已知M(2+x,9-x2)在x轴的负半轴上,则点M的坐标为( )
(A)(-1,0)
(B)(-3,0)
(C)(0,-3)
(D)(1,1)
2.如图,若在象棋盘上建立直角坐标系,使“”位于点(-1,-2),“”位于点(2,-2),则“”位于点( )
(A)(-1,1)
(B)(-2,-1)
(C)(-3,1)
(D)(1,-2)
3.如图,在平面直角坐标系中,点E的坐标是( )
(A)(1,2)
(B)(2,1)
(C)(-1,2)
(D)(1,-2)
二、填空题(每小题4分,共12分)
4.若点A(a,b)在第三象限,则点B(-a+1,3b-5)在第______象限.
5.若点P(2m-3,m+1)在第一象限的角平分线上,则点P的坐标为________.
6.若|2x-4|+(y-3)2=0,那么点P(x+5,y-1)在第________象限.
三、解答题(共26分)
7.(8分)如图的直角坐标系中,四边形ABCD各顶点的坐标分别是A(0,0),B(9,0),C(7,5),D(2,7),试确定这个四边形的面积.
8.(8分)已知正方形ABCD的边长为4,它在坐标系内的位置如图所示,请分别求出下列情况下四个顶点的坐标.
【拓展延伸】
9.(10分)如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3),C(-2,5)关于直线l的对称点B′,C′的位置,并写出它们的坐标:
B′________,C′________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为________(不必证明);
运用与拓展:
(3)已知两点D(1,-3),E(-1,-4),试在直线l上确定一点Q,使点Q到D,E两点的距离之和最小.
答案解析
1.【解析】选A.由题意知2+x<0且9-x2=0,可得x=-3,因此点M坐标为(-1,0).
2.【解析】选C.如图,根据“”位于点(-1,-2)推知“”位于(0,0)处,以“”的位置可以验证推断正确,因此可知“”的位置为(-3,1).
3.【解析】选A.过点E向x轴画垂线,垂足在x轴上对应的实数是1,因此点E的横坐标为1;同理,过点E向y轴画垂线,对应的实数是2,则点E的纵坐标为2,所以点E的坐标为(1,2).
4.【解析】因为点A(a,b)在第三象限,则有a<0,b<0,所以-a+1>0,3b-5<0,所以点B(-a+1,3b-5)在第四象限.
答案:四
5.【解析】第一象限的角平分线上的点横、纵坐标相等,且都为正值.P点在第一象限的角平分线上,则有2m-3=m+1,解得m=4,则P点的坐标为(5,5).
答案:(5,5)
6.【解析】根据非负数原则可知
求出x=2,y=3.
所以x+5=2+5=7>0,y-1=3-1=2>0,
故知点P是第一象限的点.
答案:一
7.【解析】分别过点D,C向x轴作垂线,垂足分别为E,F,如图.
则四边形ABCD被分割成△AED,△BCF和梯形CDEF.由各点的坐标可得AE=2,DE=7,EF=5,FB=2,CF=5.
所以S四边形ABCD=S△AED+S梯形CDEF+S△BCF
=×2×7+×(7+5)×5+×5×2
=7+30+5=42.
【归纳整合】
1.求不规则图形的面积
将不规则图形分割为n个规则图形是求不规则图形面积的一种常用方法.
2.将点的坐标转化为距离
由点的坐标的意义知,横坐标的绝对值是点到y轴的距离,纵坐标的绝对值是点到x轴的距离.
8.【解析】(1)A(4,0),B(4,4),C(0,4),D(0,0).
(2)A(2,-2),B(2,2),C(-2,2),D(-2,-2).
(3)A(2,-4),B(2,0),C(-2,0),D(-2,-4).
(4)A(0,-4),B(0,0),C(-4,0),D(-4,-4).
9.【解析】(1)如图:B′(3,5),C′(5,-2).
(2)(b,a).
(3)由(2)得,D(1,-3)关于直线l的对称点D′的坐标为(-3,1),连接D′E交直线l于点Q,此时点Q到D,E两点的距离之和最小.
PAGE
-
1
-
