鲁教版七年级上5.3轴对称与坐标变化同步测试含答案解析
文档属性
| 名称 | 鲁教版七年级上5.3轴对称与坐标变化同步测试含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 444.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 00:00:00 | ||
图片预览


文档简介
知能提升作业(二十九)
3 轴对称与坐标变化
(30分钟
50分)
一、选择题(每小题4分,共12分)
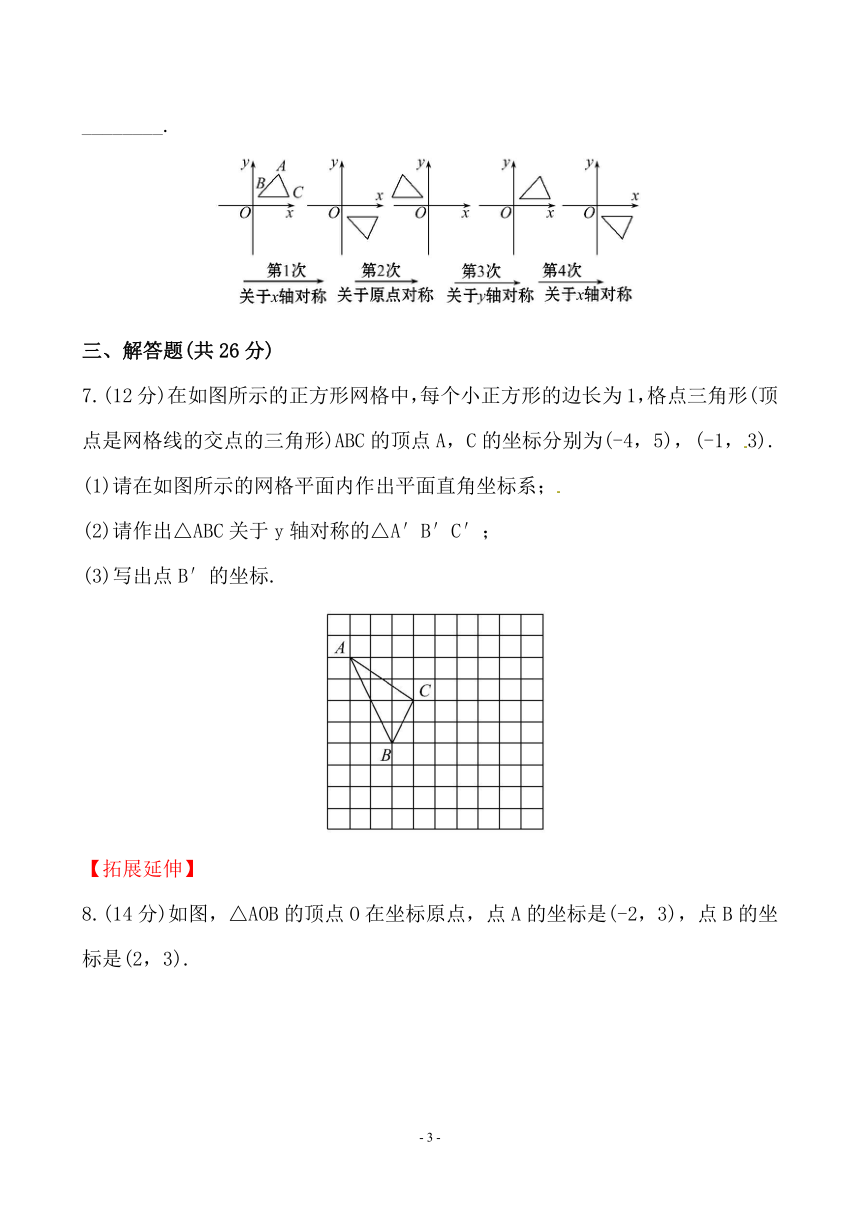
1.线段MN在平面直角坐标系中的位置如图,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
(A)(4,2)
(B)(-4,2)
(C)(-4,-2)
(D)(4,-2)
2.甲、乙两位同学用围棋子做游戏,如图所示,现轮到黑棋下子,黑棋下了后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形,则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
(A)黑(3,7);白(5,3)
(B)黑(4,7);白(6,2)
(C)黑(2,7);白(5,3)
(D)黑(3,7);白(2,6)
3.在平面直角坐标系中,正方形ABCD的顶点坐标分别为A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2013的坐标为( )
(A)(0,2)
(B)(2,0)
(C)(0,-2)
(D)(-2,0)
二、填空题(每小题4分,共12分)
4.点A(-3,-2)关于x轴的对称点为A1,点A1关于y轴的对称点为A2,则A2的坐标为________.
5.已知△ABC与△A′B′C′关于某直线对称,且A,B,C的坐标分别为(-1,-3),(-4,-2)和(-5,0),A′,B′的坐标分别为(-1,3)和(-4,2),则点C的坐标为________.
6.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2013次变换后所得的A点的坐标是________.
三、解答题(共26分)
7.(12分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
【拓展延伸】
8.(14分)如图,△AOB的顶点O在坐标原点,点A的坐标是(-2,3),点B的坐标是(2,3).
(1)写出△AOB关于x轴对称的△A′OB′各顶点的坐标;
(2)将△A′B′O的各顶点坐标都分别乘2后,所得的三角形与原三角形相比,面积如何变化?
答案解析
1.【解析】选D.因为点M的坐标为(-4,-2),所以点M关于y轴对称的点M′的坐标是(4,-2).
2.【解析】选C.A.若放入黑(3,7);白(5,3),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
B.若放入黑(4,7);白(6,2),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
C.若放入黑(2,7);白(5,3),则此时黑棋不是轴对称图形,白棋是轴对称图形,故本选项正确.
D.若放入黑(3,7);白(2,6),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
3.【解析】选B.连接PA并延长交x轴于点P1,因为点A的横、纵坐标相等,所以OA垂直平分线段PP1,则P1(2,0),同理P2(0,-2),P3(-2,0),P4(0,2),由此可见是四个点一循环.又因为2013÷4=503……1,所以点P2013的坐标与点P1(2,0)一样.
4.【解析】因为点A与点A1关于x轴对称,
所以点A1的坐标为(-3,2),
又因为点A1与点A2关于y轴对称,
所以点A2的坐标为(3,2).
答案:(3,2)
5.【解析】根据A与A′,B与B′的坐标关系知,△ABC与△A′B′C′关于x轴对称,故点C的坐标为(-5,0).
答案:(-5,0)
6.【解析】根据题意,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,经过观察图形,动手操作不难发现,每3次为一个周期变换.依次类推第2013次变换相当于2013=671×3次变换,也就是说第2013次变换时已经有671次重复,相当于开始的图形,此时A点的坐标是(a,b).
答案:(a,b)
7.【解析】(1)由A,C两点的坐标就可以确定直角坐标系;
(2)根据轴对称的作图方法,便可作出△ABC关于y轴对称的△A′B′C′;
(3)因为点B的坐标为(-2,1),所以它关于y轴对称的点B′的坐标为(2,1).
8.【解析】(1)△A′OB′各顶点的坐标分别为O(0,0),A′(-2,-3),B′(2,-3).
(2)△OA″B″各顶点的坐标为O(0,0),A″(-4,-6),B″(4,-6),由图可得A′B′=4,OC=3,A″B″=8,OD=6,所以S△A′B′O=×4×3=6.
S△A″B″O=×8×6=24.所以,将△A′B′O各顶点坐标都分别乘2后的三角形面积是△A′B′O的面积的4倍.
PAGE
-
1
-
3 轴对称与坐标变化
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.线段MN在平面直角坐标系中的位置如图,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
(A)(4,2)
(B)(-4,2)
(C)(-4,-2)
(D)(4,-2)
2.甲、乙两位同学用围棋子做游戏,如图所示,现轮到黑棋下子,黑棋下了后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形,则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
(A)黑(3,7);白(5,3)
(B)黑(4,7);白(6,2)
(C)黑(2,7);白(5,3)
(D)黑(3,7);白(2,6)
3.在平面直角坐标系中,正方形ABCD的顶点坐标分别为A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2013的坐标为( )
(A)(0,2)
(B)(2,0)
(C)(0,-2)
(D)(-2,0)
二、填空题(每小题4分,共12分)
4.点A(-3,-2)关于x轴的对称点为A1,点A1关于y轴的对称点为A2,则A2的坐标为________.
5.已知△ABC与△A′B′C′关于某直线对称,且A,B,C的坐标分别为(-1,-3),(-4,-2)和(-5,0),A′,B′的坐标分别为(-1,3)和(-4,2),则点C的坐标为________.
6.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2013次变换后所得的A点的坐标是________.
三、解答题(共26分)
7.(12分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
【拓展延伸】
8.(14分)如图,△AOB的顶点O在坐标原点,点A的坐标是(-2,3),点B的坐标是(2,3).
(1)写出△AOB关于x轴对称的△A′OB′各顶点的坐标;
(2)将△A′B′O的各顶点坐标都分别乘2后,所得的三角形与原三角形相比,面积如何变化?
答案解析
1.【解析】选D.因为点M的坐标为(-4,-2),所以点M关于y轴对称的点M′的坐标是(4,-2).
2.【解析】选C.A.若放入黑(3,7);白(5,3),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
B.若放入黑(4,7);白(6,2),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
C.若放入黑(2,7);白(5,3),则此时黑棋不是轴对称图形,白棋是轴对称图形,故本选项正确.
D.若放入黑(3,7);白(2,6),则此时黑棋是轴对称图形,白棋也是轴对称图形,故本选项错误.
3.【解析】选B.连接PA并延长交x轴于点P1,因为点A的横、纵坐标相等,所以OA垂直平分线段PP1,则P1(2,0),同理P2(0,-2),P3(-2,0),P4(0,2),由此可见是四个点一循环.又因为2013÷4=503……1,所以点P2013的坐标与点P1(2,0)一样.
4.【解析】因为点A与点A1关于x轴对称,
所以点A1的坐标为(-3,2),
又因为点A1与点A2关于y轴对称,
所以点A2的坐标为(3,2).
答案:(3,2)
5.【解析】根据A与A′,B与B′的坐标关系知,△ABC与△A′B′C′关于x轴对称,故点C的坐标为(-5,0).
答案:(-5,0)
6.【解析】根据题意,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,经过观察图形,动手操作不难发现,每3次为一个周期变换.依次类推第2013次变换相当于2013=671×3次变换,也就是说第2013次变换时已经有671次重复,相当于开始的图形,此时A点的坐标是(a,b).
答案:(a,b)
7.【解析】(1)由A,C两点的坐标就可以确定直角坐标系;
(2)根据轴对称的作图方法,便可作出△ABC关于y轴对称的△A′B′C′;
(3)因为点B的坐标为(-2,1),所以它关于y轴对称的点B′的坐标为(2,1).
8.【解析】(1)△A′OB′各顶点的坐标分别为O(0,0),A′(-2,-3),B′(2,-3).
(2)△OA″B″各顶点的坐标为O(0,0),A″(-4,-6),B″(4,-6),由图可得A′B′=4,OC=3,A″B″=8,OD=6,所以S△A′B′O=×4×3=6.
S△A″B″O=×8×6=24.所以,将△A′B′O各顶点坐标都分别乘2后的三角形面积是△A′B′O的面积的4倍.
PAGE
-
1
-
