七年级上2.3简单的轴对称图形(2)同步测试含答案解析
文档属性
| 名称 | 七年级上2.3简单的轴对称图形(2)同步测试含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 130.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 00:00:00 | ||
图片预览



文档简介
知能提升作业(十三)
第2课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
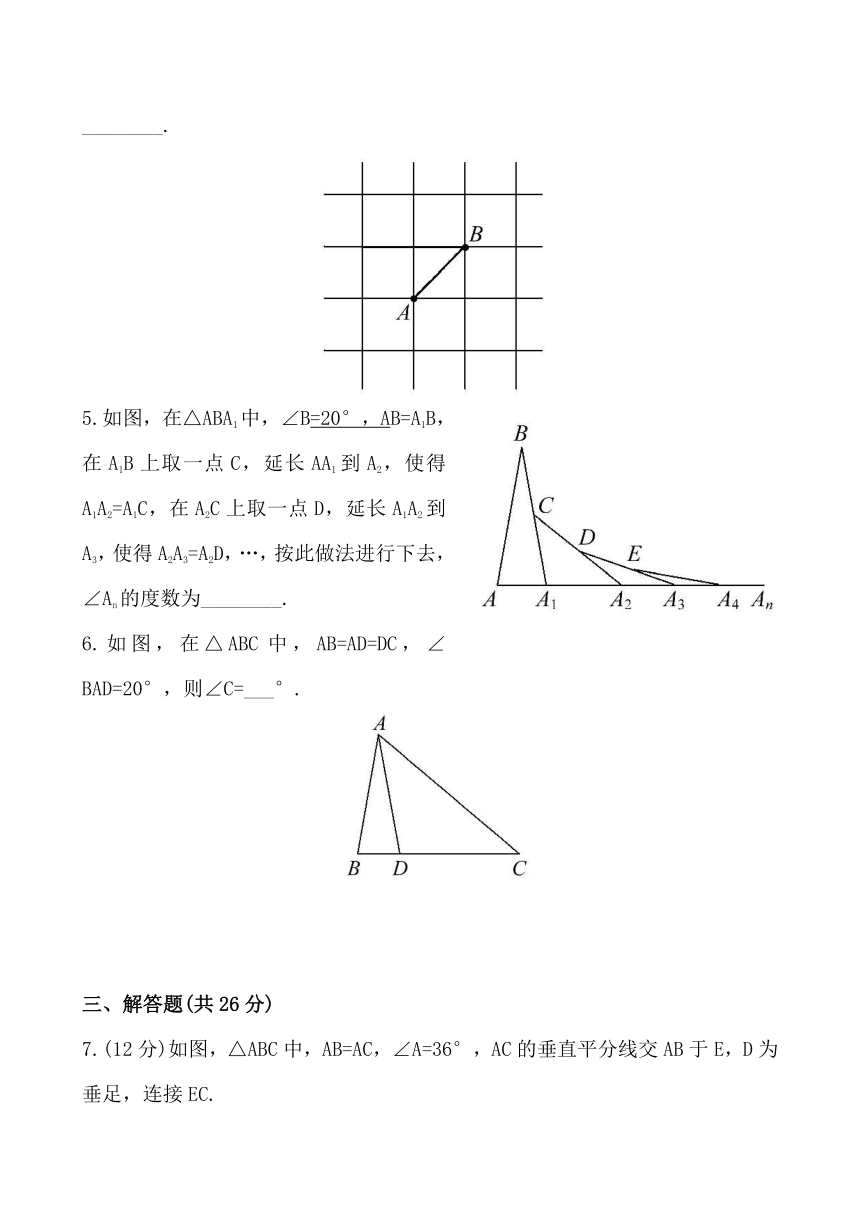
1.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,DE⊥BC,DF⊥AC,垂足分别为D,E,F,则图中的线段存在2倍关系的有( )
(A)7组
(B)8组
(C)9组
(D)10组
2.如图所示,AOB是一钢架,且∠AOB
( http: / / www.21cnjy.com )=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE相等,则最多能添加这样的钢管的条数为( )
( http: / / www.21cnjy.com )
(A)7
(B)8
(C)9
(D)10
3.如图,在△ABC中,AD是△ABC的角平分线,AC=AB+BD,下列正确的是( )
( http: / / www.21cnjy.com )
(A)∠B=∠C
(B)∠B=2∠C
(C)∠B=3∠C
(D)∠B=∠C
二、填空题(每小题4分,共12分)
4.如图所示的正方形网格中,网格线的交点称
( http: / / www.21cnjy.com )为格点,已知A,B两格点,如果点C也是图中的格点,且使得△ABC为等腰三角形,则满足条件的点C的个数是________.
( http: / / www.21cnjy.com )
5.如图,在△ABA1中,∠B=20°,A
( http: / / www.21cnjy.com )B=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,…,按此做法进行下去,∠An的度数为________.
6.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C=___°.
( http: / / www.21cnjy.com )
三、解答题(共26分)
7.(12分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数.
(2)若EC=5,求BC长.
( http: / / www.21cnjy.com )
【拓展延伸】
8.(14分)如图,已知等
( http: / / www.21cnjy.com )边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必说明理由.
(2)如图②,当点M在BC上时,其他条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②给出推理过程;若不成立,请说明理由.
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必说明理由.
( http: / / www.21cnjy.com )
答案解析
1.【解析】选B.根据题意可知,图中所
( http: / / www.21cnjy.com )有的直角三角形都含有30°角,所以每个三角形中都有一组线段满足2倍关系,共有7个三角形,同时由于CE与DF相等,所以共有8组.
2.【解析】选B.因为添加的钢管长
( http: / / www.21cnjy.com )度都与OE相等,∠AOB=10°,所以∠GEF=∠FGE=20°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是10°,第二个是20°,第三个是30°,第四个是40°,第五个是
50°,第六个是60°,第七个是70°,第八个是80°,第九个是90°就不存在了.所以一共有8个.
3.【解析】选B.在AC上取点E,使得AE=AB,连接DE.
因为AD平分∠BAC,
所以∠BAD=∠EAD.
因为AD=AD,AB=AE.
所以△ABD≌△AED(SAS).
所以BD=DE,∠B=∠AED.
又因为AC=AB+BD,
所以EC=BD=DE.
所以△EDC是等腰三角形,所以∠C=∠EDC.
所以∠AED=∠C+∠EDC=2∠C.
所以∠B=2∠C.
4.【解析】如图,以AB为底边的点有4个,在线段AB的垂直平分线上,以AB为腰的有4个.
( http: / / www.21cnjy.com )
答案:8
5.【解析】在△ABA1中,因为∠B=20°,AB=A1B,
所以∠AA1B=80°.
在△A1A2C中,因为A1A2=A1C,
所以∠A1A2C=∠AA1B=×80°
=()2-1×80°=40°.
在△A2A3D中,
因为A2A3=A2D,
所以∠A2A3D=∠A1A2C=××80°
=()3-1×80°=20°,
依此类推,得∠An的度数为()n-1·80°.
答案:()n-1·80°(或)
6.【解析】因为AB=AD=DC,所以∠ABD=∠ADB,∠C=∠DAC,
由三角形的内角和定理得:∠ADB==80°,
所以∠C=×80°=40°.
答案:40
7.【解析】(1)方法一:因为DE垂直平分AC,
所以CE=AE,
所以∠ECD=∠A=36°.
方法二:因为DE垂直平分AC,
所以AD=CD,∠ADE=∠CDE=90°.
又因为DE
=DE,所以△ADE≌△CDE,
所以∠ECD=∠A=36°.
(2)方法一:因为AB=AC,∠A=36°,
所以∠B=∠ACB=72°.
因为∠ECD=36°,
所以∠BCE=∠ACB-∠ECD=36°,
所以∠BEC=72°=∠B,
所以BC=EC=5.
方法二:因为AB=AC,∠A=36°,
所以∠B=∠ACB=72°,
所以∠BEC=∠A+∠ECD=72°,
所以∠BEC=∠B,
所以BC=EC=5.
【归纳整合】
构造等腰三角形的“四个方法”
在等腰三角形的性质与判定的综合运用中,常见的构造等腰三角形的模式有:
(1)“角平分线+平行线”构造等腰三角形,应用平行线的性质得到角的相等关系,应用等角对等边得到边的相等.
(2)“角平分线+垂线”构造等腰三角形,应用的原理是逆用等腰三角形的三线合一性质定理.
(3)应用“垂直平分线”构造等腰三角形.
(4)用“三角形中角的2倍关系”构造等腰三角形.
8.【解析】(1)判断:EN与MF相等(或EN=MF),点F在直线NE上.
(2)成立.
理由:延长EN,则EN过点F.
因为△ABC是等边三角形,
所以AB=AC=BC.
又因为D,E,F是三边的中点,连接DF,
所以EF=DF=BF.
因为∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
所以∠BDM=∠FDN.
又因为DM=DN,∠ABM=∠DFN=60°,
所以△DBM≌△DFN.
所以BM=FN.
因为BF=EF,
所以MF=EN.
( http: / / www.21cnjy.com )
(3)画出图形(连出线段EN),
MF与EN相等的结论仍然成立(或MF=EN成立).
( http: / / www.21cnjy.com )
第2课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,DE⊥BC,DF⊥AC,垂足分别为D,E,F,则图中的线段存在2倍关系的有( )
(A)7组
(B)8组
(C)9组
(D)10组
2.如图所示,AOB是一钢架,且∠AOB
( http: / / www.21cnjy.com )=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与OE相等,则最多能添加这样的钢管的条数为( )
( http: / / www.21cnjy.com )
(A)7
(B)8
(C)9
(D)10
3.如图,在△ABC中,AD是△ABC的角平分线,AC=AB+BD,下列正确的是( )
( http: / / www.21cnjy.com )
(A)∠B=∠C
(B)∠B=2∠C
(C)∠B=3∠C
(D)∠B=∠C
二、填空题(每小题4分,共12分)
4.如图所示的正方形网格中,网格线的交点称
( http: / / www.21cnjy.com )为格点,已知A,B两格点,如果点C也是图中的格点,且使得△ABC为等腰三角形,则满足条件的点C的个数是________.
( http: / / www.21cnjy.com )
5.如图,在△ABA1中,∠B=20°,A
( http: / / www.21cnjy.com )B=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,…,按此做法进行下去,∠An的度数为________.
6.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C=___°.
( http: / / www.21cnjy.com )
三、解答题(共26分)
7.(12分)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数.
(2)若EC=5,求BC长.
( http: / / www.21cnjy.com )
【拓展延伸】
8.(14分)如图,已知等
( http: / / www.21cnjy.com )边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必说明理由.
(2)如图②,当点M在BC上时,其他条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②给出推理过程;若不成立,请说明理由.
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必说明理由.
( http: / / www.21cnjy.com )
答案解析
1.【解析】选B.根据题意可知,图中所
( http: / / www.21cnjy.com )有的直角三角形都含有30°角,所以每个三角形中都有一组线段满足2倍关系,共有7个三角形,同时由于CE与DF相等,所以共有8组.
2.【解析】选B.因为添加的钢管长
( http: / / www.21cnjy.com )度都与OE相等,∠AOB=10°,所以∠GEF=∠FGE=20°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是10°,第二个是20°,第三个是30°,第四个是40°,第五个是
50°,第六个是60°,第七个是70°,第八个是80°,第九个是90°就不存在了.所以一共有8个.
3.【解析】选B.在AC上取点E,使得AE=AB,连接DE.
因为AD平分∠BAC,
所以∠BAD=∠EAD.
因为AD=AD,AB=AE.
所以△ABD≌△AED(SAS).
所以BD=DE,∠B=∠AED.
又因为AC=AB+BD,
所以EC=BD=DE.
所以△EDC是等腰三角形,所以∠C=∠EDC.
所以∠AED=∠C+∠EDC=2∠C.
所以∠B=2∠C.
4.【解析】如图,以AB为底边的点有4个,在线段AB的垂直平分线上,以AB为腰的有4个.
( http: / / www.21cnjy.com )
答案:8
5.【解析】在△ABA1中,因为∠B=20°,AB=A1B,
所以∠AA1B=80°.
在△A1A2C中,因为A1A2=A1C,
所以∠A1A2C=∠AA1B=×80°
=()2-1×80°=40°.
在△A2A3D中,
因为A2A3=A2D,
所以∠A2A3D=∠A1A2C=××80°
=()3-1×80°=20°,
依此类推,得∠An的度数为()n-1·80°.
答案:()n-1·80°(或)
6.【解析】因为AB=AD=DC,所以∠ABD=∠ADB,∠C=∠DAC,
由三角形的内角和定理得:∠ADB==80°,
所以∠C=×80°=40°.
答案:40
7.【解析】(1)方法一:因为DE垂直平分AC,
所以CE=AE,
所以∠ECD=∠A=36°.
方法二:因为DE垂直平分AC,
所以AD=CD,∠ADE=∠CDE=90°.
又因为DE
=DE,所以△ADE≌△CDE,
所以∠ECD=∠A=36°.
(2)方法一:因为AB=AC,∠A=36°,
所以∠B=∠ACB=72°.
因为∠ECD=36°,
所以∠BCE=∠ACB-∠ECD=36°,
所以∠BEC=72°=∠B,
所以BC=EC=5.
方法二:因为AB=AC,∠A=36°,
所以∠B=∠ACB=72°,
所以∠BEC=∠A+∠ECD=72°,
所以∠BEC=∠B,
所以BC=EC=5.
【归纳整合】
构造等腰三角形的“四个方法”
在等腰三角形的性质与判定的综合运用中,常见的构造等腰三角形的模式有:
(1)“角平分线+平行线”构造等腰三角形,应用平行线的性质得到角的相等关系,应用等角对等边得到边的相等.
(2)“角平分线+垂线”构造等腰三角形,应用的原理是逆用等腰三角形的三线合一性质定理.
(3)应用“垂直平分线”构造等腰三角形.
(4)用“三角形中角的2倍关系”构造等腰三角形.
8.【解析】(1)判断:EN与MF相等(或EN=MF),点F在直线NE上.
(2)成立.
理由:延长EN,则EN过点F.
因为△ABC是等边三角形,
所以AB=AC=BC.
又因为D,E,F是三边的中点,连接DF,
所以EF=DF=BF.
因为∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
所以∠BDM=∠FDN.
又因为DM=DN,∠ABM=∠DFN=60°,
所以△DBM≌△DFN.
所以BM=FN.
因为BF=EF,
所以MF=EN.
( http: / / www.21cnjy.com )
(3)画出图形(连出线段EN),
MF与EN相等的结论仍然成立(或MF=EN成立).
( http: / / www.21cnjy.com )
