七年级上2.3简单的轴对称图形(1)同步测试含答案解析
文档属性
| 名称 | 七年级上2.3简单的轴对称图形(1)同步测试含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 00:00:00 | ||
图片预览

文档简介
知能提升作业(十二)
3 简单的轴对称图形
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图所示,已知EF垂直平分AD交BC的延长线于F,连接AF,且AB=AF,则AB与DF的关系是( )
(A)AB>DF
(B)AB(C)AB=DF
(D)不能确定
2.如图,△ABC的周长为21,并且AB=AC,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
(A)13
(B)14
(C)15
(D)16
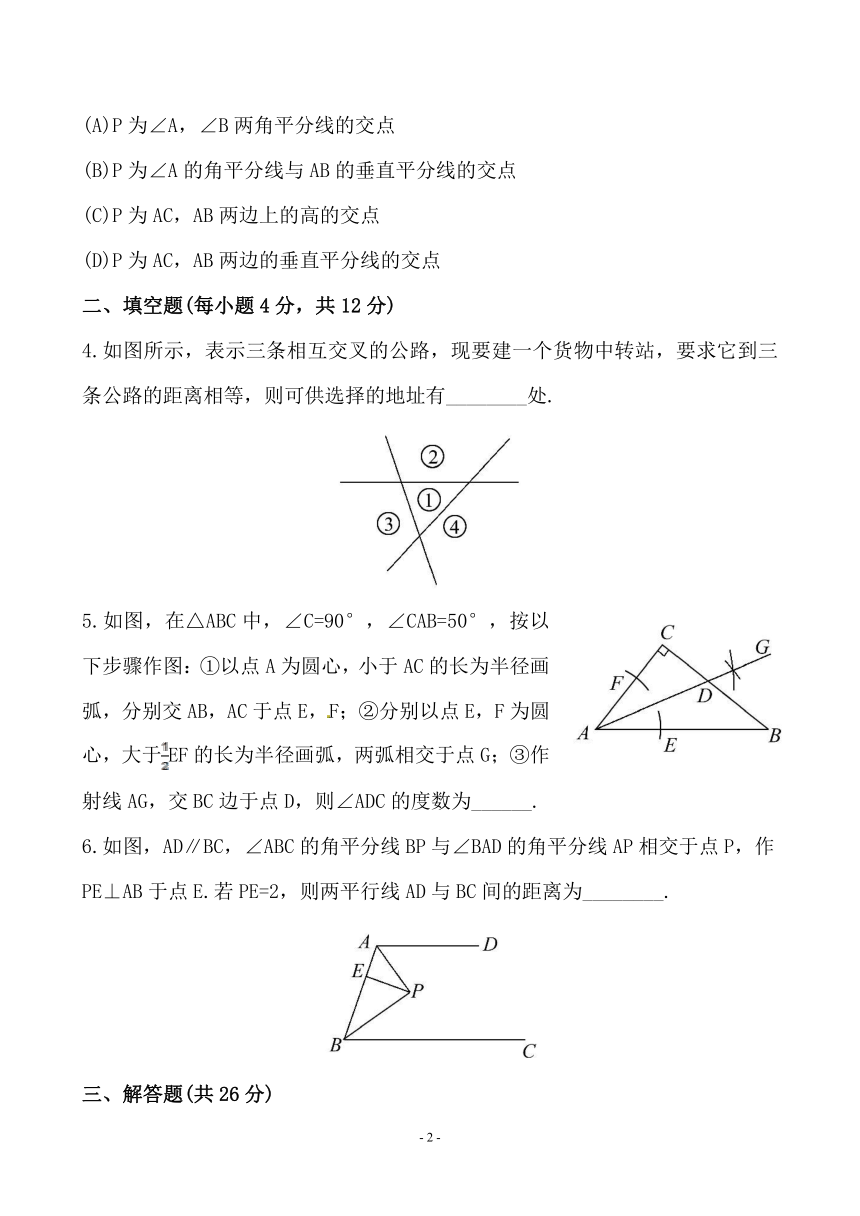
3.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( )
(A)P为∠A,∠B两角平分线的交点
(B)P为∠A的角平分线与AB的垂直平分线的交点
(C)P为AC,AB两边上的高的交点
(D)P为AC,AB两边的垂直平分线的交点
二、填空题(每小题4分,共12分)
4.如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有________处.
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为______.
6.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为________.
三、解答题(共26分)
7.
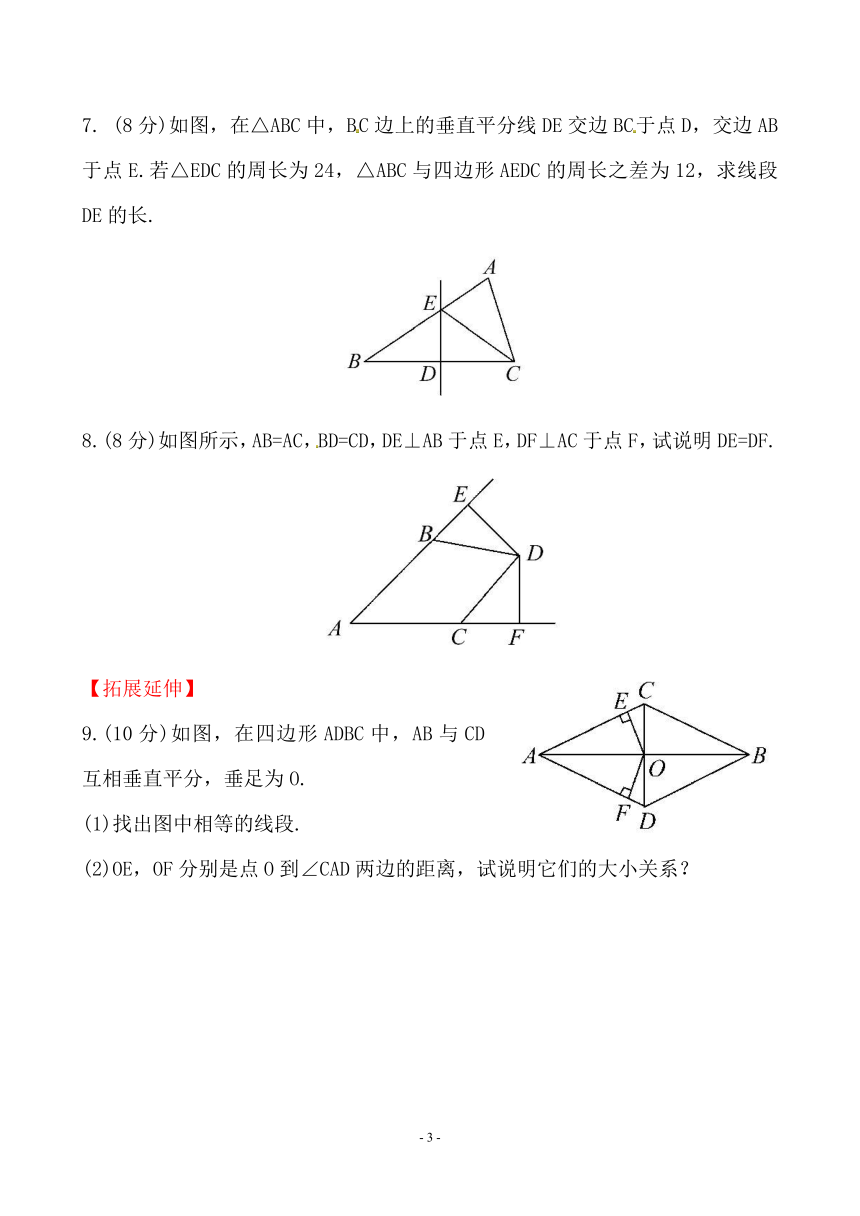
(8分)如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长.
8.(8分)如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试说明DE=DF.
【拓展延伸】
9.(10分)如图,在四边形ADBC中,AB与CD互相垂直平分,垂足为O.
(1)找出图中相等的线段.
(2)OE,OF分别是点O到∠CAD两边的距离,试说明它们的大小关系?
答案解析
1.【解析】选C.因为EF垂直平分AD,
所以AF=DF.
因为AB=AF,所以AB=DF.
2.【解析】选A.由△ABC的周长为21.AB=AC,BC=5.得AB=AC==8,
又由DE为AB的垂直平分线,所以BE=AE,
△BEC的周长为BE+EC+BC=AE+EC+BC=AC+BC=8+5=13.
【归纳整合】线段垂直平分线的性质是说明线段、角相等的重要方法.一般情况下,利用线段垂直平分线的性质,把已知线段转换成与求证关系密切的线段,从而解决计算求值和证明的问题.
3.【解析】选B.要使点P到∠A的两边的距离相等,则点P应在∠A的角平分线上;要使PA=PB,点P应在AB的垂直平分线上,所以点P为∠A的角平分线与AB的垂直平分线的交点.
4.【解析】如图,点A,B,C为外角平分线的交点,O为内角平分线交点,这四个点均符合要求.
答案:4
5.【解析】根据作图可知AG平分∠CAB,由直角三角形两锐角互余,所以∠ADC=
90°-25°=65°.
答案:65°
6.【解析】过P点作PM⊥AD于M,PN⊥BC于N,
则M,N,P三点共线,
因为BP平分∠ABC,AP平分∠BAD,
PE⊥AB于点E,PM⊥AD于M,PN⊥BC于N.
所以PN=PE=PM(角平分线上的点到角两边的距离相等).
因为PE=2,所以PM=PN=2.所以MN=4.
答案:4
7.【解析】因为DE是BC边上的垂直平分线,
所以BE=CE,BD=DC.
因为△EDC的周长为24,
△ABC与四边形AEDC的周长之差为12,
所以ED+DC+EC=24,①
BE+BD-DE=12.②
①-②得,DE=6.
8.【解析】连接AD,
在△ABD和△ACD中,
所以△ABD≌△ACD(SSS),
所以∠BAD=∠CAD,
即AD平分∠BAC.
又因为DE⊥AB于点E,DF⊥AC于点F,
所以DE=DF(角平分线上的点到角两边的距离相等).
9.【解析】(1)AC=BC=AD=BD,
OC=OD,OA=OB,AE=AF,EC=FD,OE=OF.
(2)OE=OF.
方法一:因为AB垂直平分CD,
所以∠AOC=∠AOD,CO=OD,
在△AOC和△AOD中,
,
所以△AOC≌△AOD(SAS),
所以∠CAO=∠DAO,
又因为OE⊥AC,OF⊥AD,
所以OE=OF.
方法二:因为CO=DO,AO⊥CD.
所以S△AOC=AO·OC=DO·AO=S△AOD,
又因为S△AOC=AC·OE,
S△AOD=AD·OF,
因为AC=AD,
所以OE=OF.
PAGE
-
1
-
3 简单的轴对称图形
第1课时
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图所示,已知EF垂直平分AD交BC的延长线于F,连接AF,且AB=AF,则AB与DF的关系是( )
(A)AB>DF
(B)AB
(D)不能确定
2.如图,△ABC的周长为21,并且AB=AC,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
(A)13
(B)14
(C)15
(D)16
3.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( )
(A)P为∠A,∠B两角平分线的交点
(B)P为∠A的角平分线与AB的垂直平分线的交点
(C)P为AC,AB两边上的高的交点
(D)P为AC,AB两边的垂直平分线的交点
二、填空题(每小题4分,共12分)
4.如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有________处.
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为______.
6.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为________.
三、解答题(共26分)
7.
(8分)如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,求线段DE的长.
8.(8分)如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试说明DE=DF.
【拓展延伸】
9.(10分)如图,在四边形ADBC中,AB与CD互相垂直平分,垂足为O.
(1)找出图中相等的线段.
(2)OE,OF分别是点O到∠CAD两边的距离,试说明它们的大小关系?
答案解析
1.【解析】选C.因为EF垂直平分AD,
所以AF=DF.
因为AB=AF,所以AB=DF.
2.【解析】选A.由△ABC的周长为21.AB=AC,BC=5.得AB=AC==8,
又由DE为AB的垂直平分线,所以BE=AE,
△BEC的周长为BE+EC+BC=AE+EC+BC=AC+BC=8+5=13.
【归纳整合】线段垂直平分线的性质是说明线段、角相等的重要方法.一般情况下,利用线段垂直平分线的性质,把已知线段转换成与求证关系密切的线段,从而解决计算求值和证明的问题.
3.【解析】选B.要使点P到∠A的两边的距离相等,则点P应在∠A的角平分线上;要使PA=PB,点P应在AB的垂直平分线上,所以点P为∠A的角平分线与AB的垂直平分线的交点.
4.【解析】如图,点A,B,C为外角平分线的交点,O为内角平分线交点,这四个点均符合要求.
答案:4
5.【解析】根据作图可知AG平分∠CAB,由直角三角形两锐角互余,所以∠ADC=
90°-25°=65°.
答案:65°
6.【解析】过P点作PM⊥AD于M,PN⊥BC于N,
则M,N,P三点共线,
因为BP平分∠ABC,AP平分∠BAD,
PE⊥AB于点E,PM⊥AD于M,PN⊥BC于N.
所以PN=PE=PM(角平分线上的点到角两边的距离相等).
因为PE=2,所以PM=PN=2.所以MN=4.
答案:4
7.【解析】因为DE是BC边上的垂直平分线,
所以BE=CE,BD=DC.
因为△EDC的周长为24,
△ABC与四边形AEDC的周长之差为12,
所以ED+DC+EC=24,①
BE+BD-DE=12.②
①-②得,DE=6.
8.【解析】连接AD,
在△ABD和△ACD中,
所以△ABD≌△ACD(SSS),
所以∠BAD=∠CAD,
即AD平分∠BAC.
又因为DE⊥AB于点E,DF⊥AC于点F,
所以DE=DF(角平分线上的点到角两边的距离相等).
9.【解析】(1)AC=BC=AD=BD,
OC=OD,OA=OB,AE=AF,EC=FD,OE=OF.
(2)OE=OF.
方法一:因为AB垂直平分CD,
所以∠AOC=∠AOD,CO=OD,
在△AOC和△AOD中,
,
所以△AOC≌△AOD(SAS),
所以∠CAO=∠DAO,
又因为OE⊥AC,OF⊥AD,
所以OE=OF.
方法二:因为CO=DO,AO⊥CD.
所以S△AOC=AO·OC=DO·AO=S△AOD,
又因为S△AOC=AC·OE,
S△AOD=AD·OF,
因为AC=AD,
所以OE=OF.
PAGE
-
1
-
