七年级上2.2探索轴对称的性质同步测试含答案解析
文档属性
| 名称 | 七年级上2.2探索轴对称的性质同步测试含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-01 00:00:00 | ||
图片预览

文档简介
知能提升作业(十一)
2 探索轴对称的性质
(30分钟
50分)
一、选择题(每小题4分,共12分)
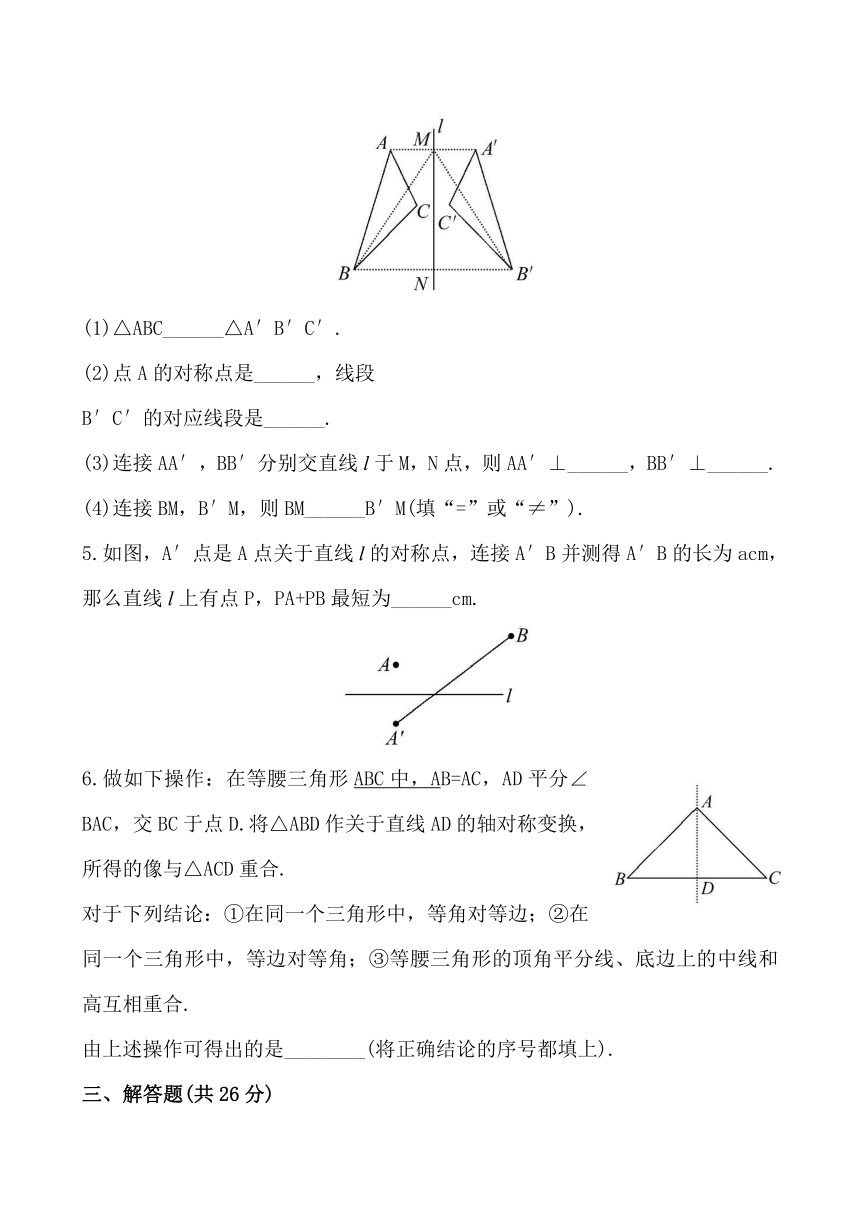
1.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
(A)40°
(B)30°
(C)20°
(D)10°
2.如图,∠AOB内一点P,P1,P2分别是P关于OA,OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
(A)3
cm
(B)4
cm
(C)5
cm
(D)6
cm
3.将一个矩形纸片依次按图(1)、图
(2)的方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所得到的图案是( )
( http: / / www.21cnjy.com )
二、填空题(每小题4分,共12分)
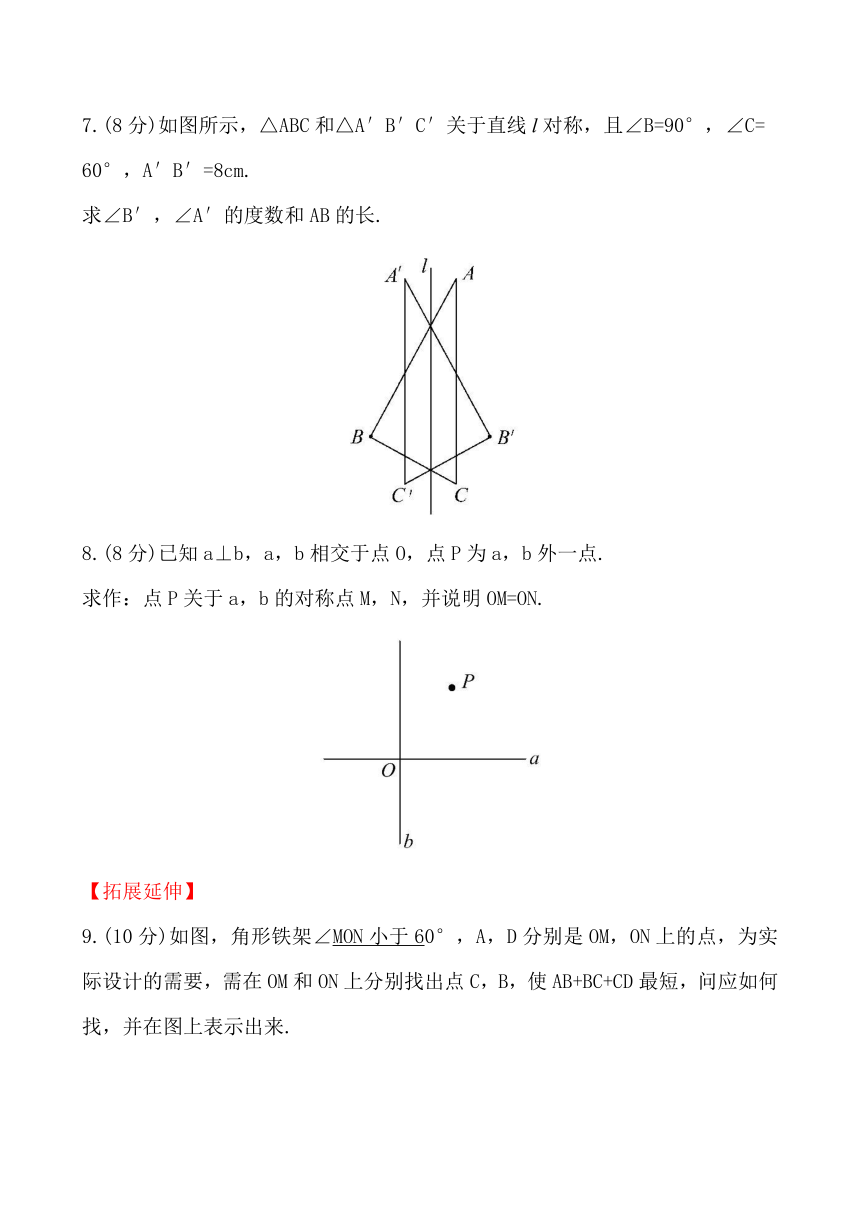
4.如图,△ABC与△A′B′C′关于直线l对称,回答下列问题:
( http: / / www.21cnjy.com )
(1)△ABC______△A′B′C′.
(2)点A的对称点是______,线段
B′C′的对应线段是______.
(3)连接AA′,BB′分别交直线l于M,N点,则AA′⊥______,BB′⊥______.
(4)连接BM,B′M,则BM______B′M(填“=”或“≠”).
5.如图,A′点是A点关于直线l的对称点,连接A′B并测得A′B的长为acm,那么直线l上有点P,PA+PB最短为______cm.
( http: / / www.21cnjy.com )
6.做如下操作:在等腰三角形ABC中,A
( http: / / www.21cnjy.com )B=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是________(将正确结论的序号都填上).
三、解答题(共26分)
7.(8分)如图所示,△ABC和△A′B′C′关于直线l对称,且∠B=90°,∠C=
60°,A′B′=8cm.
求∠B′,∠A′的度数和AB的长.
( http: / / www.21cnjy.com )
8.(8分)已知a⊥b,a,b相交于点O,点P为a,b外一点.
求作:点P关于a,b的对称点M,N,并说明OM=ON.
( http: / / www.21cnjy.com )
【拓展延伸】
9.(10分)如图,角形铁架∠MON小于6
( http: / / www.21cnjy.com )0°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
( http: / / www.21cnjy.com )
答案解析
1.【解析】选D.△ADC与△A′DC关于CD成轴对称,∠A=∠CA′D=50°,∠ACB=
90°,∠B=40°,则∠A′DB=50°-
40°=10°.
2.【解析】选C.因为点P1是点P关于OA的对称点,所以OA垂直平分PP1,则P1M
=PM,同理P2N=PN,所以△PMN的周长PM+MN+NP=P1M+MN+NP2=P1P2=5cm.
3.【解析】选A.由图案的对称性进行想象,或动手操作一下都可.
【归纳整合】关于图形折叠实质上就是轴对称的
( http: / / www.21cnjy.com )一种变形应用,解题时,(1)应抓住折叠前后的图形全等.(2)应注意折叠前后的对应关系.画出折叠前后的对比图,找出对应关系.
4.答案:(1)≌ (2)A′ BC (3)MN MN (4)=
5.【解析】P点是A′B与l的交点时,PA+PB最短,此时PA+PB=PA′+PB=a(cm).
答案:a
6.【解析】题意中没有∠B
( http: / / www.21cnjy.com )=∠C这条件,因而不能得出结论①;根据轴对称的性质可以得出∠B=∠C,从而得出结论②;根据等腰三角形的性质“三线合一”可以得出结论③.
答案:②③
7.【解析】因为△ABC和△A′B′C′关于直线l对称,所以△ABC≌
△A′B′C′,
所以∠B′=∠B,∠C′=∠C,A′B′=AB=8cm,所以∠B′=90°,∠C′=60°,
所以∠A′=180°-90°-60°=30°.
答:∠B′,∠A′分别是90°和30°,AB的长为8cm.
8.【解析】作法:(1)过点P作PC⊥a,
并延长PC到M,使CM=PC.
(2)过点P作PD⊥b,并延长PD到N,使得DN=PD.
( http: / / www.21cnjy.com )
则点M,N就是点P关于a,b的对称点.
理由:连接ON,OP,OM.
因为点P与点M关于直线a对称,
所以直线a是线段PM的中垂线.
所以OP=OM.
同理可得OP=ON.
所以OM=ON.
9.【解析】如图,作点A关于ON的对称
( http: / / www.21cnjy.com )点A1,点D关于OM的对称点D1,连接A1D1,分别交OM,ON于点C,B,则点B,C就是所求的点.
( http: / / www.21cnjy.com )
2 探索轴对称的性质
(30分钟
50分)
一、选择题(每小题4分,共12分)
1.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
(A)40°
(B)30°
(C)20°
(D)10°
2.如图,∠AOB内一点P,P1,P2分别是P关于OA,OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是( )
(A)3
cm
(B)4
cm
(C)5
cm
(D)6
cm
3.将一个矩形纸片依次按图(1)、图
(2)的方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所得到的图案是( )
( http: / / www.21cnjy.com )
二、填空题(每小题4分,共12分)
4.如图,△ABC与△A′B′C′关于直线l对称,回答下列问题:
( http: / / www.21cnjy.com )
(1)△ABC______△A′B′C′.
(2)点A的对称点是______,线段
B′C′的对应线段是______.
(3)连接AA′,BB′分别交直线l于M,N点,则AA′⊥______,BB′⊥______.
(4)连接BM,B′M,则BM______B′M(填“=”或“≠”).
5.如图,A′点是A点关于直线l的对称点,连接A′B并测得A′B的长为acm,那么直线l上有点P,PA+PB最短为______cm.
( http: / / www.21cnjy.com )
6.做如下操作:在等腰三角形ABC中,A
( http: / / www.21cnjy.com )B=AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的像与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是________(将正确结论的序号都填上).
三、解答题(共26分)
7.(8分)如图所示,△ABC和△A′B′C′关于直线l对称,且∠B=90°,∠C=
60°,A′B′=8cm.
求∠B′,∠A′的度数和AB的长.
( http: / / www.21cnjy.com )
8.(8分)已知a⊥b,a,b相交于点O,点P为a,b外一点.
求作:点P关于a,b的对称点M,N,并说明OM=ON.
( http: / / www.21cnjy.com )
【拓展延伸】
9.(10分)如图,角形铁架∠MON小于6
( http: / / www.21cnjy.com )0°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
( http: / / www.21cnjy.com )
答案解析
1.【解析】选D.△ADC与△A′DC关于CD成轴对称,∠A=∠CA′D=50°,∠ACB=
90°,∠B=40°,则∠A′DB=50°-
40°=10°.
2.【解析】选C.因为点P1是点P关于OA的对称点,所以OA垂直平分PP1,则P1M
=PM,同理P2N=PN,所以△PMN的周长PM+MN+NP=P1M+MN+NP2=P1P2=5cm.
3.【解析】选A.由图案的对称性进行想象,或动手操作一下都可.
【归纳整合】关于图形折叠实质上就是轴对称的
( http: / / www.21cnjy.com )一种变形应用,解题时,(1)应抓住折叠前后的图形全等.(2)应注意折叠前后的对应关系.画出折叠前后的对比图,找出对应关系.
4.答案:(1)≌ (2)A′ BC (3)MN MN (4)=
5.【解析】P点是A′B与l的交点时,PA+PB最短,此时PA+PB=PA′+PB=a(cm).
答案:a
6.【解析】题意中没有∠B
( http: / / www.21cnjy.com )=∠C这条件,因而不能得出结论①;根据轴对称的性质可以得出∠B=∠C,从而得出结论②;根据等腰三角形的性质“三线合一”可以得出结论③.
答案:②③
7.【解析】因为△ABC和△A′B′C′关于直线l对称,所以△ABC≌
△A′B′C′,
所以∠B′=∠B,∠C′=∠C,A′B′=AB=8cm,所以∠B′=90°,∠C′=60°,
所以∠A′=180°-90°-60°=30°.
答:∠B′,∠A′分别是90°和30°,AB的长为8cm.
8.【解析】作法:(1)过点P作PC⊥a,
并延长PC到M,使CM=PC.
(2)过点P作PD⊥b,并延长PD到N,使得DN=PD.
( http: / / www.21cnjy.com )
则点M,N就是点P关于a,b的对称点.
理由:连接ON,OP,OM.
因为点P与点M关于直线a对称,
所以直线a是线段PM的中垂线.
所以OP=OM.
同理可得OP=ON.
所以OM=ON.
9.【解析】如图,作点A关于ON的对称
( http: / / www.21cnjy.com )点A1,点D关于OM的对称点D1,连接A1D1,分别交OM,ON于点C,B,则点B,C就是所求的点.
( http: / / www.21cnjy.com )
