第二章 立体几何复习课
图片预览



文档简介
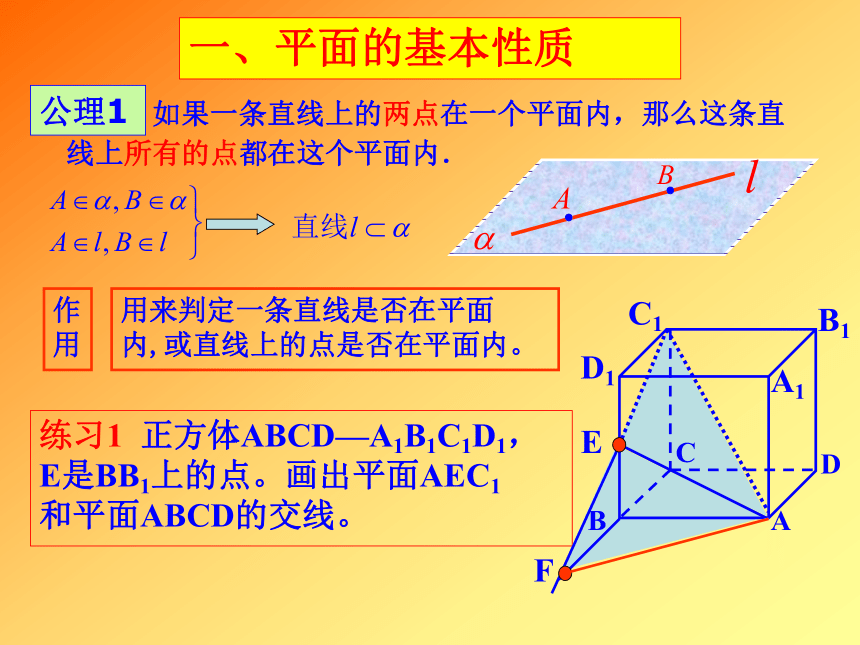
课件50张PPT。高中数学知识点复习第二章立体几何知识结构一.平面的基本性质二.空间两直线的位置关系三.直线和平面平行的判定和性质四.直线和平面垂直的判定和性质五.两个平面平行的判定和性质六.两个平面垂直的判定和性质七.空间向量练习1 正方体ABCD—A1B1C1D1,
E是BB1上的点。画出平面AEC1
和平面ABCD的交线。
一、平面的基本性质 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理1用来判定一条直线是否在平面
内,或直线上的点是否在平面内。
F作用
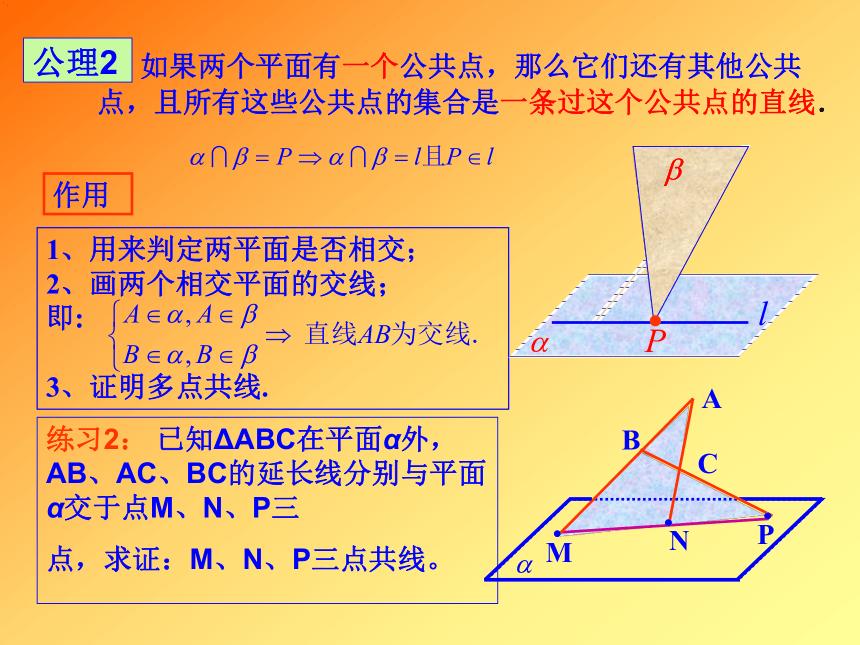
如果两个平面有一个公共点,那么它们还有其他公共
点,且所有这些公共点的集合是一条过这个公共点的直线. 公理21、用来判定两平面是否相交;
2、画两个相交平面的交线;
即:
3、证明多点共线.练习2: 已知ΔABC在平面α外,AB、AC、BC的延长线分别与平面α交于点M、N、P三
点,求证:M、N、P三点共线。
作用
,1、确定平面
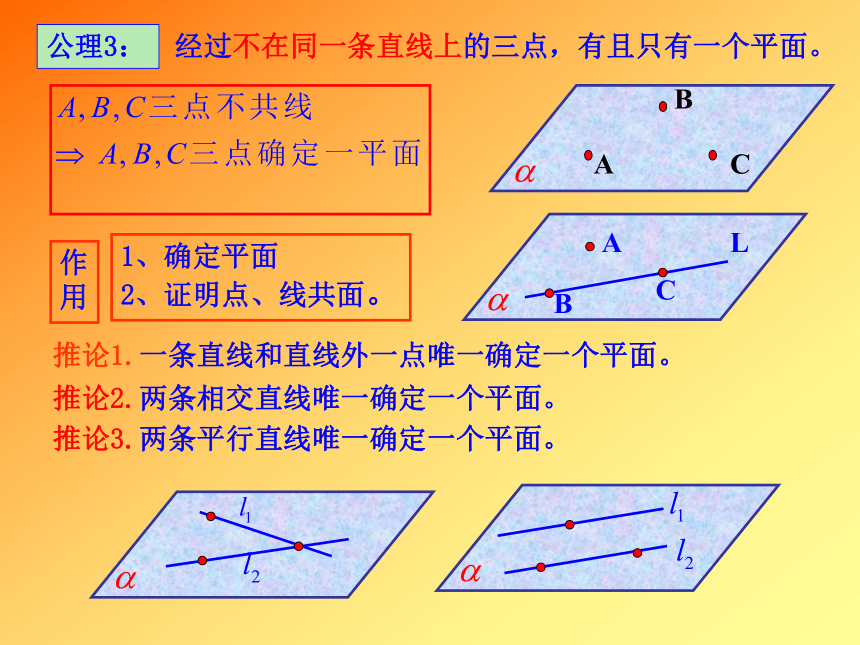
2、证明点、线共面。公理3:经过不在同一条直线上的三点,有且只有一个平面。作用
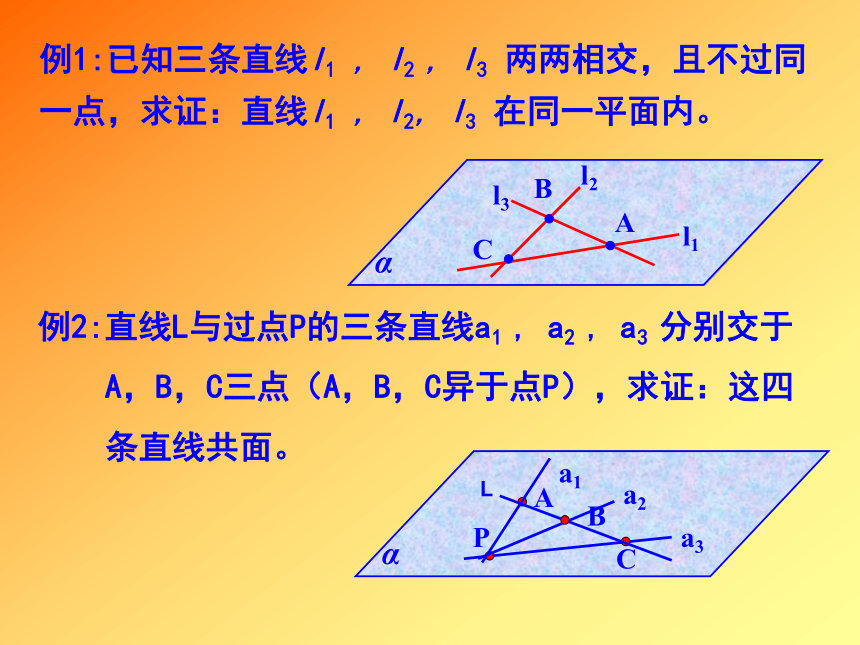
推论1.一条直线和直线外一点唯一确定一个平面。推论2.两条相交直线唯一确定一个平面。推论3.两条平行直线唯一确定一个平面。例1:已知三条直线l1 , l2 , l3 两两相交,且不过同一点,求证:直线l1 , l2, l3 在同一平面内。例2:直线L与过点P的三条直线a1 , a2 , a3 分别交于
A,B,C三点(A,B,C异于点P),求证:这四
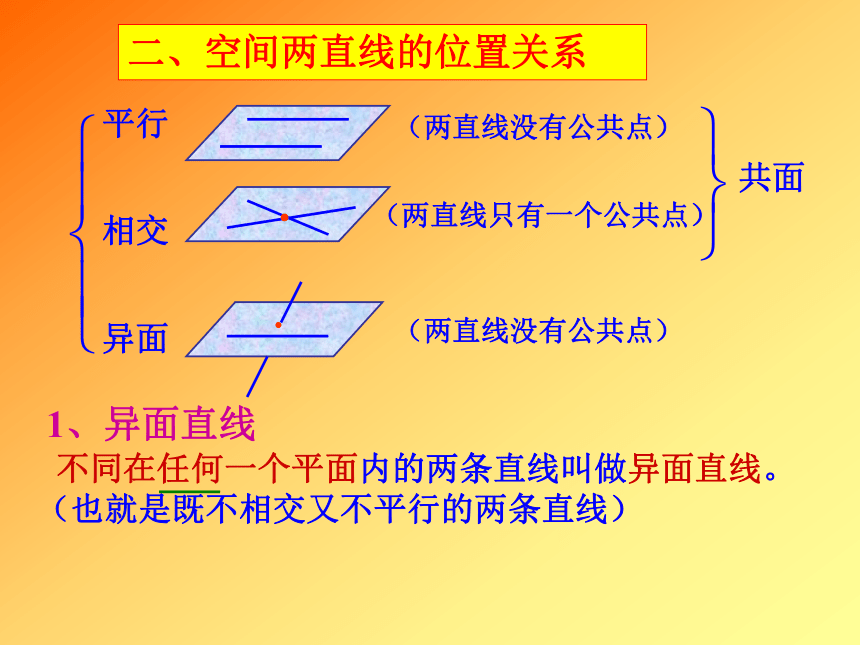
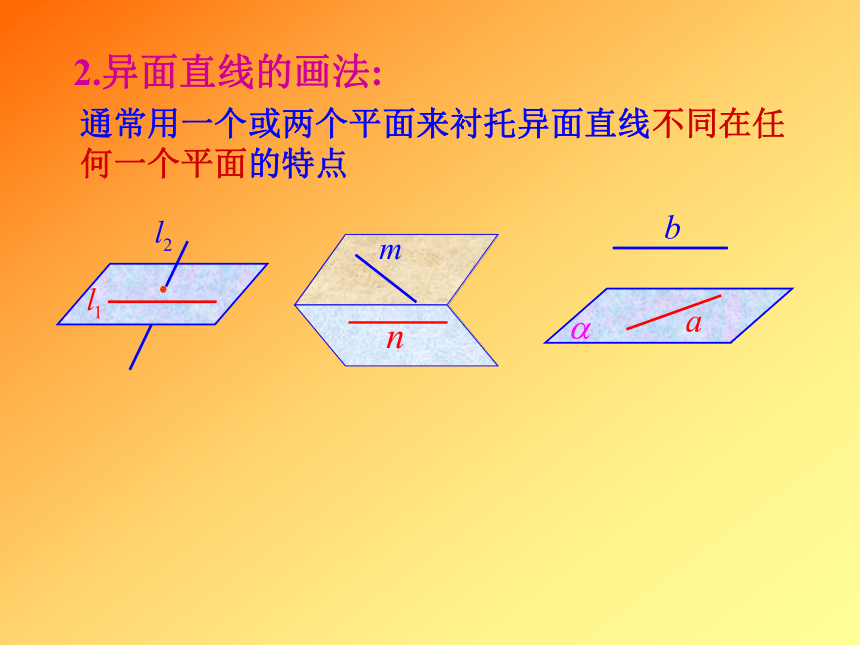
条直线共面。二、空间两直线的位置关系平行相交异面共面(两直线没有公共点)(两直线只有一个公共点)(两直线没有公共点) 不同在任何一个平面内的两条直线叫做异面直线。(也就是既不相交又不平行的两条直线)1、异面直线OEFEFAE和BF是异面直线吗?AE和CF是异面直线吗?2.异面直线的画法:通常用一个或两个平面来衬托异面直线不同在任何一个平面的特点
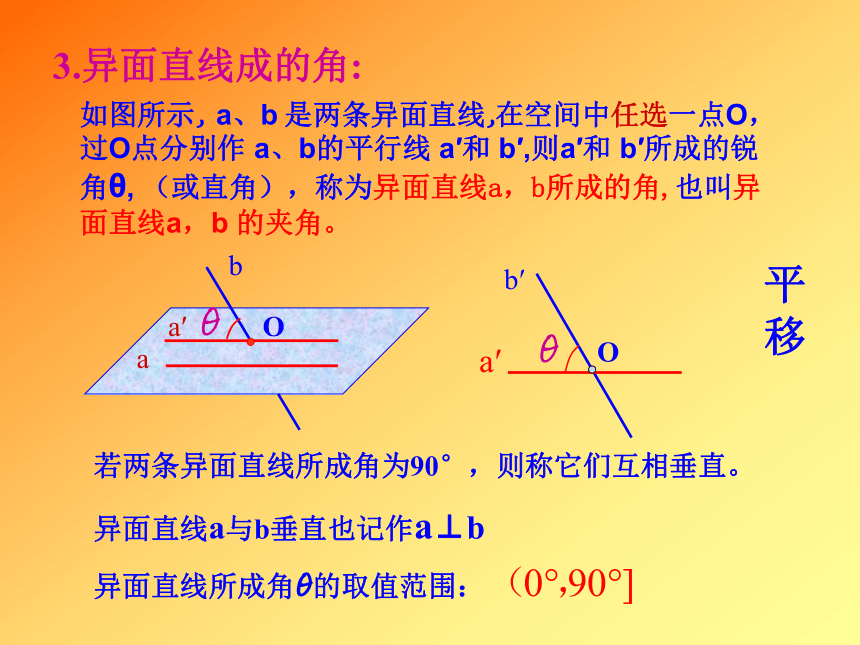
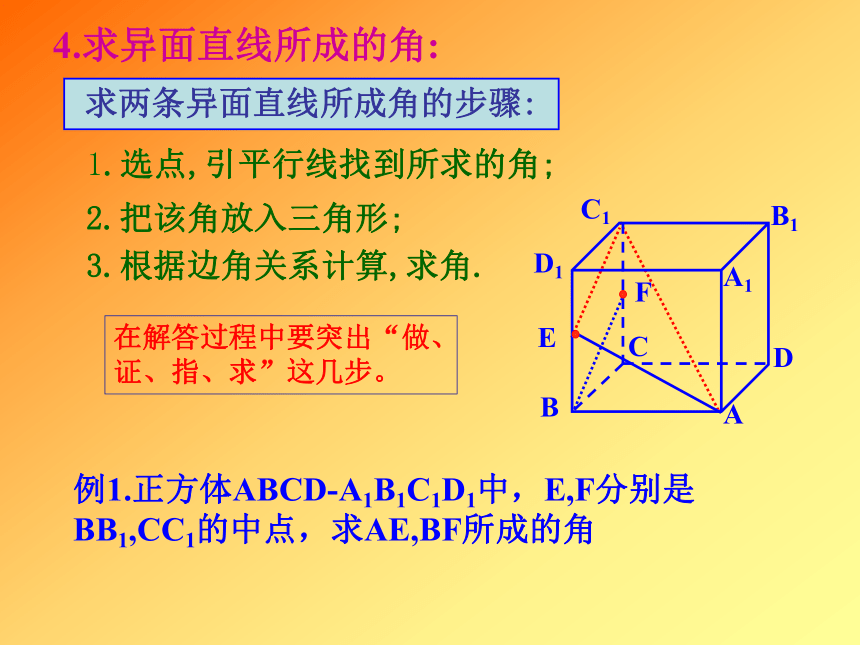
θθ如图所示, a、b 是两条异面直线,在空间中任选一点O,过O点分别作 a、b的平行线 a′和 b′,则a′和 b′所成的锐角θ, (或直角),称为异面直线a,b所成的角,也叫异面直线a,b 的夹角。aba′b′ 若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移3.异面直线成的角:O4.求异面直线所成的角:求两条异面直线所成角的步骤:1.选点,引平行线找到所求的角;2.把该角放入三角形;3.根据边角关系计算,求角.例1.正方体ABCD-A1B1C1D1中,E,F分别是BB1,CC1的中点,求AE,BF所成的角在解答过程中要突出“做、证、指、求”这几步。例2:
已知正方体的棱长为a , M 为 AB 的中点, N为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。解:如图,取A1B1的中点E, 连BE, 有BE∥ A1M 取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角。BG=BE= a, EG = a由余弦定理,cos∠EBG=2/5取EB1的中点F,连NF,有BE∥NF则∠FNC1为所求角。想一想:还有其它定角的方法吗?在△EBG中EG例3.在空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC,AD的中点,求异面直线AM,CN所成角。EG例5.长方体ABCD-A1B1C1D1中,AB=2, BC=1,AA1 =1,求异面直线D1B与AC所成角的余弦值.GAB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?相交直线有几对?平行直线有几对?若a∥b,b∥c,公理4 平行于同一直线的两直线互相平行则a∥c5.平行关系的传递性例1:在正方体ABCD—A1B1C1D1中,直线 AB与C1D1 ,AD1与 BC1 是什么位置关系?为什么?例2 已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。解题思想:把所要解的立体几何问题
转化为平面几何的问题是解立体几何时最主要、最常用的一种方法。6.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。 右图平行六面体中与∠BAD相等的角是哪些角,为什么?
与∠BAD互补的角是哪些,为什么?
填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。平行相交异面平行异面无数无数相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( ) ????判断对错:思考题:
1、a与b是异面直线,且c∥a,则c与b一定( )。
(A)异面 (B)相交 (C)平行 (D)不平行
2、正方体一条对角线与正方体的棱可组成的异面直线的对数
是( )对。
(A)6 (B)3 (C)8 (D)12
3、一条直线和两条异面直线都相交,则它们可以确定( )
平面。
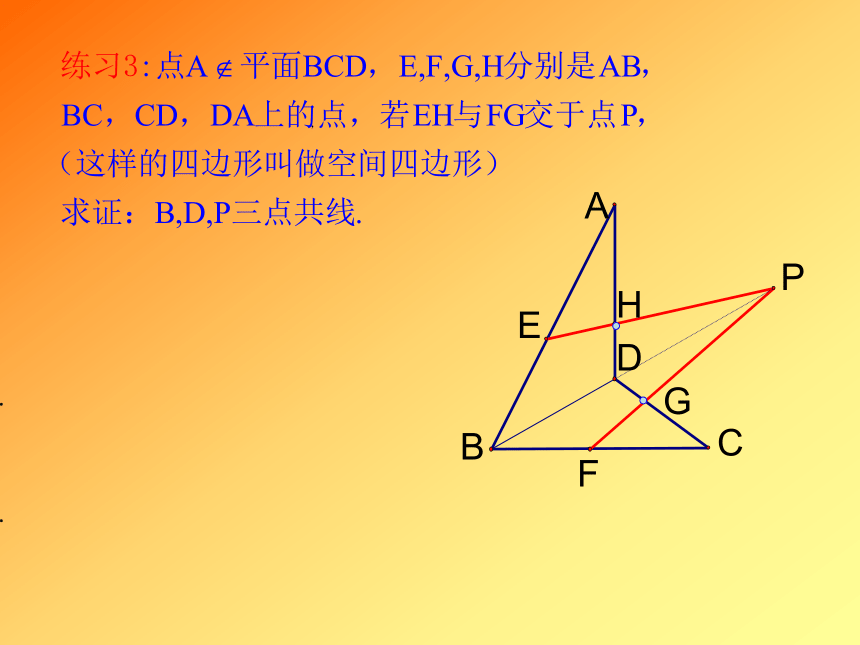
(A)一个 (B)两个 (C)三个 (D)四个三、直线和平面平行的判定和性质定理1.直线和平面的位置关系有哪些?(1)直线在平面内:(2)直线与平面相交:(3)直线与平面平行:2.直线和平面平行的判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)证明直线与平面平行的方法是什么?思考1.在平面内寻找一条直线 2.证明这条直线与已知直线平行.3.直线和平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面与已知平面相交,那么这条直线与交线平行. (线面平行,线线平行)练习:如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个平面垂直。2.直线和平面垂直的判定定理:线不在多,重在相交! 如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。1.直线和平面垂直的定义:四.直线和平面垂直的判定和性质判断对错 ?3.直线和平面垂直的性质定理:性质1如果一条直线垂直于一个平面,那么这条直线垂直于平面的任意一条直线.性质2如果两条平行线中的一条与平面垂直,那么另一条也与这个平面垂直.线线垂直— 线面垂直—线线垂直常用方法例2. 在正方体AC1中,取DD1
的中点E,AC和BD交于O点。 求证:OB1⊥面EAC4.三垂线定理:正射影自一点P向平面 引垂线,垂足Q叫做点P在平面 上的正射影.(简称射影)如果图形F上的所有点在一平面内的射影构成图形F1,则F1叫做图形F在这个平面内的射影.F1O三垂线定理在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直 .三垂线定理的逆定理O在平面内的一条直线,如果它和这个平面的一条斜线垂直, 那么它也和这条斜线的射影垂直 .练习1.如图 为矩形,
由三垂线定理可得到哪些线是垂直的?OEFG2.四面体ABCD中,AB DC
AD BC,求证:AC BDD3.直角三角形ABC中,角C为直角,AC=2,BC= ,PC 平面BCD,PC=3。求点P到直线AB的距离。五.两个平面平行的判定和性质1.空间两个平面的位置关系两个平面平行两个平面相交2. 两个平面平行的判定定理如果一个平面的两条相交直线都与另一个平面平行,那么这两个平面平行。3. 两个平面平行的性质定理1.如果两个平行平面和第三个平面都相交,那么交线互相平行2.如果两个平面平行,那么其中一个平面内的任何一条直线都平行于另一个平面。六.两个平面垂直的判定和性质1. 两个平面垂直的定义(1) 二面角平面内的一条直线把平面分为两部分,其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,每个半平面叫做二面角的面.如图,二面角及表示方法.二面角C-AB- D二面角?-AB- ?二面角(2) 二面角的平面角二面角的大小用它的平面角来度量注意:二面角的平面角必须满足:3)角的边都要垂直于二面角的棱1)角的顶点在棱上2)角的两边分别在两个面内4)二面角的范围是以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角(3) 两个平面垂直的定义:如果两个平面所成的二面角是直二面角,那么就称这两个平面互相垂直.101.利用定义.(4) 二面角的平面角的作法3.作棱的垂面.2.利用三垂线定理及其逆定理.练习:作出下列各图中的二面角的平面角:二面角B—B1C—A OEO二面角A--BC--D二面角C--AD--E四棱锥中取AB 的中点为E,连PE,OE∵O为 AC 中点, ∠ABC=90o∴OE∥BC且 OE BC在Rt△POE中, OE ,PO ∴∴所求的二面角P-AB-C 的正切值为例1.如图,三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O,若PB=AB=1,BC= ,求二面角P-AB-C的正切值。∴∠PEO为二面角P-AB-C 的平面角在Rt△PBE中,BE ,PB=1,PE由三垂线定理知 PE⊥AB解:∴ OE⊥AB ,做证指求答3. 两个平面垂直的性质定理如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面2. 两个平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.七.空间向量.1.空间向量及运算.1.在空间,我们把具有大小和方向的量叫做向量.2.空间向量也用有向线段表示,并且同向且等长的 有向线段表示同一个向量.4.平行于同一个平面的向量叫做共面向量.3.在空间,如果表示向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.5.共线向量定理:对空间任意两个向量 和 , 的充要条件是存在实数 ,使 .6.共面向量定理:如果两个向量
和 不共线, 则向量 与向量
, 共面的充要条件是存在实数
,使 .8. 空间向量基本定理:9.空间向量的数量积(1)(2)(3)(4)性质2.空间向量的坐标运算.1.设 为两两垂直的单位向量,如果 , 则 叫做向量的坐标,也叫做点 的坐标.2.则3.空间向量在解题中的作用(1) 证明线线平行,线面平行,线线垂直,线面垂直.(2) 求线线角,线面角,面面角.八.直线与平面成的角.1.平面的斜线和平面成的角C平面的斜线和它在平面内的射影成的角,是这条斜线和这个平面内任一条直线所成的角中最小的角.定义: 一个平面的斜线和它在这个平面内的射影的夹角,叫做斜线和平面所成的角.如果直线和平面垂直那么就说直线和平面所成的角是直角.如果直线和平面平行或在平面内,就说直线和平面所成的角是00的角.1.直线AB与直二面角 的两个半平面分别交于A、B两点,且A,B ,画出直线AB与 和 所成的角,并讨论
的取值范围.练习:九. 空间距离1.点到平面的距离2.点到直线的距离3.异面直线间的距离当垂足不易确定时,常用等体积法求点到平面的距离完
E是BB1上的点。画出平面AEC1
和平面ABCD的交线。
一、平面的基本性质 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理1用来判定一条直线是否在平面
内,或直线上的点是否在平面内。
F作用
如果两个平面有一个公共点,那么它们还有其他公共
点,且所有这些公共点的集合是一条过这个公共点的直线. 公理21、用来判定两平面是否相交;
2、画两个相交平面的交线;
即:
3、证明多点共线.练习2: 已知ΔABC在平面α外,AB、AC、BC的延长线分别与平面α交于点M、N、P三
点,求证:M、N、P三点共线。
作用
,1、确定平面
2、证明点、线共面。公理3:经过不在同一条直线上的三点,有且只有一个平面。作用
推论1.一条直线和直线外一点唯一确定一个平面。推论2.两条相交直线唯一确定一个平面。推论3.两条平行直线唯一确定一个平面。例1:已知三条直线l1 , l2 , l3 两两相交,且不过同一点,求证:直线l1 , l2, l3 在同一平面内。例2:直线L与过点P的三条直线a1 , a2 , a3 分别交于
A,B,C三点(A,B,C异于点P),求证:这四
条直线共面。二、空间两直线的位置关系平行相交异面共面(两直线没有公共点)(两直线只有一个公共点)(两直线没有公共点) 不同在任何一个平面内的两条直线叫做异面直线。(也就是既不相交又不平行的两条直线)1、异面直线OEFEFAE和BF是异面直线吗?AE和CF是异面直线吗?2.异面直线的画法:通常用一个或两个平面来衬托异面直线不同在任何一个平面的特点
θθ如图所示, a、b 是两条异面直线,在空间中任选一点O,过O点分别作 a、b的平行线 a′和 b′,则a′和 b′所成的锐角θ, (或直角),称为异面直线a,b所成的角,也叫异面直线a,b 的夹角。aba′b′ 若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移3.异面直线成的角:O4.求异面直线所成的角:求两条异面直线所成角的步骤:1.选点,引平行线找到所求的角;2.把该角放入三角形;3.根据边角关系计算,求角.例1.正方体ABCD-A1B1C1D1中,E,F分别是BB1,CC1的中点,求AE,BF所成的角在解答过程中要突出“做、证、指、求”这几步。例2:
已知正方体的棱长为a , M 为 AB 的中点, N为 BB1的中点,求 A1M 与 C1 N 所成角的余弦值。解:如图,取A1B1的中点E, 连BE, 有BE∥ A1M 取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角。BG=BE= a, EG = a由余弦定理,cos∠EBG=2/5取EB1的中点F,连NF,有BE∥NF则∠FNC1为所求角。想一想:还有其它定角的方法吗?在△EBG中EG例3.在空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC,AD的中点,求异面直线AM,CN所成角。EG例5.长方体ABCD-A1B1C1D1中,AB=2, BC=1,AA1 =1,求异面直线D1B与AC所成角的余弦值.GAB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?相交直线有几对?平行直线有几对?若a∥b,b∥c,公理4 平行于同一直线的两直线互相平行则a∥c5.平行关系的传递性例1:在正方体ABCD—A1B1C1D1中,直线 AB与C1D1 ,AD1与 BC1 是什么位置关系?为什么?例2 已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。解题思想:把所要解的立体几何问题
转化为平面几何的问题是解立体几何时最主要、最常用的一种方法。6.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。 右图平行六面体中与∠BAD相等的角是哪些角,为什么?
与∠BAD互补的角是哪些,为什么?
填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。平行相交异面平行异面无数无数相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( ) ????判断对错:思考题:
1、a与b是异面直线,且c∥a,则c与b一定( )。
(A)异面 (B)相交 (C)平行 (D)不平行
2、正方体一条对角线与正方体的棱可组成的异面直线的对数
是( )对。
(A)6 (B)3 (C)8 (D)12
3、一条直线和两条异面直线都相交,则它们可以确定( )
平面。
(A)一个 (B)两个 (C)三个 (D)四个三、直线和平面平行的判定和性质定理1.直线和平面的位置关系有哪些?(1)直线在平面内:(2)直线与平面相交:(3)直线与平面平行:2.直线和平面平行的判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)证明直线与平面平行的方法是什么?思考1.在平面内寻找一条直线 2.证明这条直线与已知直线平行.3.直线和平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面与已知平面相交,那么这条直线与交线平行. (线面平行,线线平行)练习:如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个平面垂直。2.直线和平面垂直的判定定理:线不在多,重在相交! 如果一条直线与一个平面内任何一条直线都垂直,我们就说这条直线与这个平面相互垂直。1.直线和平面垂直的定义:四.直线和平面垂直的判定和性质判断对错 ?3.直线和平面垂直的性质定理:性质1如果一条直线垂直于一个平面,那么这条直线垂直于平面的任意一条直线.性质2如果两条平行线中的一条与平面垂直,那么另一条也与这个平面垂直.线线垂直— 线面垂直—线线垂直常用方法例2. 在正方体AC1中,取DD1
的中点E,AC和BD交于O点。 求证:OB1⊥面EAC4.三垂线定理:正射影自一点P向平面 引垂线,垂足Q叫做点P在平面 上的正射影.(简称射影)如果图形F上的所有点在一平面内的射影构成图形F1,则F1叫做图形F在这个平面内的射影.F1O三垂线定理在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直 .三垂线定理的逆定理O在平面内的一条直线,如果它和这个平面的一条斜线垂直, 那么它也和这条斜线的射影垂直 .练习1.如图 为矩形,
由三垂线定理可得到哪些线是垂直的?OEFG2.四面体ABCD中,AB DC
AD BC,求证:AC BDD3.直角三角形ABC中,角C为直角,AC=2,BC= ,PC 平面BCD,PC=3。求点P到直线AB的距离。五.两个平面平行的判定和性质1.空间两个平面的位置关系两个平面平行两个平面相交2. 两个平面平行的判定定理如果一个平面的两条相交直线都与另一个平面平行,那么这两个平面平行。3. 两个平面平行的性质定理1.如果两个平行平面和第三个平面都相交,那么交线互相平行2.如果两个平面平行,那么其中一个平面内的任何一条直线都平行于另一个平面。六.两个平面垂直的判定和性质1. 两个平面垂直的定义(1) 二面角平面内的一条直线把平面分为两部分,其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,每个半平面叫做二面角的面.如图,二面角及表示方法.二面角C-AB- D二面角?-AB- ?二面角(2) 二面角的平面角二面角的大小用它的平面角来度量注意:二面角的平面角必须满足:3)角的边都要垂直于二面角的棱1)角的顶点在棱上2)角的两边分别在两个面内4)二面角的范围是以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角(3) 两个平面垂直的定义:如果两个平面所成的二面角是直二面角,那么就称这两个平面互相垂直.101.利用定义.(4) 二面角的平面角的作法3.作棱的垂面.2.利用三垂线定理及其逆定理.练习:作出下列各图中的二面角的平面角:二面角B—B1C—A OEO二面角A--BC--D二面角C--AD--E四棱锥中取AB 的中点为E,连PE,OE∵O为 AC 中点, ∠ABC=90o∴OE∥BC且 OE BC在Rt△POE中, OE ,PO ∴∴所求的二面角P-AB-C 的正切值为例1.如图,三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O,若PB=AB=1,BC= ,求二面角P-AB-C的正切值。∴∠PEO为二面角P-AB-C 的平面角在Rt△PBE中,BE ,PB=1,PE由三垂线定理知 PE⊥AB解:∴ OE⊥AB ,做证指求答3. 两个平面垂直的性质定理如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面2. 两个平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.七.空间向量.1.空间向量及运算.1.在空间,我们把具有大小和方向的量叫做向量.2.空间向量也用有向线段表示,并且同向且等长的 有向线段表示同一个向量.4.平行于同一个平面的向量叫做共面向量.3.在空间,如果表示向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量.5.共线向量定理:对空间任意两个向量 和 , 的充要条件是存在实数 ,使 .6.共面向量定理:如果两个向量
和 不共线, 则向量 与向量
, 共面的充要条件是存在实数
,使 .8. 空间向量基本定理:9.空间向量的数量积(1)(2)(3)(4)性质2.空间向量的坐标运算.1.设 为两两垂直的单位向量,如果 , 则 叫做向量的坐标,也叫做点 的坐标.2.则3.空间向量在解题中的作用(1) 证明线线平行,线面平行,线线垂直,线面垂直.(2) 求线线角,线面角,面面角.八.直线与平面成的角.1.平面的斜线和平面成的角C平面的斜线和它在平面内的射影成的角,是这条斜线和这个平面内任一条直线所成的角中最小的角.定义: 一个平面的斜线和它在这个平面内的射影的夹角,叫做斜线和平面所成的角.如果直线和平面垂直那么就说直线和平面所成的角是直角.如果直线和平面平行或在平面内,就说直线和平面所成的角是00的角.1.直线AB与直二面角 的两个半平面分别交于A、B两点,且A,B ,画出直线AB与 和 所成的角,并讨论
的取值范围.练习:九. 空间距离1.点到平面的距离2.点到直线的距离3.异面直线间的距离当垂足不易确定时,常用等体积法求点到平面的距离完
