人教版八年级数学下册课件-18.2.1 矩形 (共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件-18.2.1 矩形 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-02 08:17:00 | ||
图片预览



文档简介
课件19张PPT。18.2.1 矩形第十八章 平行四边形人教版
八年级
下册新课引入 1、平行四边形的性质有:平行四边形的对边
______________;对角_______;邻角______;
对角线__________________.
2、平行四边形的判定方法有:
两组对边____________
两组对边____________
一组对边____________ 的四边形是平行四边形
两组对角____________
对角线______________平行且相等 相等 互补 互相平分 分别相等 分别相等 平行且相等 分别相等 互相平分 平行相等平行相等相等相等平分平分相等新课引入 12学习目标 理解矩形定义; 掌握矩形的性质. 3掌握矩形的判定方法. 新课讲解知识点一 矩形的定义和性质
1、矩形的定义: 的平行四边形是矩形.
有一个角是直角
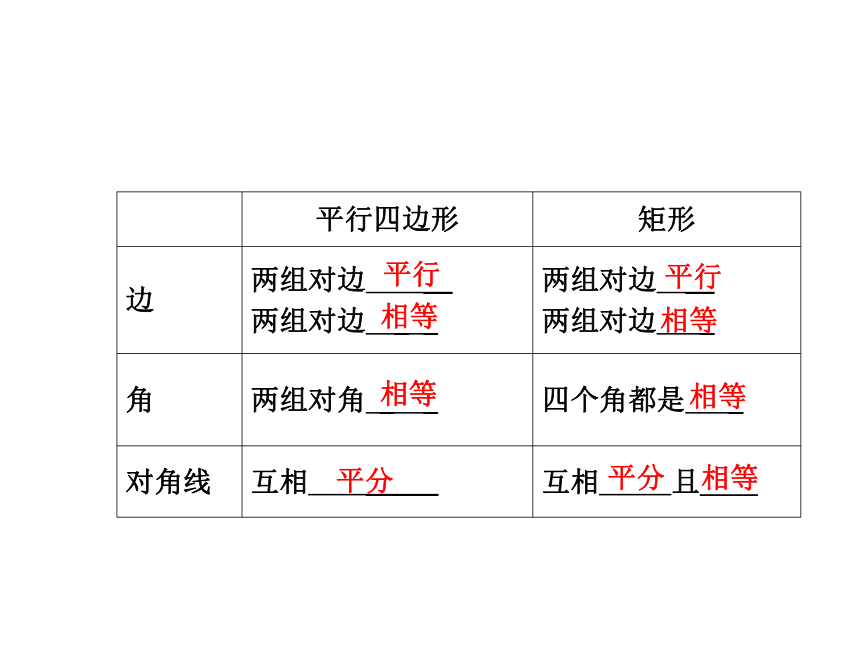
2、矩形的性质
(1)矩形是特殊的 形,它具有 形
的一切性质.即边: ;
角: ;
对角线: .
(2)矩形还有以下特殊性质:
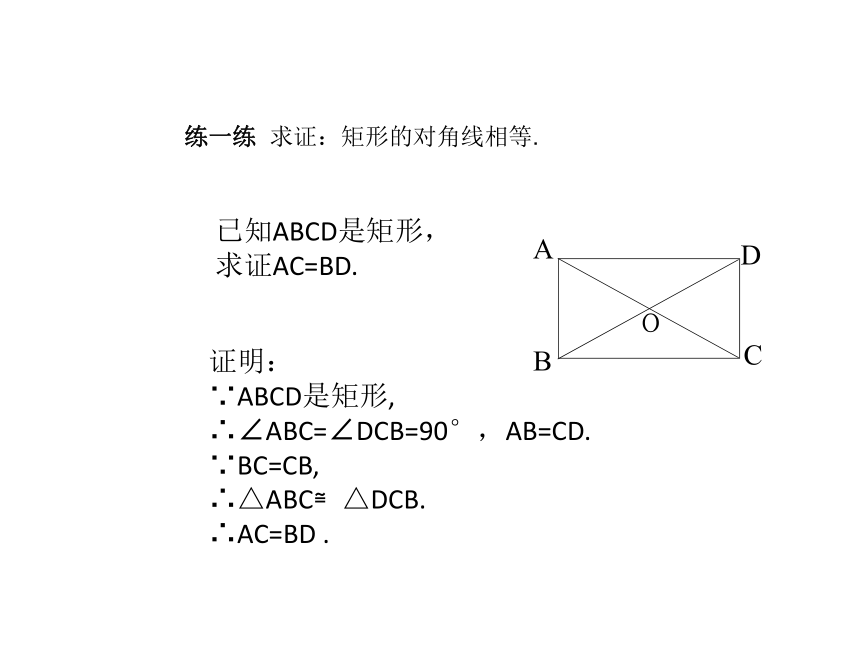
① ② .知识点一有一个角是直角 平行四边 平行四边 矩形的对边平行且相等 矩形的对角相等 矩形的对角线互相平分 矩形的四个角都是直角 矩形的对角线相等 练一练 求证:矩形的对角线相等.已知ABCD是矩形, 求证AC=BD. 证明: ∵ABCD是矩形, ∴∠ABC=∠DCB=90°,AB=CD. ∵BC=CB, ∴△ABC≌△DCB. ∴AC=BD .新课讲解知识点二 矩形性质的应用
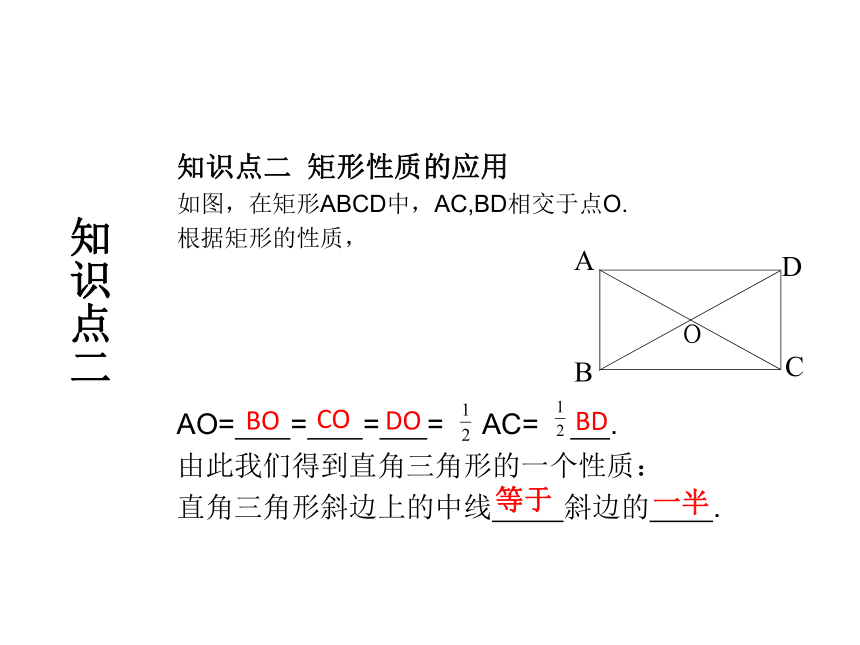
如图,在矩形ABCD中,AC,BD相交于点O.
根据矩形的性质,
AO= = = = AC= .
由此我们得到直角三角形的一个性质:
直角三角形斜边上的中线 斜边的 .知识点二BO CO DO BD 等于 一半 新课讲解例1 如图,矩形ABCD的对角线AC、BD相
交于点O, ∠AOB= 60°,AB=4 ,求矩形对
角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD 且 .
∴OA=OB,
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA=OB= .
∴AC=BD=2 = .知识点三相等 互相平分 等边 AB AB 2×4=8 新课讲解2、矩形是轴对称图形吗?如果是,它有几条
对称轴?知识点三答:是,有两条对称轴 。新课讲解练一练
1、一个矩形的一条对角线长为8,两条对角
线的一个交角为120°.
求这个矩形的边长(结果保留小数点后两位).知识点三新课讲解 矩形的判定定理
知识点四:1、(定义) 的平行四边形是矩形.
符号语言,如图,在口ABCD中,
∵∠ =90°
∴口ABCD是 .有一个角是直角A平行四边形新课讲解 矩形的判定定理
知识点一:2、对角线_________ 是矩形.
已知: 如图,在口ABCD中, ___ ,
求证:平行四边形ABCD是矩形.证明:∵四边形ABCD是 ___ ,
∴AB= ,BC= ,
又∵AC= ,
∴△ABC≌△DCB.
∴∠ABC=∠DCB.
又∵ ∥ ,
∴∠ABC+∠DCB=180°.∴∠ABC=∠DCB= .
∴口ABCD是矩形.(有一个角是_______的平行四边形是_______)互相平分且相等的平行四边形AC=BD平行四边形CDADBDABCD直角矩形新课讲解 矩形判定定理的应用
知识点二:如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=
∴∠AOD=
又AO=DO
∴∠ADC=
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为新课讲解1、矩形的定义:_______________________
____________________________________;
2、矩形的特殊性质:___________________
____________________________________
____________________________________;
3、直角三角形斜边上的中线等于__________
____________________________________.
4、学习反思:________________________
___________________________. 有一个角是直角的平行四边形是矩形; 矩形的四个角都是直角
矩形的对角线相等 斜边的一半 归纳小结1、矩形的判定定理:
(1)(定义)________________________________;
(2)______________________________________;
(3)__________________________________.
2、矩形判定定理的应用.
有一个角是直角的平行四边形是矩形对角线互相平分且相等的平行四边形是矩形有三个角是直角的四边形是矩形归纳小结强化训练 1、矩形两条对角线把矩形分成 个等腰
三角形.2、矩形具有而平行四边形不一定具有的性
质是 (填代号)
①对边平行且相等;②对角线互相平分;
③对角相等; ④对角线相等;
⑤4个角都是90°;⑥轴对称图形四 ④ ⑤ ⑥ 4、矩形的两条对角线所成的钝角为120°,
若一条对角线的长是2,那么它的周长是 。3、矩形的面积为48,一条边长为6,则矩形的另
一边长为 ,对角线为 .810强化训练 5、判断正误:
(1)有一个角是直角的四边形是矩形. ( )
(2)对角线相等的四边形是矩形. ( )
(3)对角线互相平分且相等的四边形是矩形.( )
(4)四个角都相等的四边形是矩形. ( )
(5)一组邻角相等的平行四边形是矩形.( )
(6)对角互补的平行四边形是矩形. ( )
×××√√√强化训练 6、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形强化训练
八年级
下册新课引入 1、平行四边形的性质有:平行四边形的对边
______________;对角_______;邻角______;
对角线__________________.
2、平行四边形的判定方法有:
两组对边____________
两组对边____________
一组对边____________ 的四边形是平行四边形
两组对角____________
对角线______________平行且相等 相等 互补 互相平分 分别相等 分别相等 平行且相等 分别相等 互相平分 平行相等平行相等相等相等平分平分相等新课引入 12学习目标 理解矩形定义; 掌握矩形的性质. 3掌握矩形的判定方法. 新课讲解知识点一 矩形的定义和性质
1、矩形的定义: 的平行四边形是矩形.
有一个角是直角
2、矩形的性质
(1)矩形是特殊的 形,它具有 形
的一切性质.即边: ;
角: ;
对角线: .
(2)矩形还有以下特殊性质:
① ② .知识点一有一个角是直角 平行四边 平行四边 矩形的对边平行且相等 矩形的对角相等 矩形的对角线互相平分 矩形的四个角都是直角 矩形的对角线相等 练一练 求证:矩形的对角线相等.已知ABCD是矩形, 求证AC=BD. 证明: ∵ABCD是矩形, ∴∠ABC=∠DCB=90°,AB=CD. ∵BC=CB, ∴△ABC≌△DCB. ∴AC=BD .新课讲解知识点二 矩形性质的应用
如图,在矩形ABCD中,AC,BD相交于点O.
根据矩形的性质,
AO= = = = AC= .
由此我们得到直角三角形的一个性质:
直角三角形斜边上的中线 斜边的 .知识点二BO CO DO BD 等于 一半 新课讲解例1 如图,矩形ABCD的对角线AC、BD相
交于点O, ∠AOB= 60°,AB=4 ,求矩形对
角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD 且 .
∴OA=OB,
又∠AOB= 60°,
∴△OAB是 三角形.
∴OA=OB= .
∴AC=BD=2 = .知识点三相等 互相平分 等边 AB AB 2×4=8 新课讲解2、矩形是轴对称图形吗?如果是,它有几条
对称轴?知识点三答:是,有两条对称轴 。新课讲解练一练
1、一个矩形的一条对角线长为8,两条对角
线的一个交角为120°.
求这个矩形的边长(结果保留小数点后两位).知识点三新课讲解 矩形的判定定理
知识点四:1、(定义) 的平行四边形是矩形.
符号语言,如图,在口ABCD中,
∵∠ =90°
∴口ABCD是 .有一个角是直角A平行四边形新课讲解 矩形的判定定理
知识点一:2、对角线_________ 是矩形.
已知: 如图,在口ABCD中, ___ ,
求证:平行四边形ABCD是矩形.证明:∵四边形ABCD是 ___ ,
∴AB= ,BC= ,
又∵AC= ,
∴△ABC≌△DCB.
∴∠ABC=∠DCB.
又∵ ∥ ,
∴∠ABC+∠DCB=180°.∴∠ABC=∠DCB= .
∴口ABCD是矩形.(有一个角是_______的平行四边形是_______)互相平分且相等的平行四边形AC=BD平行四边形CDADBDABCD直角矩形新课讲解 矩形判定定理的应用
知识点二:如图,口ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4.求口ABCD的面积.解:∵△OAB是等边三角形且四边形ABCD的对角线AC、BD互相平分
∴AO=OB=OC=OD=AB=DC=4
∵∠AOB=
∴∠AOD=
又AO=DO
∴∠ADC=
∴四边形ABCD是矩形
AC=8 ,DC=4, AD=
∴平行四边形ABCD面积为新课讲解1、矩形的定义:_______________________
____________________________________;
2、矩形的特殊性质:___________________
____________________________________
____________________________________;
3、直角三角形斜边上的中线等于__________
____________________________________.
4、学习反思:________________________
___________________________. 有一个角是直角的平行四边形是矩形; 矩形的四个角都是直角
矩形的对角线相等 斜边的一半 归纳小结1、矩形的判定定理:
(1)(定义)________________________________;
(2)______________________________________;
(3)__________________________________.
2、矩形判定定理的应用.
有一个角是直角的平行四边形是矩形对角线互相平分且相等的平行四边形是矩形有三个角是直角的四边形是矩形归纳小结强化训练 1、矩形两条对角线把矩形分成 个等腰
三角形.2、矩形具有而平行四边形不一定具有的性
质是 (填代号)
①对边平行且相等;②对角线互相平分;
③对角相等; ④对角线相等;
⑤4个角都是90°;⑥轴对称图形四 ④ ⑤ ⑥ 4、矩形的两条对角线所成的钝角为120°,
若一条对角线的长是2,那么它的周长是 。3、矩形的面积为48,一条边长为6,则矩形的另
一边长为 ,对角线为 .810强化训练 5、判断正误:
(1)有一个角是直角的四边形是矩形. ( )
(2)对角线相等的四边形是矩形. ( )
(3)对角线互相平分且相等的四边形是矩形.( )
(4)四个角都相等的四边形是矩形. ( )
(5)一组邻角相等的平行四边形是矩形.( )
(6)对角互补的平行四边形是矩形. ( )
×××√√√强化训练 6、如图AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:∵ABCD是矩形,
∴OA=OC,OB=OD
OE=OA-AE,OG=OC-CG
∵AE=CG
∴OE=OG
OF=OB-OD,OH=OD-DH
∵BF=DH
∴OF=OH
∴四边形EFGH是平行四边形
∵ABCD是矩形,
∴AC=BD
EG=AC-AE-CG
FH=BD-BF-DH
∴EG=FH
∴平行四边形EFGH是矩形强化训练
