人教版七年级数学上册第四章几何初步4.2.2直线、射线与线段 线段的性质课件
文档属性
| 名称 | 人教版七年级数学上册第四章几何初步4.2.2直线、射线与线段 线段的性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 303.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-02 00:00:00 | ||
图片预览




文档简介
课件18张PPT。4.2 直线、射线、线段
第三课时人教版七年级数学线段的性质你能用这根绳子正好做一双鞋带吗?探究一AB点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.看一看说一说如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.文字叙述:数学符号语言: 因为点M是线段AB的中点
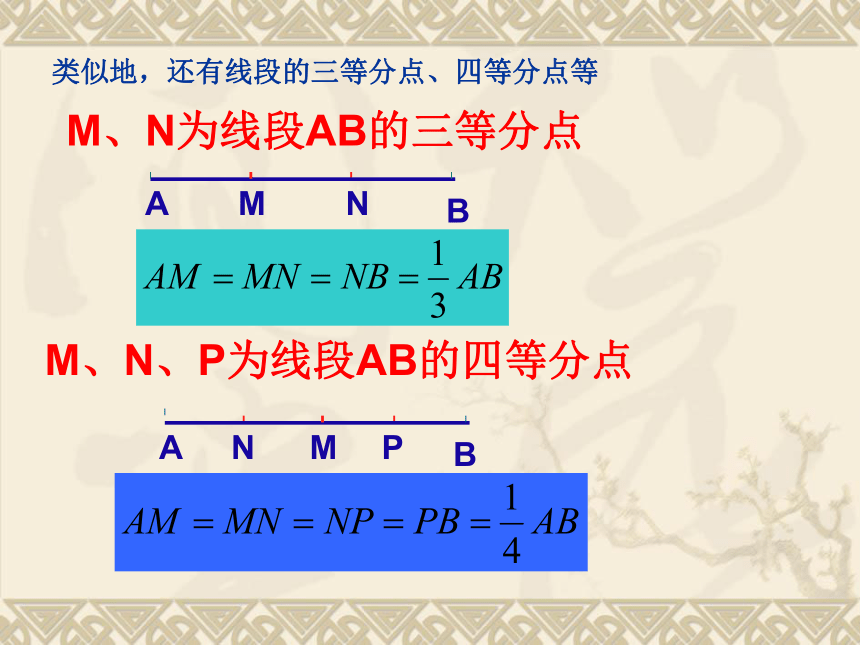
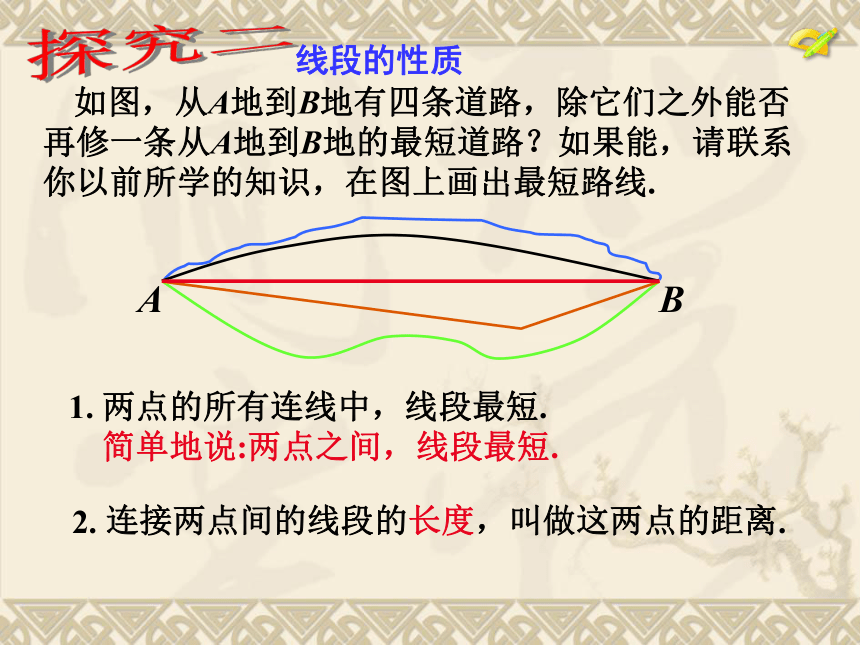
所以AM=MB= AB,AB=2AM=2BMABMNABMM、N为线段AB的三等分点NPM、N、P为线段AB的四等分点类似地,还有线段的三等分点、四等分点等如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP=1.5cm,求线段AB的长等于______.ABA思维测评9cm如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 1. 两点的所有连线中,线段最短.
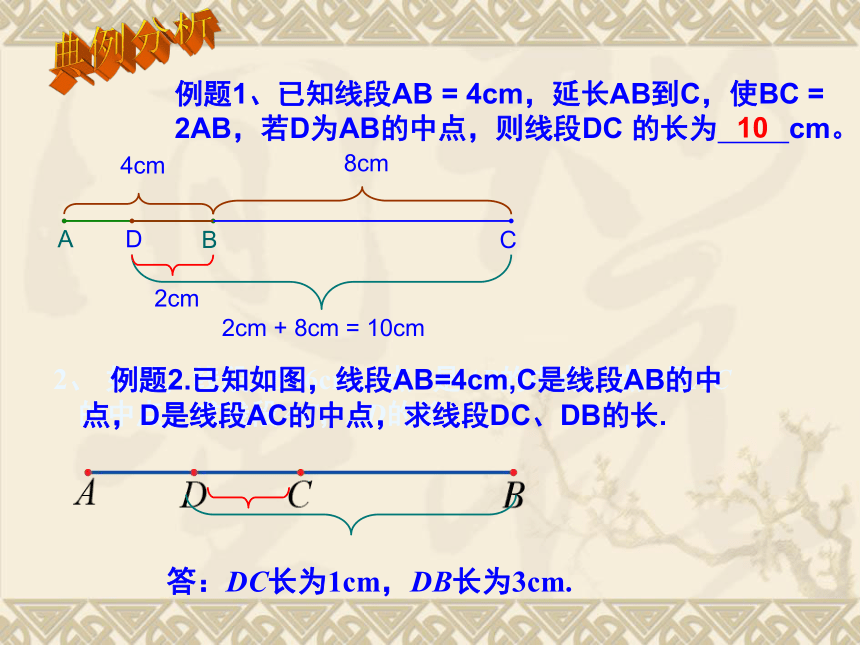
简单地说:两点之间,线段最短. 2. 连接两点间的线段的长度,叫做这两点的距离.探究二线段的性质 2、 如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.答:DC长为1cm,DB长为3cm.例题1、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。ABCD4cm8cm2cm2cm + 8cm = 10cm10 例题2.已知如图,线段AB=4cm,C是线段AB的中
点,D是线段AC的中点,求线段DC、DB的长.典例分析例题3. 如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( ) A.5 B.2.5 C.5或2.5 D.5或1
解析:本题有两种情形:
(1)当点C在线段AB上时,如图:
AC=AB-BC,又∵AB=6,BC=4,
∴AC=6-4=2,D是AC的中点,∴AD=1;
(2)当点C在线段AB的延长线上时,如图:
AC=AB+BC,又∵AB=6,BC=4,∴AC=6+4=10,D是AC的中点,∴AD=5.故选D.解答本题关键是正确画图,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解例题4、如图,把弯曲的河道改直,能够缩短航程,这样做的根据是( )
A.两点之间,直线最短
B.两点确定一条线段
C.两点确定一条直线
D.两点之间,线段最短
方法总结:本题考查了线段的性质,熟记两点之间线段最短是解题的关键 1.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以AM=MB=AB;
④因为A、M、B在同一条直线上,且AM=BM,所以M是AB的中点,
其中正确的是( ).
A.①③④ B.④ C.②③④ D.③④巩固训练,深化提高2、下列说法正确的是( )
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度,叫做两点间的距离
C、连结两点的直线的长度,叫做两点的距离
D、连结两点的线段的长度,叫做两点间的距离D3、如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm根据线段的中点表示出线段的长,再根据线段的和、差求未知线段的长度 解析:点M是AC的中点,点N是BC的中点,∴AC=2MC,BC=2NC,∴AC-BC=(MC-NC)×2=4cm,即AC比BC长4cm,故选B 4、 如图,B、C两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求: (1)AD的长;(2)AB∶BE.
解:(1)设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得ED=?AD=4.5x.
由线段的和差得
CE=DE-CD=4.5x-4x=0.5X=2.
解得x=4.∴AD=9x=36(cm);
(2)AB=2x=8(cm),BC=3x=12(cm).
由线段的和差,得BE=BC-CE=12-2=10(cm).
∴AB∶BE=8∶10=4∶5.解析:(1)根据线段的比,可设出未知数,根据线段的和差,可得方程,根据解方程,可得x的值,根据x的值,可得AD的长度;
(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案方法总结:在遇到线段之间比的问题时,往往设出未知数,列方程解答 1、有A、B、C三个城市,已知A、B两城市的距离为50千米,B、C两城市的距离为 30 千米,那么A、C两城市的距离是( )
A、80千米 B、20千米
C、40千米 D、处于20千米到80千米间
当堂达标两点之间线段最短2、如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
3、 有条小河L,点A,B表示在河两岸的两个村庄,现在要建造一座小桥,请你找出造桥的位置,使得A,B两村的路程最短,并说明理由。LAB桥4、问:若要在西湖风景区建造一个消费场所,为了方便游客,要求是到图中四个红色的旅游区的距离之和最短,请问应该建造在何处?如图,线段AB与线段CD的交点E为所求的点,即消费场所建在E点位置最合适。学科网了解了线段性质在生活中的运用,
体会到数学就在我们身边。
第三课时人教版七年级数学线段的性质你能用这根绳子正好做一双鞋带吗?探究一AB点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.看一看说一说如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.文字叙述:数学符号语言: 因为点M是线段AB的中点
所以AM=MB= AB,AB=2AM=2BMABMNABMM、N为线段AB的三等分点NPM、N、P为线段AB的四等分点类似地,还有线段的三等分点、四等分点等如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP=1.5cm,求线段AB的长等于______.ABA思维测评9cm如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 1. 两点的所有连线中,线段最短.
简单地说:两点之间,线段最短. 2. 连接两点间的线段的长度,叫做这两点的距离.探究二线段的性质 2、 如图,线段AB=6cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.答:DC长为1cm,DB长为3cm.例题1、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。ABCD4cm8cm2cm2cm + 8cm = 10cm10 例题2.已知如图,线段AB=4cm,C是线段AB的中
点,D是线段AC的中点,求线段DC、DB的长.典例分析例题3. 如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( ) A.5 B.2.5 C.5或2.5 D.5或1
解析:本题有两种情形:
(1)当点C在线段AB上时,如图:
AC=AB-BC,又∵AB=6,BC=4,
∴AC=6-4=2,D是AC的中点,∴AD=1;
(2)当点C在线段AB的延长线上时,如图:
AC=AB+BC,又∵AB=6,BC=4,∴AC=6+4=10,D是AC的中点,∴AD=5.故选D.解答本题关键是正确画图,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解例题4、如图,把弯曲的河道改直,能够缩短航程,这样做的根据是( )
A.两点之间,直线最短
B.两点确定一条线段
C.两点确定一条直线
D.两点之间,线段最短
方法总结:本题考查了线段的性质,熟记两点之间线段最短是解题的关键 1.下列四种说法:
①因为AM=MB,所以M是AB中点;
②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;
③因为M是AB的中点,所以AM=MB=AB;
④因为A、M、B在同一条直线上,且AM=BM,所以M是AB的中点,
其中正确的是( ).
A.①③④ B.④ C.②③④ D.③④巩固训练,深化提高2、下列说法正确的是( )
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度,叫做两点间的距离
C、连结两点的直线的长度,叫做两点的距离
D、连结两点的线段的长度,叫做两点间的距离D3、如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如MC比NC长2cm,AC比BC长( )
A.2cm B.4cm C.1cm D.6cm根据线段的中点表示出线段的长,再根据线段的和、差求未知线段的长度 解析:点M是AC的中点,点N是BC的中点,∴AC=2MC,BC=2NC,∴AC-BC=(MC-NC)×2=4cm,即AC比BC长4cm,故选B 4、 如图,B、C两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求: (1)AD的长;(2)AB∶BE.
解:(1)设AB=2x,则BC=3x,CD=4x,
由线段的和差,得AD=AB+BC+CD=9x.
由E为AD的中点,得ED=?AD=4.5x.
由线段的和差得
CE=DE-CD=4.5x-4x=0.5X=2.
解得x=4.∴AD=9x=36(cm);
(2)AB=2x=8(cm),BC=3x=12(cm).
由线段的和差,得BE=BC-CE=12-2=10(cm).
∴AB∶BE=8∶10=4∶5.解析:(1)根据线段的比,可设出未知数,根据线段的和差,可得方程,根据解方程,可得x的值,根据x的值,可得AD的长度;
(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案方法总结:在遇到线段之间比的问题时,往往设出未知数,列方程解答 1、有A、B、C三个城市,已知A、B两城市的距离为50千米,B、C两城市的距离为 30 千米,那么A、C两城市的距离是( )
A、80千米 B、20千米
C、40千米 D、处于20千米到80千米间
当堂达标两点之间线段最短2、如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
3、 有条小河L,点A,B表示在河两岸的两个村庄,现在要建造一座小桥,请你找出造桥的位置,使得A,B两村的路程最短,并说明理由。LAB桥4、问:若要在西湖风景区建造一个消费场所,为了方便游客,要求是到图中四个红色的旅游区的距离之和最短,请问应该建造在何处?如图,线段AB与线段CD的交点E为所求的点,即消费场所建在E点位置最合适。学科网了解了线段性质在生活中的运用,
体会到数学就在我们身边。
