七年级上5.3展开与折叠同步练习(解析版)
文档属性
| 名称 | 七年级上5.3展开与折叠同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-03 00:00:00 | ||
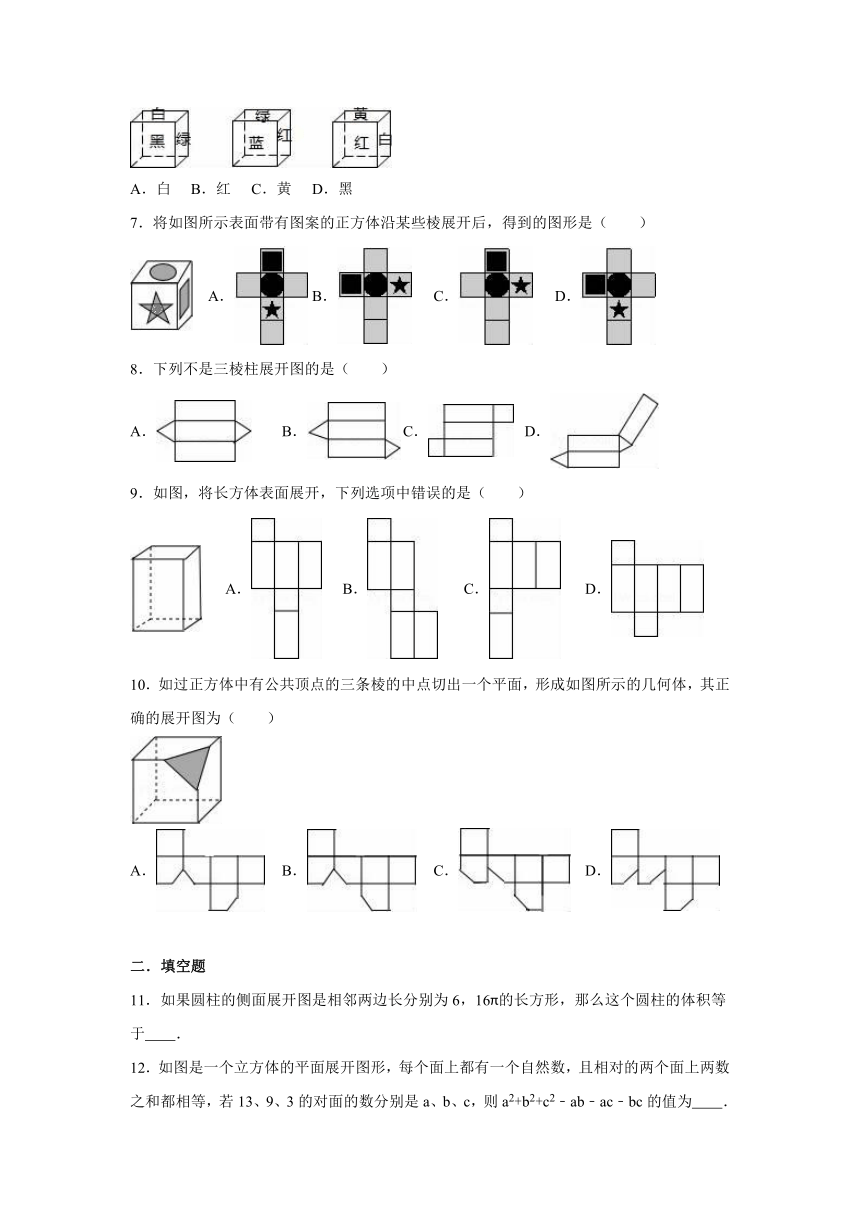
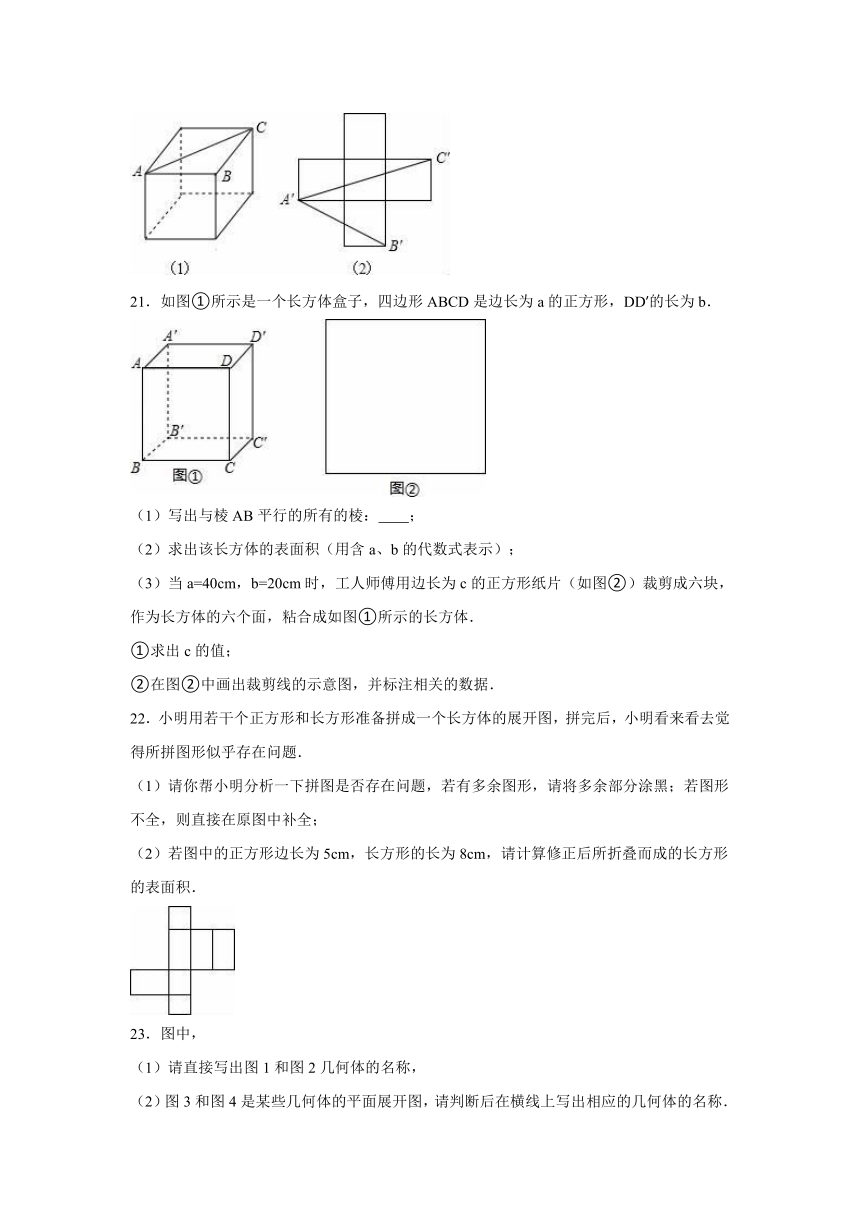
图片预览



文档简介
5.3
展开与折叠
一.选择题
1.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇
B.见
C.未
D.来
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
3.下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
5.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
6.有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白
B.红
C.黄
D.黑
7.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
8.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
9.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
10.如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
A.
B.
C.
D.
二.填空题
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2﹣ab﹣ac﹣bc的值为 .
13.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 种拼接方法.
14.一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是 .
15.如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是 .
三.解答题
16.将图中剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去几号小正方形?写出所有可能的情况.
17.如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
18.如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
19.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
20.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
22.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方形的表面积.
23.图中,
(1)请直接写出图1和图2几何体的名称,
(2)图3和图4是某些几何体的平面展开图,请判断后在横线上写出相应的几何体的名称.
24.如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
26.如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 .
参考答案与解析
一.选择题
1.(2016 达州)如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇
B.见
C.未
D.来
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“遇”与“的”是相对面,
“见”与“未”是相对面,
“你”与“来”是相对面.
故选D.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2016 资阳)如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴C符合题意.
故选C.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.(2016 徐州)下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
【分析】利用不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况进行判断也可.
【解答】A.可以作为一个正方体的展开图,
B.可以作为一个正方体的展开图,
C.不可以作为一个正方体的展开图,
D.可以作为一个正方体的展开图,
故选;C.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.(2016 绍兴)如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
【分析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
【解答】解:A、含有田字形,不能折成正方体,故A错误;
B、能折成正方体,故B正确;
C、凹字形,不能折成正方体,故C错误;
D、含有田字形,不能折成正方体,故D错误.
故选:B.
【点评】本题主要考查的是几何体的展开图,明确含有田字形和凹字形的图形不能折成正方体是解题的关键.
5.(2016 河北)图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.
【解答】解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,故选:A.
【点评】本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
6.(2016 枣庄)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白
B.红
C.黄
D.黑
【分析】根据图形可得涂有绿色一面的邻边是白,黑,红,蓝,即可得到结论.
【解答】解:∵涂有绿色一面的邻边是白,黑,红,蓝,
∴涂成绿色一面的对面的颜色是黄色,
故选C.
【点评】本题考查了正方体相对两个面上的文字问题,此类问题可以制作一个正方体,根据题意在各个面上标上图案,再确定对面上的图案,可以培养动手操作能力和空间想象能力.
7.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点.
【解答】解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选C.
【点评】考查了几何体的展开图,解决此类问题,要充分考虑带有各种符号的面的特点及位置.
8.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
【分析】根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【解答】解:∵三棱柱展开图有3个四边形,2个三角形,
∴C选项不是三棱柱展开图,
故选:C.
【点评】本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
9.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
【分析】长方体的表面展开图的特点,有四个长方形的侧面和上下两个底面组成.
【解答】解:A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选:C.
【点评】本题考查的是长方体的展开图,关键是要注意上下底面的长和宽是否可以围成长方体.
10.如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:选项A、C、D折叠后都不符合题意,只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去三角形交于一个顶点符合.
故选:B.
【点评】考查了截一个几何体和几何体的展开图.解决此类问题,要充分考虑带有各种符号的面的特点及位置.
二.填空题
11.(2016 云南)如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
12.如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2﹣ab﹣ac﹣bc的值为 76 .
【分析】本题须先求出a﹣b=﹣4,b﹣c=﹣6,c﹣a=10,再通过对要求的式子进行化简整理,代入相应的值即可求出结果.
【解答】解:∵正方体的每一个面上都有一个正整数,相对的两个面上两数之和都相等,
∴a+13=b+9=c+3,
∴a﹣b=﹣4,b﹣c=﹣6,c﹣a=10,
a2+b2+c2﹣ab﹣bc﹣ca=
=
=
=76
故答案为:76.
【点评】本题主要考查了整式的混合运算﹣化简求值问题,在解题时要注意知识的综合运用及与图形结合问题.
13.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 4 种拼接方法.
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
【点评】此题主要考查了几何体的展开图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
14.一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是 碳 .
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“低”与“绿”是相对面,
“碳”与“保”是相对面,
“环”与“色”是相对面.
故答案为:碳.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
15.如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是 B、C、E、F .
【分析】根据正方体展开图的11种特征,本题属于正方体展开图的“141”结构,把它折成正方体后,A面与D面相对,其余的面都与A面垂直.
【解答】解:因为正方体的表面展开图,相对的面之间一定相隔一个正方形,面“A”与“D”是相对面,它们互相平行,剩下的面都与A面垂直;
所以:围成正方体盒子,与面A垂直的面用图中字母表示出来是:B、C、E、F;
故答案为:B、C、E、F.
【点评】本题考查了展开图折叠成几何体,注意正方体的空间图形,从相对面入手,分析及解答问题.
三.解答题
16.将图中剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去几号小正方形?写出所有可能的情况.
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:根据有“田”字格的展开图都不是正方体的表面展开图可知:应剪去1或2或3.
【点评】此题主要考查了正方体展开图,关键是掌握正方体展开图的特点,中间四联方,上下各一个.
17.如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
【分析】此题的关键是找出正方体的相对面,仔细观察会发现3与x是相对面,3﹣2y与y是相对面,z+4与1﹣2x是相对面,根据这个正方体纸盒相对的两个面上的代数式的值相等,求出x,y,z的值.
【解答】解:根据题意得:
解得:.
【点评】考查了正方体相对两个面上的文字,做这类题学生要养成仔细观察并动脑的习惯.
18.如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
【分析】(1)根据几何体的三视图,可得出几何体是六棱柱;
(2)由图可得侧面积等于六个矩形的面积.
【解答】解:(1)这个几何体的名称是六棱柱;
(2)侧面积=(2+4)ab=6ab.
【点评】本题考查了由三视图判断几何体以及几何体的表面积,几何体的侧面积等于六个矩形的面积.
19.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
【分析】(1)根据平面图形得出剪开棱的条数,
(2)根据长方体的展开图的情况可知有两种情况,
(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.
【解答】解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
【点评】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
20.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
【解答】解:(1)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,
∴∠BAC=45°.
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,
∴△A′B′C′为等腰直角三角形.
∴∠B′A′C′=45°.
∴∠BAC与∠B′A′C′相等.
【点评】本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: A′B′,D′C′,DC ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
【分析】(1)根据长方体的特征填写即可;
(2)根据长方体的表面积公式即可求解;
(3)①根据长方体的表面积公式和正方形的面积公式即可求解;
②分成2个边长40cm的正方形,4个长40cm,宽20cm的长方形即可求解.
【解答】解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
【点评】考查了几何体的展开图,认识立体图形和几何体的表面积,本题考法较新颖,需要对长方体有充分的理解.
22.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方形的表面积.
【分析】(1)根据长方体的展开图判断出多余一个正方形;
(2)根据长方形和正方形的面积公式分别列式计算即可得解.
【解答】解:(1)多余一个正方形如图所示:
2)表面积=52×2+8×5×4
=50+160
=210cm2.
故答案为210cm2.
【点评】本题考查了几何体的展开图以及长方体的表面积的求法,熟练掌握长方体的展开图是解题的关键.
23.图中,
(1)请直接写出图1和图2几何体的名称,
(2)图3和图4是某些几何体的平面展开图,请判断后在横线上写出相应的几何体的名称.
【分析】(1)利用立体图形的特征求解即可,
(2)利用立体图形的展开图特征求解即可.
【解答】解:(1)由立体图形的特征可得图
1和图2分别为正方体,长方体,
(2)由立体图形的展开图特征可得图
3和图4相应的几何体分别为正四棱锥,三棱柱,
【点评】本题主要考查了几何体的展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
24.(2015秋 江都区校级月考)如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
【分析】(1)把展开图折叠成一个长方体,找到与F重合的点即可;
(2)设长方体的长、宽、高分别为x、y、z,根据题意可知:2z+y=4z,x=3z,2x+2z﹣(2z+2y)=8,从而可求得x、y、z的值,从而可求得元长方体的容积.
【解答】解:(1)与F重合的点是B.
(2)设长方体的长、宽、高分别为x、y、z.
根据题意得:
解得:.
∴原长方体的容积=4×8×12=384.
【点评】本题主要考查的是展开图折叠成几何体,根据题意列出方程组是解题的关键.
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
【分析】根据折叠情况,即可画出图形.
【解答】解:如图所示:
【点评】本题考查了学生对几何体的展开图的理解,以及空间想象能力.
26.(2013秋 相城区期末)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 100cm2 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= h(a﹣2h)2cm3 ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 432cm3 .
【分析】(1)根据已知得出长方体底面的边长进而求出即可;
(2)利用底面积乘高得出无盖长方体盒子的容积即可;
(3)根据材料一定长方体中体积最大与底面积和高都有关,进而得出答案.
【解答】解:(1)∵a=18cm,h=4cm,
∴这个无盖长方体盒子的底面面积为:(a﹣2h)(a﹣2h)=(18﹣2×4)×(18﹣2×4)=100(cm2);
故答案为:100cm2;
(2)这个无盖长方体盒子的容积V=h(a﹣2h)(a﹣2h)=h(a﹣2h)2(cm3);
故答案为:h(a﹣2h)2cm3;
(3)若a=18cm,当h越大,无盖长方体盒子的容积V不一定就越大
展开与折叠
一.选择题
1.如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇
B.见
C.未
D.来
2.如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
3.下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
5.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
6.有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白
B.红
C.黄
D.黑
7.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
8.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
9.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
10.如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
A.
B.
C.
D.
二.填空题
11.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
12.如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2﹣ab﹣ac﹣bc的值为 .
13.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 种拼接方法.
14.一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是 .
15.如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是 .
三.解答题
16.将图中剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去几号小正方形?写出所有可能的情况.
17.如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
18.如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
19.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
20.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
22.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方形的表面积.
23.图中,
(1)请直接写出图1和图2几何体的名称,
(2)图3和图4是某些几何体的平面展开图,请判断后在横线上写出相应的几何体的名称.
24.如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
26.如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 .
参考答案与解析
一.选择题
1.(2016 达州)如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )
A.遇
B.见
C.未
D.来
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“遇”与“的”是相对面,
“见”与“未”是相对面,
“你”与“来”是相对面.
故选D.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2016 资阳)如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A.
B.
C.
D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴C符合题意.
故选C.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.(2016 徐州)下列图形中,不可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
【分析】利用不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况进行判断也可.
【解答】A.可以作为一个正方体的展开图,
B.可以作为一个正方体的展开图,
C.不可以作为一个正方体的展开图,
D.可以作为一个正方体的展开图,
故选;C.
【点评】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.(2016 绍兴)如图是一个正方体,则它的表面展开图可以是( )
A.
B.
C.
D.
【分析】根据含有田字形和凹字形的图形不能折成正方体可判断A、C,D,故此可得到答案.
【解答】解:A、含有田字形,不能折成正方体,故A错误;
B、能折成正方体,故B正确;
C、凹字形,不能折成正方体,故C错误;
D、含有田字形,不能折成正方体,故D错误.
故选:B.
【点评】本题主要考查的是几何体的展开图,明确含有田字形和凹字形的图形不能折成正方体是解题的关键.
5.(2016 河北)图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.
【解答】解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,故选:A.
【点评】本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.
6.(2016 枣庄)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
A.白
B.红
C.黄
D.黑
【分析】根据图形可得涂有绿色一面的邻边是白,黑,红,蓝,即可得到结论.
【解答】解:∵涂有绿色一面的邻边是白,黑,红,蓝,
∴涂成绿色一面的对面的颜色是黄色,
故选C.
【点评】本题考查了正方体相对两个面上的文字问题,此类问题可以制作一个正方体,根据题意在各个面上标上图案,再确定对面上的图案,可以培养动手操作能力和空间想象能力.
7.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点.
【解答】解:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图案的位置正好相反,所以能得到的图形是C.
故选C.
【点评】考查了几何体的展开图,解决此类问题,要充分考虑带有各种符号的面的特点及位置.
8.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
【分析】根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【解答】解:∵三棱柱展开图有3个四边形,2个三角形,
∴C选项不是三棱柱展开图,
故选:C.
【点评】本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
9.如图,将长方体表面展开,下列选项中错误的是( )
A.
B.
C.
D.
【分析】长方体的表面展开图的特点,有四个长方形的侧面和上下两个底面组成.
【解答】解:A、是长方体平面展开图,不符合题意;
B、是长方体平面展开图,不符合题意;
C、有两个面重合,不是长方体平面展开图,不符合题意;
D、是长方体平面展开图,不符合题意.
故选:C.
【点评】本题考查的是长方体的展开图,关键是要注意上下底面的长和宽是否可以围成长方体.
10.如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
A.
B.
C.
D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:选项A、C、D折叠后都不符合题意,只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去三角形交于一个顶点符合.
故选:B.
【点评】考查了截一个几何体和几何体的展开图.解决此类问题,要充分考虑带有各种符号的面的特点及位置.
二.填空题
11.(2016 云南)如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
12.如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2﹣ab﹣ac﹣bc的值为 76 .
【分析】本题须先求出a﹣b=﹣4,b﹣c=﹣6,c﹣a=10,再通过对要求的式子进行化简整理,代入相应的值即可求出结果.
【解答】解:∵正方体的每一个面上都有一个正整数,相对的两个面上两数之和都相等,
∴a+13=b+9=c+3,
∴a﹣b=﹣4,b﹣c=﹣6,c﹣a=10,
a2+b2+c2﹣ab﹣bc﹣ca=
=
=
=76
故答案为:76.
【点评】本题主要考查了整式的混合运算﹣化简求值问题,在解题时要注意知识的综合运用及与图形结合问题.
13.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 4 种拼接方法.
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【解答】解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
【点评】此题主要考查了几何体的展开图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
14.一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是 碳 .
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“低”与“绿”是相对面,
“碳”与“保”是相对面,
“环”与“色”是相对面.
故答案为:碳.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
15.如图所示的平面纸能围成正方体盒子,请把与面A垂直的面用图中字母表示出来是 B、C、E、F .
【分析】根据正方体展开图的11种特征,本题属于正方体展开图的“141”结构,把它折成正方体后,A面与D面相对,其余的面都与A面垂直.
【解答】解:因为正方体的表面展开图,相对的面之间一定相隔一个正方形,面“A”与“D”是相对面,它们互相平行,剩下的面都与A面垂直;
所以:围成正方体盒子,与面A垂直的面用图中字母表示出来是:B、C、E、F;
故答案为:B、C、E、F.
【点评】本题考查了展开图折叠成几何体,注意正方体的空间图形,从相对面入手,分析及解答问题.
三.解答题
16.将图中剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去几号小正方形?写出所有可能的情况.
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:根据有“田”字格的展开图都不是正方体的表面展开图可知:应剪去1或2或3.
【点评】此题主要考查了正方体展开图,关键是掌握正方体展开图的特点,中间四联方,上下各一个.
17.如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
【分析】此题的关键是找出正方体的相对面,仔细观察会发现3与x是相对面,3﹣2y与y是相对面,z+4与1﹣2x是相对面,根据这个正方体纸盒相对的两个面上的代数式的值相等,求出x,y,z的值.
【解答】解:根据题意得:
解得:.
【点评】考查了正方体相对两个面上的文字,做这类题学生要养成仔细观察并动脑的习惯.
18.如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
【分析】(1)根据几何体的三视图,可得出几何体是六棱柱;
(2)由图可得侧面积等于六个矩形的面积.
【解答】解:(1)这个几何体的名称是六棱柱;
(2)侧面积=(2+4)ab=6ab.
【点评】本题考查了由三视图判断几何体以及几何体的表面积,几何体的侧面积等于六个矩形的面积.
19.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 8 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
【分析】(1)根据平面图形得出剪开棱的条数,
(2)根据长方体的展开图的情况可知有两种情况,
(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.
【解答】解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
【点评】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
20.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
【分析】(1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
【解答】解:(1)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,
∴∠BAC=45°.
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=,B'C'=.
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,
∴△A′B′C′为等腰直角三角形.
∴∠B′A′C′=45°.
∴∠BAC与∠B′A′C′相等.
【点评】本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.
21.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
(1)写出与棱AB平行的所有的棱: A′B′,D′C′,DC ;
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
【分析】(1)根据长方体的特征填写即可;
(2)根据长方体的表面积公式即可求解;
(3)①根据长方体的表面积公式和正方形的面积公式即可求解;
②分成2个边长40cm的正方形,4个长40cm,宽20cm的长方形即可求解.
【解答】解:(1)与棱AB平行的所有的棱:A′B′,D′C′,DC.
故答案为:A′B′,D′C′,DC;
(2)长方体的表面积=2a2+4ab;
(3)①当a=40cm,b=20cm时,
2a2+4ab
=2×402+4×40×20
=3200+3200
=6400(cm2)
∵c2=2a2+4ab=6400,
∴c=80(
cm
);
②如下图所示:(注:答案不唯一,只要符合题意画一种即可)
【点评】考查了几何体的展开图,认识立体图形和几何体的表面积,本题考法较新颖,需要对长方体有充分的理解.
22.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方形的表面积.
【分析】(1)根据长方体的展开图判断出多余一个正方形;
(2)根据长方形和正方形的面积公式分别列式计算即可得解.
【解答】解:(1)多余一个正方形如图所示:
2)表面积=52×2+8×5×4
=50+160
=210cm2.
故答案为210cm2.
【点评】本题考查了几何体的展开图以及长方体的表面积的求法,熟练掌握长方体的展开图是解题的关键.
23.图中,
(1)请直接写出图1和图2几何体的名称,
(2)图3和图4是某些几何体的平面展开图,请判断后在横线上写出相应的几何体的名称.
【分析】(1)利用立体图形的特征求解即可,
(2)利用立体图形的展开图特征求解即可.
【解答】解:(1)由立体图形的特征可得图
1和图2分别为正方体,长方体,
(2)由立体图形的展开图特征可得图
3和图4相应的几何体分别为正四棱锥,三棱柱,
【点评】本题主要考查了几何体的展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
24.(2015秋 江都区校级月考)如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
【分析】(1)把展开图折叠成一个长方体,找到与F重合的点即可;
(2)设长方体的长、宽、高分别为x、y、z,根据题意可知:2z+y=4z,x=3z,2x+2z﹣(2z+2y)=8,从而可求得x、y、z的值,从而可求得元长方体的容积.
【解答】解:(1)与F重合的点是B.
(2)设长方体的长、宽、高分别为x、y、z.
根据题意得:
解得:.
∴原长方体的容积=4×8×12=384.
【点评】本题主要考查的是展开图折叠成几何体,根据题意列出方程组是解题的关键.
25.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
【分析】根据折叠情况,即可画出图形.
【解答】解:如图所示:
【点评】本题考查了学生对几何体的展开图的理解,以及空间想象能力.
26.(2013秋 相城区期末)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.
(1)若a=18cm,h=4cm,则这个无盖长方体盒子的底面面积为 100cm2 ;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V= h(a﹣2h)2cm3 ;
(3)若a=18cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是 432cm3 .
【分析】(1)根据已知得出长方体底面的边长进而求出即可;
(2)利用底面积乘高得出无盖长方体盒子的容积即可;
(3)根据材料一定长方体中体积最大与底面积和高都有关,进而得出答案.
【解答】解:(1)∵a=18cm,h=4cm,
∴这个无盖长方体盒子的底面面积为:(a﹣2h)(a﹣2h)=(18﹣2×4)×(18﹣2×4)=100(cm2);
故答案为:100cm2;
(2)这个无盖长方体盒子的容积V=h(a﹣2h)(a﹣2h)=h(a﹣2h)2(cm3);
故答案为:h(a﹣2h)2cm3;
(3)若a=18cm,当h越大,无盖长方体盒子的容积V不一定就越大
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
